Выполнение работы. 1.Для определения увеличения микроскопа применяют объект микрометры, представляющие собой шкалу с известной ценой деления
1.Для определения увеличения микроскопа применяют объект микрометры, представляющие собой шкалу с известной ценой деления, нанесенную на прозрачную стеклянную пластинку. Обычно цена деления объект микрометра 0, 01 мм. На расстоянии 25 см от окуляра микроскопа перпендикулярно оптической оси микроскопа устанавливается масштабная линейка. При наблюдении вдоль оптической оси изображение масштабной линейки попадает в глаз наблюдателя и совмещается с изображением объект микрометра. Пусть число делений Отсюда для увеличения микроскопа получим 2. Измерить микрометром толщину стеклянной пластинки d. Поместить пластинку на столик микроскопа и сфокусировать его на метку, расположенную на верхней стороне пластинки. 3. Медленно вращая микрометрический винт определить расстояние 4. Сфокусировать микроскоп на метку находящуюся на предметном стекле микроскопа. Накрыть метку исследуемой пластинкой. Медленно вращая микрометрический винт определить расстояние «х» на которое надо поднять тубус микроскопа для того, чтобы снова сфокусировать его на метку. 5. По формулам 7.3, 8.3 и 9.3 определить показатель преломления стекла. Сравнить полученные результаты.
Контрольные вопросы. 1. Законы преломления света. Абсолютный и относительный показатель преломления. 2. Глаз. Оптические приборы. 3. Ход лучей в микроскопе. 4. Почему с использованием видимого света невозможно получить увеличение больше 2000? 5. Выведите формулы /7.3/ и /8.3/.
РАБОТА № 4
ОПРЕДЕЛЕНИЕ РАДИУСА КРИВИЗНЫ ЛИНЗЫ С ПОМОЩЬЮ КОЛЕЦ НЬЮТОНА
Цель работы: изучение интерференции света и определение радиуса кривизны линзы.
Принадлежности: микроскоп, плосковыпуклая линза, стеклянная пластина.
Краткая теория Явление наложения двух когерентных волн приводящее к образованию устойчивой картины распределения максимумов и минимумов получило название интерференции света. Интерферировать могут только когерентные волны. Когерентными называются волны, имеющие одну и ту же длину волны и постоянную во времени разность фаз. Этому условию удовлетворяют монохроматические волны – неограниченные в пространстве волны одной строго определенной частоты и постоянной амплитуды. Поскольку ни один реальный источник света не дает монохроматического света, волны, излучаемые двумя независимыми источниками света, всегда некогерентные. Поэтому на опыте нельзя наблюдать интерференцию света от двух источников. На практике для наблюдения интерференции световых волн применяют метод разделения световой волны, излучаемой одним источником на две части, которые после прохождения различных оптических путей накладываются друг на друга и дают интерференционную картину. Пусть разделение волны на две части происходит в точке О. До точки М, в которой наблюдается интерференционная картина, одна волна в среде с показателем преломления Результат интерференции определяется разностью фаз интерферирующих волн в точке наблюдения. Пусть в точке О фаза колебаний равна Разность фаз двух интерферирующих волн от одного источника будет равна:
Так как Произведение геометрической длины S пути световой волны в данной среде на показатель преломления n этой среды называется оптическим ходом волны L. Тогда разность фаз Если оптическая разность хода волн равна целому числу длин волн
то
то в точке М наблюдается интерференционный минимум. Создание интерференционной картины световых волн от одного источника можно достичь путем амплитудного разделения каждого луча на границе раздела сред. Такое разделение можно осуществить путем отражения света от поверхностей тонкого прозрачного слоя (рис.1). Лучи 1 и 2 интерферируют между собой, являясь когерентными как части одного луча. При этом если углы Мы уже указывали, что условие интерференционного минимума имеет вид: У поверхности клина для толщины, удовлетворяющей условию 2.4 образуются темные интерференционные полосы (полосы равной толщины) параллельные ребру клина.
Параллельный пучок лучей падает нормально на плоскую поверхность линзы и частично отражается от верхней и нижней поверхностей воздушного (n = 1) зазора между линзой и пластиной. При наложении отраженных волн возникают полосы равной толщины, имеющие вид концентрических окружностей с темным пятном в центре (кольца Ньютона). Определим радиус Тогда Используя условие интерференционного минимума 4.2 можно получить
где m = 1, 2, 3, ……… порядковый номер кольца. Формула 4.3 позволяет исследовать явление интерференции в тонких пленках, а также определить радиус кривизны поверхности линзы. Однако из-за плохого контакта линзы с пластиной, использование этой формулы для целей указанных выше, дает большие погрешности. Целесообразнее использовать формулу:
Выполнения работы. Наблюдение и измерение колец Ньютона производится в отраженном свете с помощью микроскопа. На столике микроскопа установлена стеклянная пластина, а на ней напротив объектива – исследуемая линза. 1. Включить осветитель. Найти кольца Ньютона и добиться их хорошей видимости. 2. Вращая барабан микрометрического винта, установить визирную линию на середину последнего наблюдаемого темного кольца Ньютона влево от центра и производят отсчет показаний по шкале и барабану. 3. Вращая барабан окулярного микрометра, наводят визирную линию на последующие кольца и производят аналогичные отсчеты. 4.Пройдя центральное темное пятно, производят измерение для тех же колец справа от центра. Так как ближайшие к центральному пятну несколько колец обычно бывают сильно размыты, что затрудняет установку на них визирной линии, то измерение их можно не производить. Результаты измерений занести в таблицу 1. Используя полученные данные по формуле 4.4 определить радиус кривизны поверхности линзы. = 650 нм Таблица 1.
Контрольные вопросы. 1. Что такое интерференция волн? 2. Какие волны называются когерентными? 3. Интерференционные полосы равной толщины и равного наклона. 4. Объясните образование колец Ньютона. Выведите рабочую формулу. 5. Почему нельзя получить интерференционную картину от двух независимых источников света, например, от двух электрических ламп?
РАБОТА № 5.
ОПРЕДЕЛЕНИЕ ДЛИНЫ СВЕТОВОЙ ВОЛНЫ С ПОМОЩЬЮ ДИФРАКЦИОННОЙ РЕШЕТКИ
Цель работы: изучение явления дифракции и определение длины световой волны.
Принадлежности: Дифракционная решетка, лазер, оптическая скамья.
Краткая теория Дифракцией называется явление огибания волнами препятствий, встречающихся на их пути, или в более широком смысле – любое отклонение при распространении волн от законов геометрической оптики. На опыте явление дифракции наблюдается только в том случае, если размеры препятствий или отверстий сравнимы с длиной волны. Благодаря дифракции волны могут попадать в область геометрической тени, огибать препятствия, проникать через небольшие отверстия и т.д. Явление дифракции объясняется с помощью принципа Гюйгенса, согласно которому каждая точка среды, до которой доходит волна, становится источником вторичных волн, а огибающая этих вторичных волн дает положение волнового фронта в следующий момент времени.
Принцип Гюйгенса, являясь чисто геометрическим способом построения волновой поверхности, решает лишь задачу о направлении распространения волны, но не затрагивает вопроса об амплитуде, а, следовательно, и об интенсивности волн, распространяющихся в различных направлениях. Френель вложил в принцип Гюйгенса физический смысл, дополнив его идеей об интерференции вторичных волн. Согласно Френелю, любая световая волна, возбуждаемая источником света, может быть представлена как результат интерференции вторичных волн. Учет амплитуд и фаз вторичных волн позволяет в каждом конкретном случае найти амплитуду результирующей волны в каждой точке пространства, т.е. определить закономерности распространения света.
Рассмотрим дифракцию света на бесконечно длинной щели. Пусть плоская монохроматическая волна падает нормально на бесконечную щель шириной а (рис. 2). Оптическая разность хода между крайними лучами, распространяющимися от щели под углом
Разобьем щель на зоны Френеля, имеющие вид полос, параллельных ребру щели. Ширина зоны выбирается таким образом, чтобы разность хода лучей от краев этих зон была равна
Из выражения 5.2 вытекает, что число зон Френеля зависит от угла Следовательно, если число зон четное, то наблюдается дифракционный минимум. Условия наблюдения минимума можно записать в виде
Если же число зон нечетное, то в точке наблюдения будет максимум, соответствующий действию одной зоны Френеля. В прямом направлении Из условия 5.3 можно определить направления на точки экрана, в которых амплитуда (а, следовательно, и интенсивность) колебаний равна нулю Распределение интенсивности света на экране, получаемое вследствие дифракции, показано на рис. Положение дифракционных максимумов и минимумов зависит от длины волны Большое практическое значение имеет дифракция, наблюдаемая при прохождении света через одномерную дифракционную решетку – систему параллельных щелей равной ширины, лежащих в одной плоскости и разделенных равными по ширине непрозрачными участками.
Пусть на дифракционную решетку нормально падает плоская монохроматическая волна (рис. 5.3). В точке С будет происходить интерференция лучей, идущих не только от различных зон одной и той же щели, но и интерференция лучей идущих от соответствующих зон двух щелей. Разность хода лучей, идущих от двух щелей, для данного направления
Ранее мы показали, что распределение интенсивности на экране определяется только направлением дифрагирующих лучей. Это означает, что перемещение щели вправо или влево параллельно самой себе не изменяет дифракционной картины. Очевидно, что в тех направлениях, в которых ни одна из щелей не посылает света, он не будет распространяться и при двух щелях, т.е. главные минимумы интенсивности будут наблюдаться в направлении, определяемым условием:
Кроме того, вследствие интерференции лучей посылаемых двумя щелями в некоторых направления будут возникать дополнительные минимумы. Этим направлениям соответствует разность хода волн
В направлениях удовлетворяющих условию
будут наблюдаться главные максимумы. Другими словами при двух щелях между двумя главными максимума располагается один дополнительный минимум. Если дифракционная решетка состоит из N щелей, то условие главных минимумов и максимумов не изменяются, а условие дополнительных минимумов имеет вид
Так как модуль
определяется отношением периода дифракционной решетки к длине световой волны. Положение дифракционного максимума зависит от длины волны
Выполнение работы. В данной работе лазерное излучение падает на дифракционную решетку ( На экране наблюдается ряд дифракционных максимумов в виде пятен, убывающих по интенсивности от центра к периферии. Дифракционный угол
Ширину дифракционного максимума
1. Закрепить на экране лист чистой бумаги. 2. Измерить расстояние L от дифракционной решетки до экрана. 3. Включить лазер. 4. На листе бумаги зарисовать пятна дифракционных максимумов. 5. Измерить расстояние между центральным максимумом и максимумами 1, 2, 3, 4 – порядков. По формуле 10.5 рассчитать длину световой волны. Сравнить полученный результат с теоретическим значением. 6. Измерить ширину центрального максимума и по формуле 11.5 определите число щелей дифракционной решетки. Результаты измерений и расчетов занести в таблицу. Таблица 1.
7. Сделать вывод.
Контрольные вопросы. 1. Что такое дифракция света? 2. Сформулируйте принцип Гюйгенса – Френеля. 3. Выведите условия максимумов и минимумов при дифракции от одной щели. 4. Объясните закон прямолинейного распространения света. 5. Объясните, почему при использовании белого света дифракционные максимумы становятся цветными? Почему при этом центральный максимум остается белым?
РАБОТА № 6.
ДИФРАКЦИЯ СВЕТА НА ДВУМЕРНОЙ РЕШЕТКЕ (СЕТКЕ)
Цель работы: Изучение дифракции света на двумерной дифракционной решетке. По полученной дифракционной картине определяются и сравниваются параметры двух решеток. Оборудование: полупроводниковый лазер с длиной волны
Выполнение работы.
Узкий пучок монохроматического света, пройдя через первую решетку с вертикальными штрихами, должен дать совокупность максимумов вдоль горизонтальной оси (см. работу № 5), положение которых определяется из условия
Каждый луч, соответствующий этим максимума, проходя через вторую решетку, распадается на совокупность лучей, дающих дифракционные максимумы вдоль вертикальной оси. Положение этих максимумов определяется выражением
то по найденным значениям
1. Закрепить на экране лист чистой бумаги. 2. Измерить расстояние L от сетки до экрана. 3. Включить установку. 4. На листе бумаги карандашом аккуратно отметить положение максимумов дифракционной картины. 5. Провести через центральный максимум оси координат и измерить расстояние от центрального максимума до максимумов 1, 2, 3, 4, и 5 порядка. Результаты измерений занести в таблицу 1. Опыт повторить с другой решеткой. По формулам 6.4 определить параметры Таблица 1. L =
РАБОТА № 7
ПРОВЕРКА ЗАКОНА МАЛЮСА
Цель работы: изучение явления поляризации света и проверка закона Малюса. Оборудование: оптическая скамья, полупроводниковый лазер, поляризатор и анализатор, фотоприемное устройство с измерителем мощности лазерного излучения.
Краткая теория
Естественный свет можно преобразовать в плоско поляризованный, используя так называемые поляризаторы, пропускающие колебания только одного, строго определенного направления. В качестве поляризаторов могут использоваться среды, анизотропные в отношении колебаний вектора Е, например, кристаллы турмалина. Направим естественный свет перпендикулярно пластинке турмалина, вырезанной параллельно оптической оси кристалла (рис. 3). Вращая эту пластинку вокруг направления луча, никаких изменений интенсивности прошедшего луча мы не обнаружим. Если же на пути луча, вышедшего из первой пластинки, поставить вторую такую пластинку, то при ее вращении интенсивность света, прошедшего через две пластинки меняется в зависимости от угла
где Результаты этого опыта объясняются довольно просто. Первая пластинка турмалина пропускает колебания только одного направления, совпадающего с направлением оптической оси, т.е. преобразует естественный свет в плоско поляризованный. Вторая же пластинка турмалина в зависимости от ее ориентации из поляризованного света пропускает большую или меньшую его часть. Пластинка, преобразующая естественный свет в поляризованный, получила название поляризатора. Вторая пластинка, служащая для анализа степени поляризации света, называется анализатором.
Выполнение работы
1. Включить установку. 2. Вращая анализатор, снимите зависимость показаний измерителя мощности излучения от угла поворота Таблица 1.
3. Постройте график зависимости 4. Сделайте вывод.
РАБОТА № 8
ОПРЕДЕЛЕНИЕ КОНЦЕНТРАЦИИ РАСТВОРА САХАРА МЕТОДОМ ПОЛЯРИЗАЦИОННОГО САХАРИМЕТРА
Цель работы: изучение явления поляризации света и определение концентрации раствора сахара.
Принадлежности: поляризационный сахариметр, набор кювет, растворы сахара различной концентрации. Краткая теория
В основе работы поляризационных приспособлений, служащих для получения поляризованного света и использования его в технических целях, лежит явление двойного лучепреломления. Для того, чтобы поляризованный свет можно было использовать на практике необходимо обыкновенный и необыкновенный лучи пространственно разделить как можно дальше. Наиболее широкое применение нашла призма Николя или просто николь. Кристалл исландского шпата разрезают через его тупые углы, а затем склеивают канадским бальзамом (рис. 8.2). Поэтому обыкновенный луч
Опыт показывает, что для кристаллических тел и чистых жидкостей
где Для растворов оптически активных веществ эта формула имеет вид:
где С – концентрация вещества в растворе. Явление вращения плоскости поляризации и, в частности, формула 8.2 лежит в основе точного метода определения концентрации раствора оптически активного вещества.
Выполнения работы. В данной работе используется поляризационный сахариметр. Два николя расположены в концах металлической трубки, а между ними помещается кювета с исследуемым раствором. На первый николь падает естественный луч света. Второй николь с помощью винта может вращаться вокруг оси прибора. Угол поворота второго николя с помощью нониуса отсчитывается по шкале. Установить николи в положение скрещивания по наблюдению изменения интенсивности прошедшего через николи света очень сложно. Поэтому, для повышения точности измерений, в сахариметр вводят дополнительные оптические элементы. Поле зрения в таком сахари
|

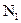 объект микрометра укладывается на число делений
объект микрометра укладывается на число делений 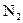 масштабной линейки. Тогда, если цена деления объект микрометра равна а, а масштабной линейки b, то выполняется условие:
масштабной линейки. Тогда, если цена деления объект микрометра равна а, а масштабной линейки b, то выполняется условие:  .
.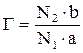 .
. , на которое надо опустить тубус микроскопа для фокусировки на нижнюю метку.
, на которое надо опустить тубус микроскопа для фокусировки на нижнюю метку.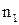 проходит путь
проходит путь  , а вторая в среде с показателем преломления
, а вторая в среде с показателем преломления 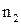 - путь
- путь 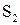 .
.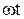 . Тогда в точке М фаза первой волны
. Тогда в точке М фаза первой волны 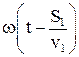 , а второй
, а второй 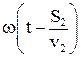 , где
, где 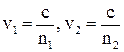 - фазовые скорости первой и второй волны.
- фазовые скорости первой и второй волны.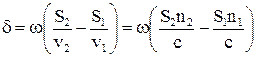
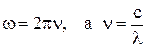 и получим
и получим 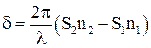
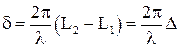 , где
, где 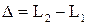 - оптическая разность хода волн.
- оптическая разность хода волн.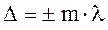 , 1.4
, 1.4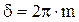 и колебания, возбуждаемые в точке М обеими волнами, находятся в одной фазе и, следовательно, условие /1/ является условием наблюдения интерференционного максимума. Если выполняется условие
и колебания, возбуждаемые в точке М обеими волнами, находятся в одной фазе и, следовательно, условие /1/ является условием наблюдения интерференционного максимума. Если выполняется условие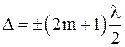 , 2.4
, 2.4 и i являются малыми, то интерференционная картина лежит вблизи поверхности клина. Оптическая разность хода для этих лучей определяется в виде
и i являются малыми, то интерференционная картина лежит вблизи поверхности клина. Оптическая разность хода для этих лучей определяется в виде 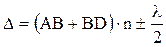 . Полагая (для малых углов), что
. Полагая (для малых углов), что 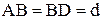 получим для разности хода выражение
получим для разности хода выражение  где d – толщина клина в месте наблюдения, n – показатель преломления материала клина. Дополнительная разность хода
где d – толщина клина в месте наблюдения, n – показатель преломления материала клина. Дополнительная разность хода 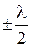 возникает в результате потери полуволны при отражении от оптически более плотной среды. Знак (+) или (-) берется в зависимости от того в какой точке происходит указанное отражение. Если потеря полуволны происходит в точке А, то берется знак (-), если в точке В, то (+).
возникает в результате потери полуволны при отражении от оптически более плотной среды. Знак (+) или (-) берется в зависимости от того в какой точке происходит указанное отражение. Если потеря полуволны происходит в точке А, то берется знак (-), если в точке В, то (+).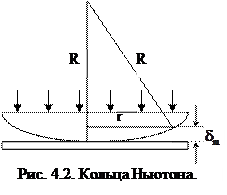 Классическим примером полос равной толщины являются кольца Ньютона, наблюдающиеся при отражении света от тонкого воздушного клина, образованного плоскопараллельной пластиной и соприкасающейся с ней плосковыпуклой линзой с большим радиусом кривизны (рис.4.2).
Классическим примером полос равной толщины являются кольца Ньютона, наблюдающиеся при отражении света от тонкого воздушного клина, образованного плоскопараллельной пластиной и соприкасающейся с ней плосковыпуклой линзой с большим радиусом кривизны (рис.4.2). темного кольца Ньютона. Из рисунка видно, что оптическая разность хода лучей равна (при n = 1)
темного кольца Ньютона. Из рисунка видно, что оптическая разность хода лучей равна (при n = 1) 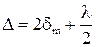 , где
, где 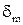 - толщина воздушного зазора. Из рисунка
- толщина воздушного зазора. Из рисунка  .
.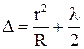 .
. отсюда для радиуса темных колец Ньютона в отраженном свете получим
отсюда для радиуса темных колец Ньютона в отраженном свете получим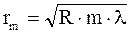 , 3.4
, 3.4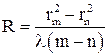 . 4.4
. 4.4 Рассмотрим пример. Когда плоский волновой фронт доходит до преграды с отверстием (рис. 5.1), каждая точка отверстия становится источником вторичных волн, а огибающая этих волн задает фронт волны в последующие моменты времени. Из рисунка видно, что этот фронт плоский только в средней части, а у границ отверстия происходит загибание волнового фронта, т.е. волна попадает в область геометрической тени.
Рассмотрим пример. Когда плоский волновой фронт доходит до преграды с отверстием (рис. 5.1), каждая точка отверстия становится источником вторичных волн, а огибающая этих волн задает фронт волны в последующие моменты времени. Из рисунка видно, что этот фронт плоский только в средней части, а у границ отверстия происходит загибание волнового фронта, т.е. волна попадает в область геометрической тени.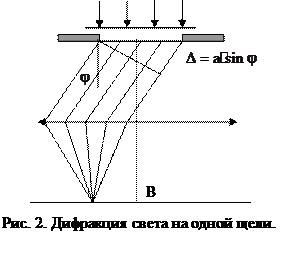 Большое практическое значение имеет дифракция в параллельных лучах или дифракция Фраунгофера. Она наблюдается в том случае, если источник света и точка наблюдения бесконечно удалены от препятствия. Чтобы осуществить этот тип дифракции достаточно источник света поместить в фокусе собирающей линзы, а дифракционную картину наблюдать в фокальной плоскости второй линзы.
Большое практическое значение имеет дифракция в параллельных лучах или дифракция Фраунгофера. Она наблюдается в том случае, если источник света и точка наблюдения бесконечно удалены от препятствия. Чтобы осуществить этот тип дифракции достаточно источник света поместить в фокусе собирающей линзы, а дифракционную картину наблюдать в фокальной плоскости второй линзы.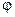 к плоскости щели, будет равна
к плоскости щели, будет равна . 1.5
. 1.5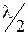 . Тогда на ширине щели укладывается число зон равное
. Тогда на ширине щели укладывается число зон равное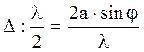 . 2.5
. 2.5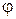 . Но от числа зон зависит результат интерференции всех вторичных волн. Колебания от каждой пары соседних зон Френеля взаимно погашают друг друга, так как они имеют разность фаз равную
. Но от числа зон зависит результат интерференции всех вторичных волн. Колебания от каждой пары соседних зон Френеля взаимно погашают друг друга, так как они имеют разность фаз равную 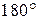 .
.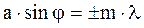 . 3.5
. 3.5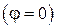 щель действует как одна зона Френеля и в этом направлении свет распространяется с наибольшей интенсивностью и в точке В наблюдается центральный дифракционный максимум.
щель действует как одна зона Френеля и в этом направлении свет распространяется с наибольшей интенсивностью и в точке В наблюдается центральный дифракционный максимум.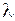 , поэтому рассмотренный вид дифракционной картины имеет место лишь для монохроматического света.
, поэтому рассмотренный вид дифракционной картины имеет место лишь для монохроматического света. Для простоты рассуждений рассмотрим дифракционную решетку, состоящую из двух щелей шириной а, разделенных непрозрачным промежутком шириной b. Величина равная
Для простоты рассуждений рассмотрим дифракционную решетку, состоящую из двух щелей шириной а, разделенных непрозрачным промежутком шириной b. Величина равная 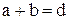 получила название периода (постоянной) дифракционной решетки.
получила название периода (постоянной) дифракционной решетки.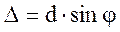 . 4.5
. 4.5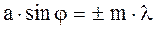 . 5.5
. 5.5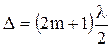 и, следовательно, условие возникновения дополнительных минимумов может быть записано в виде
и, следовательно, условие возникновения дополнительных минимумов может быть записано в виде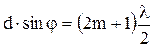 . 6.5
. 6.5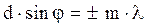 7.5
7.5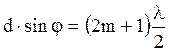 . 8.5
. 8.5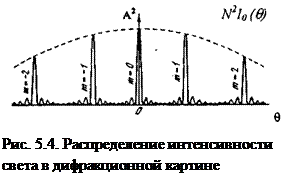 Следовательно, в этом случае между двумя главными максимума располагается (N-1) дополнительный минимум, разделенные вторичными максимумами, создающими слабый фон. Чем больше щелей содержит решетка, тем большее количество световой энергии проходит через нее, тем больше минимумов образуется между двумя главными максимумами, тем более острыми и интенсивными будут максимумы. Распределение интенсивности света в дифракционной картине приведено на рисунке 5.4.
Следовательно, в этом случае между двумя главными максимума располагается (N-1) дополнительный минимум, разделенные вторичными максимумами, создающими слабый фон. Чем больше щелей содержит решетка, тем большее количество световой энергии проходит через нее, тем больше минимумов образуется между двумя главными максимумами, тем более острыми и интенсивными будут максимумы. Распределение интенсивности света в дифракционной картине приведено на рисунке 5.4. не может быть больше единицы, то из выражения 7.5 следует, что число главных максимумов
не может быть больше единицы, то из выражения 7.5 следует, что число главных максимумов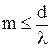 9.5
9.5 . Поэтому при освещении решетки белым светом все максимумы, кроме центрального, разложатся в спектр, фиолетовая часть которого будет обращена к центру дифракционной картины.
. Поэтому при освещении решетки белым светом все максимумы, кроме центрального, разложатся в спектр, фиолетовая часть которого будет обращена к центру дифракционной картины. ). Дифракционная картина наблюдается на экране, удаленном от решетки на расстояние равное
). Дифракционная картина наблюдается на экране, удаленном от решетки на расстояние равное 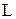 . Расстояние L подбирается так, чтобы выполнялось условие приближения дифракции Фраунгофера.
. Расстояние L подбирается так, чтобы выполнялось условие приближения дифракции Фраунгофера. определяет расстояние
определяет расстояние 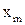 между центральным (нулевым) максимумом и
между центральным (нулевым) максимумом и  ым максимумом. Для малых углов выполняется условие
ым максимумом. Для малых углов выполняется условие 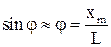 и тогда из 7.5 можно получить
и тогда из 7.5 можно получить . 10.5
. 10.5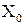 можно оценить с помощью формулы
можно оценить с помощью формулы 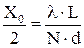 , где
, где 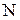 - число щелей дифракционной решетки. Отсюда
- число щелей дифракционной решетки. Отсюда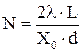 . 11.5
. 11.5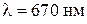 , две сетки с различными параметрами ячеек, линза, экран для наблюдения с магнитами для крепления бумаги.
, две сетки с различными параметрами ячеек, линза, экран для наблюдения с магнитами для крепления бумаги. В данной работе исследуется дифракция лазерного излучения на двумерной дифракционной решетке (сетке). Двумерная решетка представляет собой скрещенные перпендикулярные решетки с периодами
В данной работе исследуется дифракция лазерного излучения на двумерной дифракционной решетке (сетке). Двумерная решетка представляет собой скрещенные перпендикулярные решетки с периодами 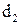 . Подобный случай легко осуществить, нанеся на стеклянную пластинку штрихи, направления которых перпендикулярны друг другу (рис.6.1).
. Подобный случай легко осуществить, нанеся на стеклянную пластинку штрихи, направления которых перпендикулярны друг другу (рис.6.1).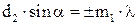 . 1.6
. 1.6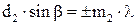 . 2.6
. 2.6  Таким образом, главные максимумы возможны только по направлениям, удовлетворяющим условиям 6.1 и 6.2, причем каждой паре значений целых чисел
Таким образом, главные максимумы возможны только по направлениям, удовлетворяющим условиям 6.1 и 6.2, причем каждой паре значений целых чисел 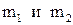 соответствует максимум того или иного порядка. Дифракционная картина в этом случае имеет вид отдельных светлых пятен, интенсивность которых убывает по закону распределения интенсивности в одномерной решетке. Вид картины приведен на рисунке 6.2. Так как в данном случае выполняются условия
соответствует максимум того или иного порядка. Дифракционная картина в этом случае имеет вид отдельных светлых пятен, интенсивность которых убывает по закону распределения интенсивности в одномерной решетке. Вид картины приведен на рисунке 6.2. Так как в данном случае выполняются условия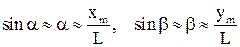 , 3.6
, 3.6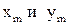 можно определить параметры
можно определить параметры 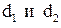 для заданной структуры
для заданной структуры . 4.6
. 4.6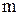

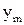
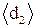
 Поперечность световых волн вытекает непосредственно из теории электромагнетизма Максвелла. Векторы напряженности электрического и магнитного полей взаимно перпендикулярны и колеблются в плоскости перпендикулярной направлению распространения волны (рис. 7.1). Плоскость, в которой происходят колебания вектора Е, называется плоскостью поляризации.
Поперечность световых волн вытекает непосредственно из теории электромагнетизма Максвелла. Векторы напряженности электрического и магнитного полей взаимно перпендикулярны и колеблются в плоскости перпендикулярной направлению распространения волны (рис. 7.1). Плоскость, в которой происходят колебания вектора Е, называется плоскостью поляризации. Световая волна представляет собой суммарное излучение огромного количества атомов. Так как каждый атом излучает свет независимо от других атомов, то в световой волне, излучаемой макроскопическим телом в целом, присутствуют всевозможные равновероятные направления колебаний вектора Е (рис. 7.2 а). Такой свет получил название естественного. Свет, в котором направление колебаний каким-то образом упорядочены, называется поляризованным. Если в результате какого-то внешнего воздействия появляется преимущественное (но не исключительное) направление колебаний вектора Е, то такой свет называется частично поляризованным (рис. 7.2 б). Свет, в котором колебания вектора Е происходят в одной, строго определенной плоскости, называется плоско поляризованным (рис. 7.2 в).
Световая волна представляет собой суммарное излучение огромного количества атомов. Так как каждый атом излучает свет независимо от других атомов, то в световой волне, излучаемой макроскопическим телом в целом, присутствуют всевозможные равновероятные направления колебаний вектора Е (рис. 7.2 а). Такой свет получил название естественного. Свет, в котором направление колебаний каким-то образом упорядочены, называется поляризованным. Если в результате какого-то внешнего воздействия появляется преимущественное (но не исключительное) направление колебаний вектора Е, то такой свет называется частично поляризованным (рис. 7.2 б). Свет, в котором колебания вектора Е происходят в одной, строго определенной плоскости, называется плоско поляризованным (рис. 7.2 в).
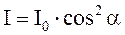 , 1.7
, 1.7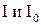 - соответственно интенсивности света, прошедшего через вторую пластинку и падающего на нее. Следовательно, интенсивность прошедшего через пластинки света изменяется от минимума при
- соответственно интенсивности света, прошедшего через вторую пластинку и падающего на нее. Следовательно, интенсивность прошедшего через пластинки света изменяется от минимума при  (полное гашение света) до максимума при
(полное гашение света) до максимума при 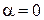 .
. Общая оптическая схема установки представлена на рисунке 7.4 и включает: 1 – полупроводниковый лазер, 2 – поляризатор, 3 – анализатор, закрепленный во вращающейся оправе с измерительным лимбом угла поворота, 4 - фотоприемное устройство с измерителем мощности лазерного излучения.
Общая оптическая схема установки представлена на рисунке 7.4 и включает: 1 – полупроводниковый лазер, 2 – поляризатор, 3 – анализатор, закрепленный во вращающейся оправе с измерительным лимбом угла поворота, 4 - фотоприемное устройство с измерителем мощности лазерного излучения.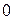
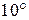
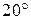
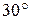
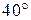
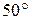


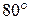
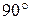
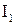

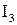
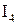
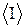
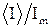
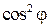
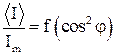 .
. Если на толстый кристалл исландского шпата направить узкий пучок света, то из кристалла выйдут два пространственно разделенных луча, параллельные друг другу и падающему лучу (рис.8.1 а). Даже в том случае, когда луч падает на кристалл нормально, преломленный луч разделяется на два, один из которых является продолжением падающего, а второй отклоняется (рис. 4 б). Второй луч получил название необыкновенного, а первый – обыкновенного. Опыт показывает, что оба луча являются плоско поляризованными, при этом их плоскости поляризации взаимно перпендикулярны.
Если на толстый кристалл исландского шпата направить узкий пучок света, то из кристалла выйдут два пространственно разделенных луча, параллельные друг другу и падающему лучу (рис.8.1 а). Даже в том случае, когда луч падает на кристалл нормально, преломленный луч разделяется на два, один из которых является продолжением падающего, а второй отклоняется (рис. 4 б). Второй луч получил название необыкновенного, а первый – обыкновенного. Опыт показывает, что оба луча являются плоско поляризованными, при этом их плоскости поляризации взаимно перпендикулярны.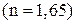 терпит на слое канадского бальзама полное отражение и не выходит из кри
терпит на слое канадского бальзама полное отражение и не выходит из кри  сталла. Необыкновенный луч
сталла. Необыкновенный луч 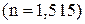 проходит кристалл насквозь. Таким образом, призма Николя дает один плоско параллельный луч. Призма Николя может служит как поляризатором, так и анализатором.
проходит кристалл насквозь. Таким образом, призма Николя дает один плоско параллельный луч. Призма Николя может служит как поляризатором, так и анализатором. Некоторые, так называемые оптически активные вещества, обладают способностью вращать плоскость поляризации. Если между скрещенными поляризатором и анализатором дающими темное поле зрения, поместить оптически активное вещество, то поле зрения анализатора просветляется. При повороте анализатора на некоторый угол
Некоторые, так называемые оптически активные вещества, обладают способностью вращать плоскость поляризации. Если между скрещенными поляризатором и анализатором дающими темное поле зрения, поместить оптически активное вещество, то поле зрения анализатора просветляется. При повороте анализатора на некоторый угол  , 1.8
, 1.8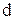 - толщина среды,
- толщина среды, 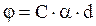 , 2.8
, 2.8


