Применение функции ЛИНЕЙН для множественной регрессии
Для результатов функции ЛИНЕЙН необходимо выделить область пустых ячеек из 5 строк и (p +1) столбцов (p – число факторов). Вызов окна функции ЛИНЕЙН и его заполнение производится так же, как для парной регрессии; отличие состоит в том, что значения x представляют собой диапазон из p строк (или столбцов). Если параметр Статистика установлен в значение 1, то результаты будут выданы, как показано в таблице 7. Результаты функции ЛИНЕЙН для рассматриваемых данных приведены в таблице 8.
Получили следующие оценки коэффициентов множественной регрессии: b 0=-3, 54, b 1=0, 854, b 2=0, 367. Смысл b 1: при увеличении только мощности пласта x 1 на 1 м (при неизменном x 2) добыча угля на 1 рабочего Y возрастет в среднем на 0, 854 усл. ед. Смысл b 2: при увеличении только уровня механизации работ x 2 на 1% (при неизменном x 1) Y возрастет в среднем на 0, 367 усл. ед. Коэффициент b 0 не имеет практического смысла, так как Сравнение регрессионной (QR =27, 27) и остаточной (Qe =6, 33) сумм говорит о значимости уравнения регрессии. Более обоснованное суждение о значимости уравнения можно вынести, используя критерий Фишера. Из таблицы 8 возьмем значение статистики Фишера: F =15, 08. Пороговое значение (квантиль распределения Фишера уровня 1-a с числом степеней свободы k 1= p =2 и k 2= n - p -1=7) определим с помощью функции FРАСПОБР: f (0, 05; 2; 7)=4, 74. Так как статистика F больше порога (неравенство (35) выполнено), то уравнение значимо.
|
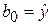при x 1= x 2=0 (см. формулу (27)), а нулевые значения факторов нереальны (далеко отстоят от интервала наблюдений).
