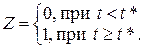Проверка значимости структурных изменений временного ряда

На практике часто встречаются ситуации, когда необходимо сделать вы­бор между непре­рывной и кусочно-линейной моделью времен­ного ряда. На рис. 12 показан пример такой си­туации. Возможно, что надо строить тренд по всем наблюдениям (т.е. ис­пользо­вать непре­рывную модель 1). Но также возможно, что на­блюдения сле­дует разбить на две группы, и оп­ределить свой тренд для каждой группы (т. е. использовать кусочно-линейную модель, со­стоящую из участков 2 и 3). Необходимо при­нять решение о том, какая модель лучше. В эконометрике обычно говорят, что необходимо выявить структурные изменения ряда (или интервен­цию).

Проверим гипотезу Н ₀ о незначимости структурных изменений ряда, т. е. о несущественности различий между кусочно-линейной и непрерывной моделью. Для проверки гипотезы воспользуемся критерием Г. Чоу.

Пусть n – число наблюдений, n ₀ – число наблюдений первой группы, n ₁ – число наблюдений второй группы (n ₀+ n ₁= n); Q ₀ – остаточная сумма при усло­вии, что гипотеза Н ₀ верна (т. е. остаточная сумма непрерывной модели), Q ₁ – остаточная сумма при усло­вии, что гипотеза Н ₀ неверна (т. е. кусочно-линей­ной мо­дели). Сумма Q ₁ складывается из остаточных сумм групп наблюдений.

Далее правило проверки гипотезы Н ₀ строится так же, как в §1.3. Если предположить, что время является единственным фактором модели (p =1), то в соотношениях (48), (49) имеем: k ₁= n -2(p +1)= n -4, k _∆ = p +1=2.

Другой способ выявления структурных изменений ряда состоит в использовании фиктивной переменной. Обозначим t * – момент времени, разделяющий группы наблюдений: при t < t * наблюдение принадлежит первой группе, при t ³ t * – второй (см. рис. 12). В качестве t * можно взять время некоторого события (кризис, забастовка, вливание дополнительных ресурсов), происшедшего между группами наблюдений и способного повлиять на наблюдаемые переменные. Если такое событие неизвестно, то допустимо приблизительно определить t * по графику. Рассмотрим фиктивную переменную Z:

Далее следует рассмотреть регрессионное уравнение (45), оценить коэффициенты m ₁ и b ₁ и определить их значимость.

Заметим, что фиктивные переменные дают возможность более тонкого выявления структурных изменений ряда. Если критерий Г. Чоу только дает ответ «да-нет» на вопрос о значимости структурных изменений, то фиктивные переменные позволяют определить, какой именно параметр уравнения регрессии (коэффициент или сдвиг) претерпел существенные изменения.