Выполнение. Найдем уравнение парной линейной регрессии Y=mX+b по всем наблюдениям таблицы 24 (т
Найдем уравнение парной линейной регрессии Y = mX + b по всем наблюдениям таблицы 24 (т. е. не учитывая качественный признак «Пол студента»). Результаты функции ЛИНЕЙН, необходимые для дальнейших расчетов, приведены в таблице 25. Значение статистики Фишера F =11, 29 больше порога f (0, 05, 1, 10)=4, 96. Таким образом, неравенство (35) справедливо, и уравнение Y =0, 815 X -1, 44 значимо. Следовательно, успеваемость в сессию Y существенно зависит от результатов вступительных экзаменов X. Исследуем влияние пола студента на успеваемость в сессию. Для этого введем фиктивную переменную Z (равную 1 для мужчин и 0 для женщин) и оценим параметры уравнения регрессии Y = mX + m 1 Z + b. Результаты функции ЛИНЕЙН для этого уравнения приведены в таблице 25. Таблица 25. Характеристики уравнений
Значение статистики Фишера F =5, 48 больше порога f (0, 05, 2, 9)=4, 26. Таким образом, уравнение Y =0, 743 X -0, 466 Z -1, 17 значимо, и успеваемость в сессию в основном определяется двумя факторами: результатами вступительных экзаменов и полом студента. Далее надо проверить значимость каждого из этих факторов. Рассчитаем статистики Стьюдента по формуле (36а): Сравнивая значения этих статистик с порогом t (0, 05, 9)=2, 26, получаем, что фактор X значим, а фактор Z незначим (см. формулу (37)). Таким образом, успеваемость студента в сессию в основном зависит от результатов вступительных экзаменов (и слабо зависит от пола студента). Незначимость переменной Z в рассматриваемом уравнении также означает, что пол студента не оказывает значимого влияния на величину сдвига b в уравнении Y = mX + b. Для оценки влияния пола и на коэффициент, и на сдвиг уравнения Y = mX + b надо проанализировать значимость параметров m 1 и b 1 в уравнении (45). В таблицу 24 для работы с уравнением (45) добавим столбец значений ZX. Результаты функции ЛИНЕЙН приведены в таблице 25. Значение статистики Фишера F =3, 31 меньше порога f (0, 05, 3, 8)=4, 07, что говорит о незначимости уравнения. Также оказываются незначимыми все коэффициенты уравнения (это предлагается проверить самостоятельно). По-видимому, двенадцати наблюдений недостаточно для оценивания четырех параметров уравнения. Поэтому для оценки влияния пола на коэффициент уравнения Y = mX + b проверим значимость коэффициента m 1 в уравнении Y = mX + m 1(ZX)+ b; характеристики уравнения представлены в таблице 25. Применяя критерии Фишера и Стьюдента так же, как и для предыдущих уравнений, получим, что уравнение значимо, а коэффициент m 1 незначим. Отсюда можно сделать вывод, что признак «Пол студента» не влияет на коэффициент уравнения регрессии Y = mX + b. Так как признак «Пол студента» не влияет ни на коэффициент, ни на сдвиг уравнения линейной регрессии Y = mX + b, то зависимость Y (Х) одинакова для лиц мужского и женского пола. Этот же вывод можно получить по критерию Г. Чоу (см. §1.3). Если гипотеза H 0 верна (пол студента не влияет на зависимость Y (Х)), то справедливо уравнение Y = mX + b, поэтому Q 0=13, 46, k 0=10. Если H 0 неверна, то зависимость Y от X описывается уравнением (45), поэтому Q 1=12, 80, k 1=8. Из формулы (46) имеем: D Q =0, 663, из (47): k D=2. Подставив эти значения в формулу (48), получим F Чоу=0, 207. Порог для статистики Чоу равен: f (0, 05, 2, 8)=4, 46. Неравенство (49) не справедливо, и гипотеза H 0 не отклоняется. Заметим, что значение остаточной суммы Q 1 можно было получить другим способом. Именно, надо разделить наблюдения на две части: в одну часть отнести наблюдения, для которых Z =0 (женщины), а в другую – для которых Z =1 (мужчины). Далее следует рассчитать остаточные суммы для каждой части (Q 1(Z =0)=2, 19 и Q 1(Z =1)=10, 61) и просуммировать их (получим Q 1=12, 80).
|


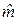 =0, 815
=0, 815
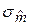 =0, 242
=0, 242
 =0, 466
=0, 466
 =0, 763
=0, 763
 =-0, 952
=-0, 952
 =5, 10
=5, 10
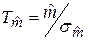 =0, 743/0, 276=2, 69;
=0, 743/0, 276=2, 69;  0, 466/0, 763=0, 611.
0, 466/0, 763=0, 611.


