Проверка незначимости качественного признака по критерию Г. Чоу
Критерий Г. Чоу основывается на сравнении по критерию Фишера остаточных сумм моделей, одна из которых учитывает качественный признак, а другая не учитывает. Пусть n – число наблюдений, Z – двоичная фиктивная переменная, р – число факторов (без фиктивной переменной Z), n 0 – число наблюдений, для которых Z =0, n 1 – число наблюдений, для которых Z =1. Очевидно, что n 0+ n 1= n. Далее, пусть Н 0 – гипотеза о незначимости фиктивной переменной Z, Q 0 – остаточная сумма при условии, что гипотеза Н 0 верна, Q 1 – остаточная сумма при условии, что гипотеза Н 0 неверна. Сумма Q 0 – это остаточная сумма p -факторной линейной регрессии по n наблюдениям, поэтому статистика k 0= n -(p +1). Сумма Q 1 складывается из двух остаточных сумм: Q 1= Q 1(Z =0)+ Q 1(Z =1), где Q 1(Z =0) – остаточная сумма линейной регрессионной модели с p факторами, рассчитанной по n 0 наблюдениям (для которых Z =0); Q 1(Z =1) – остаточная сумма линейной регрессионной модели с p факторами, рассчитанной по n 1 наблюдениям (для которых Z =1). Статистика k 1(Z =0)= n 0-(p +1). Аналогично число степеней свободы для Q 1(Z =1) равно k 1(Z =1)= n 1-(p +1). Число степеней свободы остаточной суммы Q 1 равно k 1= k 1(Z =0)+ k 1(Z =1)= n 0-(p +1)+ n 1-(p +1)= n -2(p +1). Рассмотрим разность: D Q = Q 0- Q 1. (46) Можно доказать, что
где k ∆ = k 0- k 1= p +1. (47) В соответствии с критерием Г. Чоу вычисляется статистика:
которая распределена по Фишеру со степенями свободы k ∆ и k 1. Если гипотеза Н 0 верна, то D Q< < Q 1, ибольшие значения статистики (48) маловероятны. Поэтому гипотезу о незначимости фиктивной переменной Z следует отклонять, если FЧоу> f (a; k ∆ ; k 1), (49) где f (a; k ∆ ; k 1) – квантиль F -распределения уровня 1-a. Вероятность ошибки первого рода (отклонить гипотезу Н 0 при условии, что она верна) для правила (49) равна a. Заметим, что при p =1 сумму Q 1 можно вычислить и как остаточную сумму модели (45) с фиктивными переменными.
|

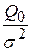 (см. §1.4 практической работы №3) имеет распределение хи-квадрат с числом степеней свободы:
(см. §1.4 практической работы №3) имеет распределение хи-квадрат с числом степеней свободы: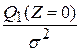 имеет распределение хи-квадрат с числом степеней свободы:
имеет распределение хи-квадрат с числом степеней свободы: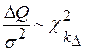 ,
,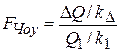 , (48)
, (48)


