Выполнение. Поле корреляции (построенное как точечная диаграмма) показано на рис.13
В таблице 27 представлены оценки уравнений вида Y = mX + b для непрерывной модели и участков кусочно-линейной модели (получены с помощью функции ЛИНЕЙН). Остаточная сумма непрерывной модели (см. §1.4) Q 0=104, 86, ее число степеней свободы k 0=9. Остаточная сумма кусочно-линейной модели получается сложением остаточных сумм линейных участков: Q 1=2, 11+12, 75=14, 86, ее число степеней свободы равно k 1=2+5=7. Из формул (46), (47) имеем: D Q = Q 0- Q 1=104, 86-14, 86=90, D k=k 0- k 1=9-7=2. Подставив эти значения в формулу (48), получим F Чоу=21, 20. Порог для статистики равен f (0, 05, 2, 7)=4, 74. Неравенство (49) справедливо, и гипотеза о незначимости структурных изменений ряда отклоняется. Таким образом, по критерию Г.Чоу зависимость Y (X) до забастовки отличается от зависимости Y (X) после забастовки.
Таблица 27. Характеристики непрерывной и кусочно-линейной моделей
Применим метод фиктивных переменных для анализа значимости структурных изменений ряда. Рассмотрим двоичную переменную:
В таблицу исходных данных добавим две строки: со значениями Z и ZX, и с помощью функции ЛИНЕЙН оценим характеристики уравнения (45); результаты представлены в таблице 28.
Таблица 28. Характеристики уравнения Y = mX + m 1(ZX)+ b 1 Z + b
Заметим, что остаточная сумма этого уравнения равна остаточной сумме кусочно-линейной модели Q 1. Уравнение (45) значимо, так как f (0, 05, 3, 7)=4, 35, и F > f (0, 05, 3, 7). Проверим значимость факторов этого уравнения. Рассчитаем абсолютные значения статистик Стьюдента по формуле (36а): Сравнивая эти значения с порогом t (0, 05, 7)=2, 36, получаем, что факторы X и ZX значимы, а фактор Z незначим (см. формулу (37)). Следовательно, забастовка существенно повлияла на коэффициент уравнения парной линейной регрессии и практически не повлияла на сдвиг. Этот вывод иллюстрируется рис.13, где показаны тренды непрерывной и кусочно-линейной моделей.
|

 Поле корреляции (построенное как точечная диаграмма) показано на рис.13. Видно, что точки наблюдений, соответствующие забастовке (5, 6, 7), являются нетипичными, далеко отстоят от других наблюдений. Поэтому эти точки исключим из дальнейших расчетов.
Поле корреляции (построенное как точечная диаграмма) показано на рис.13. Видно, что точки наблюдений, соответствующие забастовке (5, 6, 7), являются нетипичными, далеко отстоят от других наблюдений. Поэтому эти точки исключим из дальнейших расчетов.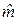




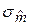


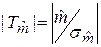 =2, 44/0, 687=3, 56;
=2, 44/0, 687=3, 56;  2, 27/0, 873=2, 60;
2, 27/0, 873=2, 60;  =19, 65/11, 03=1, 78.
=19, 65/11, 03=1, 78.


