Выполнение. Оценим параметры приведенной модели, тОценим параметры приведенной модели, т. е. параметры уравнений регрессии y 1= k 1+ k 2 x 1+ k 3 x 2 и y 2= k 4+ k 5 x 1+ k 6 x 2. С помощью функции ЛИНЕЙН получим: k 1 = 0, 685, k 2 = 0, 852, k 3 = 0, 373, k 4 = 6, 39, k 5 = -0, 072, k 6 = -0, 0056. С помощью несложных алгебраических преобразований можно получить следующие формулы:
Оценим параметры структурной модели двухшаговым МНК. Вычислим оценки
По данным таблицы 33 определить параметры модели формирования равновесных цены и спроса-предложения с учетом тренда дохода. Модель описывается системой одновременных уравнений: Экзогенные переменные модели: Rt – процентная ставка в момент времени t; It – доход в момент времени t; It -1 – доход в момент времени t -1. Эндогенные переменные: Qst – предложение в момент времени t; Qdt – спрос в момент времени t; pt – цена товара в момент времени t.
|
Следовательно, параметры структурной модели однозначно выражаются через параметры приведенной модели, модель идентифицируема и можно применить косвенный МНК. Результаты расчетов по формулам: a 1 = 429, b 1 = -67, g 1 = -4, a 2 = 6, 45, b 2 = -0, 085, g 2 = 0, 026.
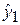и 
откликов по уравнениям приведенной модели – результаты даны в таблице 32. Затем вычислим a 1, b 1, g 1 как параметры регрессии y 1 на 
3. Задание на самостоятельную работу*
