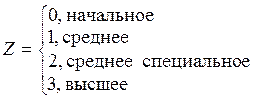Использование фиктивных переменных для анализа значимости качественных признаков в модели пространственной выборки
Фиктивная переменная – это фактор, который принимает дискретные значения. Типичный пример фиктивной переменной – двоичная переменная X, которая равна 0 для мужчин и 1 для женщин. Другой пример:
В данных примерах фиктивная переменная используется для кодирования значений качественного (т. е. нечислового) признака.
Обычно от переменных, принимающих k значений: 0, 1, …, k -1, переходят к двоичным переменным (их число (k -1)). Например, вместо переменной Z следует взять переменные: Переменная Z 4, указывающая на высшее образование, не используется, так как в силу равенства Z 1+ Z 2+ Z 3+ Z 4=1 факторы Z 1, Z 2, Z 3, Z 4 зависимы, и матрица Х в уравнении регрессии (25) при использовании четырех переменных будет вырожденной (в таком случае говорят, что имеет место мультиколлинеарность). Высшее образование кодируется значениями: Z 1= Z 2= Z 3=0. Значимость фиктивной переменной можно, например, проверить, по критерию Стьюдента (см. соотношение (37)). Пусть эконометрическая модель описывается двумя факторами: непрерывным X и дискретным Z, и откликом Y. Переменные Y и X связаны уравнением линейной регрессии (1). Требуется вынести суждение о том, влияет ли значение дискретного признака Z на параметры уравнения регрессии. Для простоты будем считать Z двоичной переменной. Пусть при Z =0 Y = mX + b, а при Z =1 Y = mX + b + m 1 X + b 1. Тогда для произвольного значения Z справедлива формула: Y = mX + b + Z (m 1 X + b 1). После несложных преобразований получим: Y = mX + m 1(ZX)+ b 1 Z + b. (45) Таким образом, для оценивания значимости влияния Z на коэффициент регрессии достаточно по критерию Стьюдента (см. неравенство (37)) проверить гипотезу о незначимости коэффициента m 1 (при новой переменной ZX), а для оценивания влияния Z на сдвиг уравнения линейной регрессии достаточно проверить гипотезу о незначимости b 1 (коэффициента при переменной Z).
|