Приложение. Формулы для выборочных характеристикПусть X и Y – наблюдаемые величины, (x 1, y 1), …, (xn, y n) – n наблюдений (выборка) величин X и Y. В данном пособии были использованы следующие обозначения:
. Отметим (см., например, [5]), что
Для выборочных дисперсий и ковариации справедливы следующие формулы, которые являются выборочными аналогами формул для дисперсии и ковариации: где обозначено:
Формулы (П-2) обычно используются для вычисления  и  .
Подставляя выражение
Формула для выборочного коэффициента автокорреляции временного ряда:
где t – момент времени, для которого вычисляется коэффициент автокорреляции, τ – временной лаг, n – число наблюдений ряда, yj – уровень ряда в момент времени j.
|
– выборочное среднее величины X (Y);
– выборочная дисперсия X (Y);
– выборочное среднее квадратичное отклонение X (Y);
– выборочная ковариация X и Y;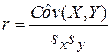
– выборочный коэффициент корреляции. (П-1)
(
) являются несмещенными оценками математического ожидания X (Y), а 
) являются смещенными оценками дисперсии.
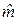коэффициента парной линейной регрессии, в соотношение (П-1) получим выражение для выборочного коэффициента корреляции, которое использовалось в §1.3 практической работы №1:
