Нормальное распределение. Вероятность отклонения от математического ожидания нормально распределенной случайной величины
№1. Нормально распределенная случайная величина X задана плотностью № 2. Случайная величина X распределена нормально с математическим ожиданием а=10. Вероятность попадания X в интервал (10, 20) равна 0, 3. Чему равна вероятность попадания X в интервал (0, 10)? № 3. Детали, выпускаемые цехом, по размеру диаметра распределяются по нормальному закону с параметрами: математическое ожидание равно 5см, а дисперсия равна 0, 81. Найти вероятность того, что диаметр наудачу взятой детали от 4 до 7см. № 4. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины X соответственно равны 10 и 2. Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале (12, 14). № 5. Производится измерение диаметра вала без систематических (одного знака) ошибок. Случайные ошибки измерения X подчинены нормальному закону со средним квадратическим отклонением σ =10мм. Найти вероятность того, что измерение будет произведено с ошибкой, не превосходящей по абсолютной величине 15мм. № 6. Распределение веса консервных банок, выпускаемых заводом, подчиняется закону нормального распределения со средним весом 250г и средним квадратическим отклонением равным 5г. Определить вероятность того, что отклонение веса банок от среднего веса по абсолютной величине не превысит 8г. № 7. Детали, выпускаемые цехом, по размеру диаметра распределяются по нормальному закону с параметрами: математическое ожидание равно 5см, а дисперсия равна 0, 81. Найти вероятность того, что диаметр наудачу взятой детали отличается от математического ожидания не более чем на 2см. № 8. На станке изготовляется шпонка, длина которой является случайной величиной, распределенной нормально: а =9; s =0, 1. Найти вероятность того, что длина шпонки будет изменяться в интервале (8, 85; 9, 15), т. е. отклонение длины от математического ожидания по абсолютной величине не превосходит 0, 15 № 9. На брус действует некоторая сила F, в результате чего брус изгибается. Прогиб в точке приложения силы является нормальной случайной величиной с а = 18мм и σ = 0, 2. Найти вероятность того, что отклонение величины прогиба от среднего по абсолютной величине не превзойдет 0, 3мм. № 10. Деталь, изготовленная автоматом, считается годной, если отклонение ее контролируемого размера от проектного не превышает 10мм. Случайные отклонения контролируемого размера от проектного подчинены нормальному закону со средним квадратическим отклонением σ =5 мм и математическим ожиданием а =0. Сколько % годных деталей изготовляет автомат? № 11. Рост взрослых женщин является случайной величиной, распределенной по нормальному закону. Математическое ожидание ее равно 164см, а среднее квадратическое отклонение 5, 5см. Найти плотность вероятности и интегральную функцию распределения этой величины. Вычислить вероятность того, что ни одна из пяти наудачу выбранных женщин не будет иметь рост более 160 см. № 12. Часовой расход топлива в двигателе скрепера представляет собой случайную величину, распределенную по нормальному закону: а =40л, σ =0, 3л. Найти вероятность того, что отклонение расхода топлива от среднего значения по абсолютной величине заключено в интервале (0, 5; 0, 7). № 13. Объемный вес строительного глиняного кирпича в среднем составляет 1800кг/см3 и представляет собой величину, распределенную нормально: σ =100кг/м3. Найти вероятность того, что отклонение объемного веса кирпича от среднего значения по абсолютной величине не превосходит 90кг/м3 и не менее 80кг/м3.
|

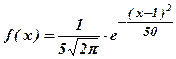 . Найти математическое ожидание и дисперсию X.
. Найти математическое ожидание и дисперсию X.


