ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ. Пример 1. По длинному прямому тонкому проводу течет ток силой
Пример 1. По длинному прямому тонкому проводу течет ток силой Решение. Магнитное поле, создаваемое прямым бесконечно длинным проводником настолько малого сечения, что абсолютная величина магнитной индукции
В формулу (1) подставим числовые значения величин и произведем вычисления:
Пример 2. Два параллельных бесконечно длинных провода D и C, по которым текут в одном направлении электрические токи силой I = 60 А, расположены на расстоянии d = 10 см друг от друга. Определить магнитную индукцию
Рис. 3. Решение: Для нахождения магнитной индукции
Абсолютное значение магнитной индукции может быть найдено по теореме косинусов:
где a – угол между векторами
Подставляя выражения
Вычислим
где d – расстояние между проводами. Отсюда:
После подстановки числовых значений получим:
Подставляя в формулу (2) значения входящих величин, определяем искомую индукцию:
Пример 3. По проводу, согнутому в виде квадрата со стороной a = 10 см, течет ток силой I = 100 А. Найти магнитную индукцию Решение. Расположим квадратный виток в плоскости чертежа (Рис. 4) согласно принципу суперпозиции магнитных полей, магнитная индукция
Магнитная индукция поля, создаваемого отрезком прямолинейного провода с током
Учитывая, что
Подставив это выражение
Заметив, что
Подставим в эту формулу числовые значения физических величин и произведем вычисления:
Пример 4. Плоский квадратный контур со стороной a = 10 см, по которому течёт ток силой I = 100 А, свободно установился в однородном магнитном поле ( 1) a1 = 90°, 2) a2 = 3°. При повороте контура сила тока в нём поддерживается неизменной. Решение: Как известно, на контур с током в магнитном поле действует момент сил (Рис. 5):
По условию задачи в начальном положении контур свободно установился в магнитном поле. При этом момент сил равен нулю (M = 0), а значит φ = 0, т. е. векторы
Работа при повороте на угол
Выразим числовые значения величин в единицах СИ: I = 100 А, B = 1 Тл, a = 10 см = 0, 1 м и подставим в (2):
Работа при повороте на угол j2 = 3°: В этом случае, учитывая, что угол j2 мал, заменим в выражении (2)
Выразим угол j2 в радианах. После подстановки числовых значений величин в (3), найдем:
Задачу можно решить и другим способом. Работа внешних сил по перемещению контура с током в магнитном поле, равна произведению силы тока в контуре на изменение магнитного потока через контур:
где
Если j 1 = 90°, то Пример 5. Электрон, пройдя ускоряющую разность потенциалов равную 400 В, попал в однородное магнитное поле напряжённостью Решение. Радиус кривизны траектории электрона определим, исходя из следующих соображений: на движущийся в магнитном поле электрон действует сила Лоренца
где
где e - заряд электрона; v – скорость электрона; R – радиус кривизны траектории; a – угол между направлением вектора скорости Из формулы (1) найдём
Входящий в равенство (2) импульс может быть выражен через кинетическую энергию T электрона:
Но кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов U, определяется равенством:
Подставив это выражение T в формулу (3), получим
Магнитная индукция B может быть выражена через напряжённость H магнитного поля в вакууме:
где Подставив найденные выражения B и mv в формулу (2), определим
Выразим все величины, входящие в формулу (4), в единицах СИ:
Подставим эти значения в формулу (4) и произведём вычисления:
Для определения частоты обращения n воспользуемся формулой, связывающей частоту со скоростью и радиусом:
Подставив в формулу (5) выражение (2) для радиуса кривизны, получим:
Все величины, входящие в эту формулу, ранее были выражены в единицах СИ. Подставим их и проведём вычисления:
Решение. Мгновенное значение ЭДС индукции
где ψ – потокосцепление. Потокосцепление связано с магнитным потоком Ф и числом N витков, плотно прилегающих друг к другу, соотношением:
Подставляя выражение Ψ в формулу (1), получим:
При вращении рамки (Рис. 6) магнитный поток, пронизывающий рамку в момент времени t, определяется соотношением:
где B – магнитная индукция, S – площадь рамки; ω – круговая (или циклическая) частота. Подставив в формулу (2) выражение Ф и, продифференцировав по времени, найдём мгновенное значение ЭДС индукции:
Круговая частота ω связана с частотой вращения n соотношением
Подставляя значения величин в формулу (3), получим:
Выразив значение величин, входящих в эту формулу, в единицах СИ:
и, подставив их в формулу (4), произведём вычисления:
Пример 7. Соленоид с сердечником из магнитного материала содержит N = 1200 витков провода, прилегающих друг к другу. При силе тока I = 4 А магнитный поток Ф = 6 мкВб. Определить индуктивность L соленоида и энергию W магнитного поля соленоида. Решение: Индуктивность L связана с потокосцеплением Ψ и силой тока I соотношением:
Потокосцепление в свою очередь может быть выражено через поток и число витков N (при условии, что витки плотно прилегают друг к другу):
Из выражений (1) и (2) находим интересующую нас индуктивность соленоида:
Выразим все величины в единицах СИ: N = 1200, Ф = 6 10-6 Вб, I = 4 А. Подставим их значения в формулу (3) и произведём вычисления:
Энергия W магнитного поля соленоида с индуктивностью L при силе тока I, протекающего по его обмотке, может быть вычислена по формуле:
Подставив в эту формулу полученное ранее выражение индуктивности (3) и, произведя вычисления, получим:
|

 . Определить магнитную индукцию
. Определить магнитную индукцию  поля, создаваемого проводником в точке, удаленной от него на расстояние r = 4 см.
поля, создаваемого проводником в точке, удаленной от него на расстояние r = 4 см. в данной точке будет зависеть только от её расстояния до проводника. Поэтому все точки на окружности радиуса
в данной точке будет зависеть только от её расстояния до проводника. Поэтому все точки на окружности радиуса  (рис. 2), лежащей в плоскости, перпендикулярной проводнику, будут иметь одинаковое значение магнитной индукции:
(рис. 2), лежащей в плоскости, перпендикулярной проводнику, будут иметь одинаковое значение магнитной индукции: ,
, где
где  - магнитная постоянная.
- магнитная постоянная. Направление вектора
Направление вектора  .
.

 и
и  полей, создаваемых каждым проводником с током в отдельности, и сложим их геометрически:
полей, создаваемых каждым проводником с током в отдельности, и сложим их геометрически: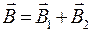 .
. . (1)
. (1) 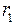 и
и  от проводников до точки A:
от проводников до точки A: ;
;  .
. и
и 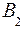 в формулу (2) и вынося
в формулу (2) и вынося 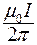 за знак корня, получим:
за знак корня, получим: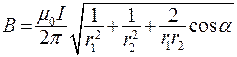 . (2)
. (2) . Заметим, что
. Заметим, что  (как углы с соответственно перпендикулярными сторонами), по теореме косинусов запишем:
(как углы с соответственно перпендикулярными сторонами), по теореме косинусов запишем: ,
, .
.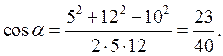
 .
. . (1)
. (1)
 В точке O пересечения диагоналей квадрата все векторы индукции будут направлены перпендикулярно плоскости витка «к нам». Кроме того, из соображений симметрии следует, что абсолютные значения этих векторов одинаковы:
В точке O пересечения диагоналей квадрата все векторы индукции будут направлены перпендикулярно плоскости витка «к нам». Кроме того, из соображений симметрии следует, что абсолютные значения этих векторов одинаковы:  . Это позволяет векторное равенство (1) заменить скалярным равенством:
. Это позволяет векторное равенство (1) заменить скалярным равенством: . (2)
. (2) . (3)
. (3) и
и  , формулу (3) можно переписать в виде:
, формулу (3) можно переписать в виде: .
. .
. и
и 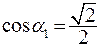 (т.к.
(т.к. 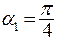 ), получим:
), получим: .
. .
. ). Определить работу A, совершаемую внешними силами при повороте контура относительно оси, проходящей через середину его противоположных сторон, на угол:
). Определить работу A, совершаемую внешними силами при повороте контура относительно оси, проходящей через середину его противоположных сторон, на угол: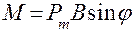 , (1)
, (1)
 где
где 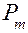 - магнитный момент контура; B – магнитная индукция; φ – угол между вектором
- магнитный момент контура; B – магнитная индукция; φ – угол между вектором 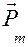 , направленным по нормали к контуру, и вектором
, направленным по нормали к контуру, и вектором  и
и  ; Подставив сюда выражение M по формуле (1) и учтя, что
; Подставив сюда выражение M по формуле (1) и учтя, что  , где I – сила тока в контуре;
, где I – сила тока в контуре;  - площадь контура, получим
- площадь контура, получим 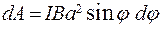 . Взяв интеграл от этого выражения, найдём работу при повороте на конечный угол:
. Взяв интеграл от этого выражения, найдём работу при повороте на конечный угол: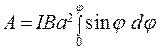 .
. :
: . (2)
. (2) .
. :
: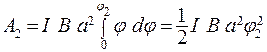 (3)
(3)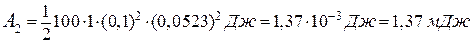 .
. ,
, – магнитный поток, пронизывающий контур до перемещения.
– магнитный поток, пронизывающий контур до перемещения. – магнитный поток, пронизывающий контур после перемещения.
– магнитный поток, пронизывающий контур после перемещения.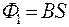 ,
,  . Следовательно,
. Следовательно,  , что совпадает с полученным выше результатом (3).
, что совпадает с полученным выше результатом (3). . Определить радиус R кривизны траектории и частоту n обращения электрона в магнитном поле. Вектор скорости перпендикулярен линиям поля.
. Определить радиус R кривизны траектории и частоту n обращения электрона в магнитном поле. Вектор скорости перпендикулярен линиям поля. (действием силы тяжести можно пренебречь). Сила Лоренца перпендикулярна вектору скорости и, следовательно, сообщает электрону нормальное ускорение. По второму закону Ньютона можно записать
(действием силы тяжести можно пренебречь). Сила Лоренца перпендикулярна вектору скорости и, следовательно, сообщает электрону нормальное ускорение. По второму закону Ньютона можно записать ,
, - нормальное ускорение или
- нормальное ускорение или , (1)
, (1)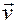 и вектором
и вектором  и a = 90°,
и a = 90°,  ).
).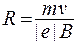 . (2)
. (2) . (3)
. (3) .
. .
. .
. . (4)
. (4) (из справочной табл.),
(из справочной табл.), ,
, ,
,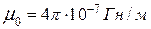 ,
, .
.
 . (5)
. (5)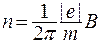 , или
, или 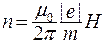 .
. .
.
 Пример 6. В однородном магнитном поле (B = 0, 1 Тл) равномерно с частотой
Пример 6. В однородном магнитном поле (B = 0, 1 Тл) равномерно с частотой 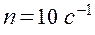 вращается рамка, содержащая N = 1000 витков, плотно прилегающих друг к другу. Площадь рамки S = 150 см2. Определить мгновенное значение ЭДС индукции
вращается рамка, содержащая N = 1000 витков, плотно прилегающих друг к другу. Площадь рамки S = 150 см2. Определить мгновенное значение ЭДС индукции  , соответствующее углу поворота рамки в 30°.
, соответствующее углу поворота рамки в 30°.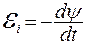 , (1)
, (1) .
.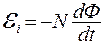 . (2)
. (2) ,
, . (3)
. (3) .
. . (4)
. (4)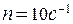 ,
, 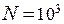 ,
,  ,
,  ,
,  ,
,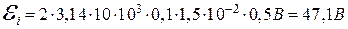 .
. . (1)
. (1) . (2)
. (2)  . (3)
. (3) .
. .
.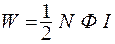 .
. .
.


