ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ. Пример 1. В вершинах квадрата расположены равные положительные заряды (рис.1)
Пример 1. В вершинах квадрата расположены равные положительные заряды Дано: Найти:
Рис. 1 Решение: Для определения величины q 5 используем закон Кулона. Заряды q1, q2, q3, q4 одинаковы и расположены симметрично. Определим условия, при которых один из зарядов, например
где
Переходим от векторного к скалярному выражению, здесь
Определяем величину заряда, применяя закон Кулона: Так как
Кроме того, по условию
Подставляя в (4) . Производим вычисления в единицах СИ:
Пример 2. Два одинаковых положительных заряда 10-7 Кл находятся в воздухе на расстоянии 8 см друг от друга. Определить напряженность в точке О, находящейся на середине отрезка, соединяющего заряды, и в точке А, расположенной на расстоянии 5 см от зарядов. Дано: Решение: Напряженность поля, создаваемого зарядами, находится по принципу суперпозиции. Результирующая напряженность Е определяется векторной суммой напряженностей, создаваемых каждым зарядом в данной точке поля:
где
Чтобы найти числовые значения напряженности в точке О, надо сначала построить векторы напряженностей
Рис. 2 Кроме того, заряды равны и расположены на равном расстоянии от точки О. Поэтому с учетом направления векторов из формулы (1) следует:
В точке А напряженность вычисляется по формуле (1) при аналогичном построении векторов. Результирующий вектор напряженности
Проверяем единицу измерения: Пример 3. Установить, как изменится емкость и энергия плоского воздушного конденсатора, если параллельно его обкладкам ввести металлическую пластину толщиной 1 мм. Площадь обкладки конденсатора и пластины 150 см2, расстояние между обкладками 6 мм. Конденсатор заряжен до 400 В и отключен от батареи. Дано: Найти: Решение: Емкость и энергия конденсатора при внесении в него металлической пластины будут изменяться. Это вызвано тем, что уменьшается расстояние между пластинами от d до d-d0 (рис.3). Используем формулу электроемкости плоского конденсатора.
где S - площадь пластины, d - расстояние между пластинами.
Рис.3. В нашем случае
Проводим вычисления в системе СИ:
Проверим единицу измерения СИ:
Так как электрическое поле в плоском конденсаторе однородно, плотность энергии во всех его точках одинакова и равна
Следовательно, изменение энергии (конечное значение меньше начального) произошло вследствие уменьшения объема поля конденсатора:
Напряженность поля Е определяется через градиент потенциала
где U - разность потенциалов, d - расстояние между обкладками. Расчетная формула (3) с учетом формулы (4) примет вид:
Подставляя числовые значения (в единицах СИ) в формулу (5), получаем:
Проверяем единицу измерения:
Пример 4. Плоский воздушный конденсатор из двух пластин, расположенных на расстоянии 4 мм друг от друга, общей площадью 100 см2. Конденсатор заряжают от батареи в 200 В и отключают от нее. Какую работу нужно совершить, чтобы увеличить расстояние между обкладками в два раза? Решить задачу при условии, когда конденсатор не отключают от батареи. Дано: Найти: А. Решение: Чтобы увеличить расстояние между обкладками конденсатора, отключенного от батареи, необходимо совершить работу под действием внешних сил. Работа внешних сил
Приложенная сила определяется силой взаимодействия между пластинами
где q - заряд пластины, E1 - напряженность поля одной пластины. Величина напряженности может быть получена через градиент потенциала
Заряд пластины, перемещаемый относительно другой пластины, может быть найден по площади пластины S, расстоянию между обеими пластинами l и разности потенциалов U. Из формулы емкости плоского конденсатора
Проведя подстановку формул (2-4) в уравнение (1), получаем
Для определения полной работы необходимо учесть, что при отключенном конденсаторе напряжение изменяется, но заряд q и напряженность поля Е остаются неизменными:
Подставим выражение (6) в уравнение (5) и проинтегрируем:
Подставляя в (7) числовые значения (в единицах СИ, находим)
Пример 5. Найти токи, протекающие в каждой ветви электрической цепи (рис. 4), если Дано: Найти
Рис.4. Решение: Задача дана для расчета разветвленных цепей, когда в них есть несколько источников тока. При решении задач такого типа рационально пользоваться законами (правилами) Кирхгофа. Первый закон сформулирован для узлов, т.е. точек разветвления цепи, в которых сходится больше двух проводников: алгебраическая сумма токов, сходящихся в узле равна нулю Второй закон для замкнутых контуров гласит: в любом замкнутом контуре алгебраическая сумма произведений сил токов на сопротивления соответствующих участков этого контура равна алгебраической сумме ЭДС в контуре Решая совместно составленные по этим правилам уравнения, можно определить ту или иную искомую величину (сопротивления внешней цепи или силы токов, ЭДС). Для составления уравнений по указанным законам надо придерживаться следующих правил: 1. Обозначить на схеме буквами узлы и контуры. 2. Произвольно выбрать направление токов (если они не оговорены условием задачи) во всех участках цепи и обозначить их на чертеже стрелками. 3. Учесть направление токов при составлении уравнения по первому закону. Положительными считать токи, подходящие к узлу, отрицательными - отходящие от узла. 4. Составить систему уравнений для первого закона Кирхгофа. Число уравнений, составленных по этому правилу, должно быть на единицу меньше числа узлов в цепи. 5. Выбрать произвольно направление обхода контура. Условиться, что ЭДС в уравнении будет положительна, если направление от положительного полюса к отрицательному вне источника тока совпадает с направлением обхода, в противном случае ЭДС отрицательна. 6. Считать падение напряжения в цепи положительным, если выбранное ранее направление тока на этом участке (между двумя узлами) совпадает с направлением обхода контура, и отрицательным, если направление тока не совпадает с направлением обхода контура. 7. Первый контур выбирается произвольно. При составлении уравнений для следующих контуров надо включать в них контуры, ранее не входившие. 8. Число уравнений, составленных по второму закону Кирхгофа, определяется следующим условием. Если число контуров в цепи m, а узлов в ней n, то число независимых уравнений, достаточных для решения, равно m - n+1. 9. Получение в ответе токов с отрицательными знаками означает только то, что было выбрано направление, обратное действительному. Согласно сформулированным выше правилам, решаем задачу 5: 1) Обозначим на схеме контуры, узлы, направления токов. 2) Устанавливаем m - число ветвей (в данной схеме их 3) и n - число узлов (в данной схеме их 2 - в точках В и Н, (см. рис.4). 3) Для составления уравнения по первому закону Кирхгофа следует выбрать один из указанных узлов. Выбираем узел В, в котором сходятся токи трех проводников. Учитывая направление токов, получим
4) Устанавливаем число уравнений, необходимых для решения задач по второму закону Кирхгофа. Это число уравнений равно m - n+1 = 3 – 2 + 1 = 2. Выбираем контуры ВСДНВ и АВНТА. Устанавливаем обход по контуру ВСДНВ. Учитывая правило знаков, выбираем обход по часовой стрелке, при котором ЭДС
Составляем уравнение для второго контура. Для этого устанавливаем направление обхода для контура А В Н Т А. Так как в этом контуре два источника тока и
Из уравнения (1) находим
Для определения числовых результатов подставляем в формулу (2) и (3) известные числовые значения сопротивления и ЭДС.
После сложения (5) и (6) получим
Подставляя полученную силу тока
Следовательно
Силу тока
Зная I3 из формулы (7), находим
Определяем значение I2 из выражения (4)
Задача 6. Найти сопротивление железного стержня диаметром 1 мм, если масса этого стержня 1 кг. Решение. Сопротивление стержня можно рассчитать по формуле где R - сопротивление, Площадь сечения круглого стержня определяется
Из справочных таблиц находим
тогда
|

 (рис.1). В центр квадрата помещен отрицательный заряд. Вычислить, какой величины должен быть этот заряд, чтобы уравновесить силу взаимного отталкивания зарядов, расположенных по вершинам квадрата.
(рис.1). В центр квадрата помещен отрицательный заряд. Вычислить, какой величины должен быть этот заряд, чтобы уравновесить силу взаимного отталкивания зарядов, расположенных по вершинам квадрата. Кл.
Кл.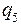
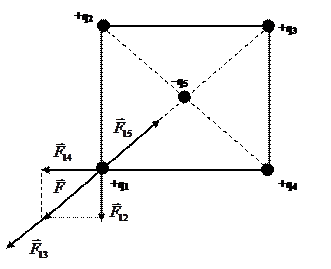

 , находился бы в равновесии с зарядом
, находился бы в равновесии с зарядом  ,
,  ,
, 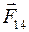 . Чтобы выполнить условие равновесия зарядов
. Чтобы выполнить условие равновесия зарядов  , (1)
, (1)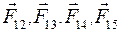 - силы, действующие со стороны зарядов q2, q3, q4. и
- силы, действующие со стороны зарядов q2, q3, q4. и  на
на  и получим:
и получим: . (2)
. (2)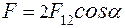
 . (3)
. (3) .
. , то
, то . (4)
. (4) , тогда
, тогда . (5)
. (5) и
и  из (5), после преобразования получим:
из (5), после преобразования получим: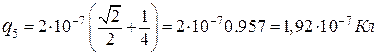 .
.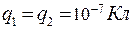 ,
, 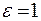 , 2 r= 8 см = 0, 08 м, r1 = 0, 05 м. Найти Е0 и Е.
, 2 r= 8 см = 0, 08 м, r1 = 0, 05 м. Найти Е0 и Е.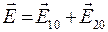 , (1)
, (1) и
и  - величины напряженностей полей, определяемых по формуле
- величины напряженностей полей, определяемых по формуле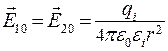 . (2)
. (2)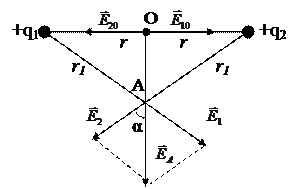

 ,
,  , отсюда получаем
, отсюда получаем  .
. является диагональю параллелограмма (см. рис.2), следовательно,
является диагональю параллелограмма (см. рис.2), следовательно,  или
или  , т.к.
, т.к.  .Численное значение напряженности поля в точке А определяется по формуле
.Численное значение напряженности поля в точке А определяется по формуле ,
,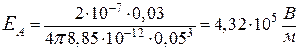 , h = OA = 0, 03 м.
, h = OA = 0, 03 м. .
. = 1,
= 1,  = 1 мм = 10-3 м, S = 150 см2 =
= 1 мм = 10-3 м, S = 150 см2 =  , d = 6 мм =
, d = 6 мм =  , U = 400 В.
, U = 400 В.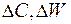 .
. , (1)
, (1)

 . (2)
. (2) .
. .
. , где Е - напряженность поля между обкладками. При внесении металлической пластины параллельно обкладкам напряженность поля остается неизменной, а объем электрического поля уменьшился на
, где Е - напряженность поля между обкладками. При внесении металлической пластины параллельно обкладкам напряженность поля остается неизменной, а объем электрического поля уменьшился на .
. . (3)
. (3) , (4)
, (4) . (5)
. (5) .
. .
. = 4 мм =
= 4 мм =  , S1= S2 = 50 см2 =
, S1= S2 = 50 см2 =  ,
,  = 8 мм =
= 8 мм =  , U0 = 200 В.
, U0 = 200 В. зависит от приложенной силы F и перемещения от
зависит от приложенной силы F и перемещения от  . (1)
. (1) , (2)
, (2) . (3)
. (3) ,
,  получаем
получаем . (4)
. (4) . (5)
. (5) . (6)
. (6) . (7)
. (7) .
. = 130 В,
= 130 В,  = 117 В, R
= 117 В, R  = 0, 5 Ом, R
= 0, 5 Ом, R  = 0, 3 Ом, R
= 0, 3 Ом, R  = 12 Ом. Внутреннее сопротивление источников ЭДС не учитывать.
= 12 Ом. Внутреннее сопротивление источников ЭДС не учитывать. = 117 В, R
= 117 В, R 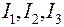


 .
. .
. . (1)
. (1) . (2)
. (2)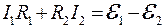 . (3)
. (3) . (4)
. (4) , (5)
, (5) . (6)
. (6) . (7)
. (7) 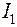 в (4), находим
в (4), находим .
. . (8 )
. (8 ) (8) используем в выражении (5):
(8) используем в выражении (5): ,
, . (9)
. (9) . (10)
. (10) .
. ,
, - удельное сопротивление. l - длина стержня, S – площадь поперечного сечения стержня.
- удельное сопротивление. l - длина стержня, S – площадь поперечного сечения стержня. , где d - диаметр стержня. Длина стержня выразится из его массы:
, где d - диаметр стержня. Длина стержня выразится из его массы: 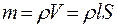 , где m - масса стержня,
, где m - масса стержня,  - удельная плотность материала стержня, V - объем стержня,
- удельная плотность материала стержня, V - объем стержня, 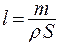 . Подставив найденные значения S и l в формулу для R. получим:
. Подставив найденные значения S и l в формулу для R. получим: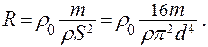
 ,
, .
.


