ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ. Пример 1. Определить число N молекул, содержащихся в объеме V = 1 мм3 воды, массу молекулы воды
Пример 1. Определить число N молекул, содержащихся в объеме V = 1 мм3 воды, массу Решение: Число N молекул, содержащихся в некоторой массе равно произведению числа Авогадро
так как количество вещества:
μ - молярная масса, то
Выразив в этой формуле массу, как произведение плотности
Подставим в формулу (1) следующие значения величин: V = 1 мм3 =
Массу Подставим сюда числовые значения μ и
Если молекулы воды плотно прилегают друг к другу, то можно считать, что на каждую молекулу приходится объем (кубическая ячейка)
Объем
Подставим полученное выражение Входящий в эту формулу молярный объем определяется выражением
Проверим, дает ли правая часть выражения (3) единицу длины:
Теперь подставим числовые значения физических величин в формулу (3) и произведем вычисления:
Пример 2. В баллоне объемом V = 10 л находится гелий под давлением Р Решение: Для решения задачи воспользуемся уравнением Менделеева-Клапейрона, применив его к конечному состоянию газа:
где
Массу гелия m2 выразим через массу m1, соответствующую начальному состоянию и массу m гелия, взятого из баллона:
Массу гелия m найдем также из уравнения Менделеева-Клапейрона, применив его к начальному состоянию
Подставляя в выражение (3) массу из формулы (4), а затем полученное выражение в формулу (2), найдем:
После преобразования и сокращения находим:
Левая часть расчётной формулы (5) выражает давление, имеет размерность
что совпадает с размерностью давления. Убедившись в том, что размерность правой и левой частей формулы (5) одинаковы, выразим величины, входящие в эту формулу, в единицах СИ и произведем вычисления: P1 = 1 МПа =106 Па, R = 8, 31 Дж/(мольК), T1 = 300 К, T2 = 290 К, V = 10 л = 10-2 м3 ,
Пример 3. Баллон содержит Решение. По закону Дальтона давление смеси равно сумме парциальных давлений газов, входящих всостав смеси. Парциальным давлением газа называется давление, которое производил бы этот газ, если бы только он один находился в сосуде, занятым смесью. По уравнению Менделеева-Клапейрона, парциальные давления кислорода
Следовательно, по закону Дальтона давление смеси газов
откуда объем баллона:
Выразим в единицах СИ числовые значения величин, входящих в эту формулу m1 = 80 г = 0, 8 кг,
Пример 4. Найти среднюю кинетическую энергию Решение: Известно, что на каждую степень свободы молекулы газа приходится одинаковая средняя энергия
Подставив в формулу (1) значение
Число всех молекул газа можно вычислить по формуле:
где
Подставив это выражение в формулу (2) получим:
Выразим величины, входящие в эту формулу, в единицах СИ:
Пример 5. Вычислить удельные теплоемкости при постоянном объеме Решение: Удельные теплоемкости идеальных газов выражаются формулами
где Для водорода (двухатомный газ)
Пример 6. Вычислить удельные теплоемкости Решение: Удельную теплоемкость смеси при постоянном объеме
где
отсюда
или
где
Рассуждая таким же образом, получим формулу для вычисления удельной теплоемкости смеси при постоянном давлении:
Подставим в формулу (5) числовые значения величин:
Пример 7. Кислород массой m = 2 к г занимает объем равный V = 1 м3 и находится под давлением P Решение: Изменение внутренней энергии газа выражается формулой:
где i - число степеней свободы молекул газа (для двухатомных молекул кислорода i = 5), μ - молярная масса. Начальную и конечную температуру газа найдем из уравнения Клапейрона-Менделеева:
Выпишем заданные величины в единицах системы СИ:
Подставляя в выражение (1) числовые значения величин, входящих в него и выполняя арифметические действия, находим:
Работа расширения газа при постоянном давлении выражается формулой:
Подставим числовые значения величин, получим:
Работа газа, нагреваемого при постоянном объеме, равна нулю, т.е.
Согласнопервому началу термодинамики теплота Q, переданная газу, равна сумме изменения внутренней энергии и работы A: Пример 8. Тепловая машина работает по обратному циклу Карно. Температура нагревателя T Решение: Термический КПД тепловой машины, называемый также коэффициентом использованной теплоты, показывает, какая доля теплоты, полученной от нагревателя, превращается в механическую работу. Термический КПД выражается формулой:
где Q
Зная КПД цикла, можно по формуле
Подставив в эту формулу полученное значение КПД и температуры T
Пример 9. Найти добавочное давление внутри мыльного пузыря диаметром d = 10 см. Какую работу нужно совершить, чтобы выдуть этот пузырь? Решение: Пленка мыльного пузыря имеет две сферические поверхности - внешнюю и внутреннюю. Обе поверхности оказывают давление на воздух, заключенный внутри пузыря. Так как толщина пленки чрезвычайно мала, то диаметры обеих поверхностей практически одинаковы. Поэтому добавочное давление, где
Работа, которую нужно совершить, чтобы, растягивая пленку, увеличить её поверхность на
В данном случае
Подставив числовые значения величин, получим:
|

 молекулы воды. Считая условно, что молекулы воды имеют вид шариков, соприкасающихся друг с другом, найти диаметр d молекул.
молекулы воды. Считая условно, что молекулы воды имеют вид шариков, соприкасающихся друг с другом, найти диаметр d молекул.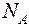 на количество вещества
на количество вещества  :
:


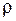 на объем V, получим
на объем V, получим . (1)
. (1) = 103 кг/м3,
= 103 кг/м3, м
м  , μ =
, μ =  кг/моль,
кг/моль,  моль
моль  и произведем вычисления:
и произведем вычисления: молекул = 3, 34 1019молекул.
молекул = 3, 34 1019молекул. , одной молекулы можно найти делением молярной массы на число Авогадро:
, одной молекулы можно найти делением молярной массы на число Авогадро: 
 кг =
кг =  кг.
кг. , где d - диаметр молекулы воды. Отсюда
, где d - диаметр молекулы воды. Отсюда (2)
(2)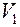 найдем, разделив молярный объем
найдем, разделив молярный объем  на число молекул в моле, т.е. на число Авогадро
на число молекул в моле, т.е. на число Авогадро 
 , тогда искомый диаметр молекулы:
, тогда искомый диаметр молекулы: (3)
(3)

 = 1 МПа и при температуре Т
= 1 МПа и при температуре Т  = 290 К. Определить давление Р
= 290 К. Определить давление Р  (1)
(1) - масса гелия в баллоне в конечном состоянии, μ - молярная масса гелия, R - универсальная газовая постоянная. Из уравнения (1) выразим искомое давление Р
- масса гелия в баллоне в конечном состоянии, μ - молярная масса гелия, R - универсальная газовая постоянная. Из уравнения (1) выразим искомое давление Р 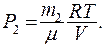 (2)
(2) (3)
(3) (4)
(4)
 (5)
(5) . Проверим размерность правой части. Размерность первого слагаемого не вызывает сомнения, т.к. отношение температур – величина безразмерная. Размерность второго слагаемого:
. Проверим размерность правой части. Размерность первого слагаемого не вызывает сомнения, т.к. отношение температур – величина безразмерная. Размерность второго слагаемого:
 ,
,  ,
,
 и аргона
и аргона 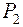 выражается формулами:
выражается формулами:


 , m2 = 330 г = 0, 33 кг,
, m2 = 330 г = 0, 33 кг,  , m2 = 40 10-3 кг/моль, P1 = 1 МПа = 106 Па, R = 8, 31 Дж/(мольК), подставим числовые значения в формулу и произведем вычисления:
, m2 = 40 10-3 кг/моль, P1 = 1 МПа = 106 Па, R = 8, 31 Дж/(мольК), подставим числовые значения в формулу и произведем вычисления:
 вращательного движения одной молекулы кислорода при температуре Т = 350 К, а также кинетическую энергию
вращательного движения одной молекулы кислорода при температуре Т = 350 К, а также кинетическую энергию 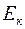 вращательного движения всех молекул кислорода массой m = 4 г.
вращательного движения всех молекул кислорода массой m = 4 г. , где
, где 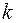 - постоянная Больцмана, Т - абсолютная температура газа. Так как вращательному движению двухатомной молекулы (молекула кислорода двухатомная) соответствует две степени свободы, то средняя энергия вращательного движения молекулы кислорода выразится формулой:
- постоянная Больцмана, Т - абсолютная температура газа. Так как вращательному движению двухатомной молекулы (молекула кислорода двухатомная) соответствует две степени свободы, то средняя энергия вращательного движения молекулы кислорода выразится формулой: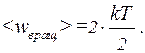 (1)
(1) и T = 350 К получим
и T = 350 К получим  . Кинетическая энергия вращательного движения всех молекул газа определяется равенством:
. Кинетическая энергия вращательного движения всех молекул газа определяется равенством: (2)
(2) (3)
(3) число Авогадро,
число Авогадро,  - количество вещества. Если учесть, что количество вещества
- количество вещества. Если учесть, что количество вещества  , где
, где 
 (4)
(4) ,
,  ,
, 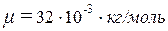 ,
,  . Подставив эти значения в формулу (4), найдем:
. Подставив эти значения в формулу (4), найдем: 
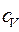 и при постоянном давлении
и при постоянном давлении 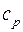 неона и водорода, принимая эти газы за идеальные.
неона и водорода, принимая эти газы за идеальные.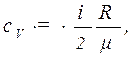 (1)
(1) (2)
(2) - число степеней свободы молекул газа,
- число степеней свободы молекул газа,  - молярная масса. Для неона (одноатомный газ)
- молярная масса. Для неона (одноатомный газ)  ,
,  кг/моль (см. справочную таблицу). Вычисляя по формулам (1) и (2), получим:
кг/моль (см. справочную таблицу). Вычисляя по формулам (1) и (2), получим: 

 ,
,  кг/моль. Вычисляя по тем же формулам, получим:
кг/моль. Вычисляя по тем же формулам, получим:

 и
и  = 80%, массовая доля водорода
= 80%, массовая доля водорода  = 20%. Значение удельных теплоемкостей газов взять из предыдущего примера.
= 20%. Значение удельных теплоемкостей газов взять из предыдущего примера.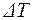 , выразим двумя способами.
, выразим двумя способами.
 (1)
(1) (2)
(2) - удельная теплоемкость неона,
- удельная теплоемкость неона,  - удельная теплоемкость водорода. Приравняв правые части (1) и (2) и разделив обе части полученного равенства на
- удельная теплоемкость водорода. Приравняв правые части (1) и (2) и разделив обе части полученного равенства на 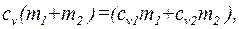
 (3)
(3) (4)
(4) и
и  - массовые доли неона и водорода в смеси. Подставив в формулу (4) числовые значения величин, найдем:
- массовые доли неона и водорода в смеси. Подставив в формулу (4) числовые значения величин, найдем:
 (5)
(5) 
 = 0, 5 МПа. Найти изменение внутренней энергии газа, совершенную им работу А и теплоту Q, переданную газу. Построить график процесса.
= 0, 5 МПа. Найти изменение внутренней энергии газа, совершенную им работу А и теплоту Q, переданную газу. Построить график процесса. (1)
(1) (2)
(2) ,
,  кг/моль,
кг/моль, 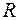 = 8, 31 Дж/моль К, V
= 8, 31 Дж/моль К, V  105 Па, Р
105 Па, Р  ;
; ;
; 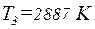 .
.

 .
. . Следовательно, полная работа, совершенная газом, равна
. Следовательно, полная работа, совершенная газом, равна =
= 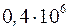 Дж.
Дж. , следовательно
, следовательно  .
.

 определить температуру охладителя Т2:
определить температуру охладителя Т2:

 -. где
-. где  радиус пузыря. Так как
радиус пузыря. Так как  , то
, то  . Коэффициент поверхностного натяжения мыльной воды 40 мН/м (см. справочную табл.) диаметр пузыря = 10 см = 0, 1 м.
. Коэффициент поверхностного натяжения мыльной воды 40 мН/м (см. справочную табл.) диаметр пузыря = 10 см = 0, 1 м.
 , выражается формулой
, выражается формулой
 - общая площадь двух сферических поверхностей пленки, затягивающей отверстие трубки до выдувания пузыря, пренебрегая
- общая площадь двух сферических поверхностей пленки, затягивающей отверстие трубки до выдувания пузыря, пренебрегая 
 .
.


