ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ. 100. Путь, пройденный точкой, выражен уравнением
100. Путь, пройденный точкой, выражен уравнением 101. Два тела свободно падают с одинаковой высоты. Промежуток времени между началом движения первого и началом движения второго тела равен 102. Скорость автомобиля при движении в гору 20 км/ч, а с горы 60 км/ч. Определить среднюю путевую скорость автомобиля, если путь, пройденный за подъем, такой же, как при спуске. 103. На какую высоту поднимется тело, брошенное вертикально вверх с начальной скоростью 200 м/с? Сопротивлением воздуха пренебречь. 104. Вертикально верх с высоты 392 м с начальной скоростью 19, 6 м/с брошено тело. Через какое время оно упадет на землю? 105. Самолет летит на высоте 4000 метров со скоростью 800 км/ч. На каком расстоянии до цели (считая по горизонтали) летчик должен сбросить бомбу, чтобы она попала в цель? Сопротивлением воздуха пренебречь. 106. Тело брошено вертикально вверх с начальной скоростью 28 м/с. На какую наибольшую высоту оно поднимется и чему равно время подъема? 107. Мяч брошен горизонтально с крыши высокого здания со скоростью 10, 6 м/с. Определить местоположение и скорость мяча через 4 с. Сопротивлением воздуха пренебречь. 108. Снаряд выпущен из орудия под углом в 40° к горизонту с начальной скоростью 600 м/с. Найти дальность полета снаряда. Сопротивлением воздуха пренебречь. 109. Под каким углом к горизонту надо бросить тело, чтобы дальность полета была в 4 раза больше, чем наибольшая высота полета. Сопротивлением воздуха пренебречь. 110. Определить сколько оборотов в секунду совершает колесо велосипеда, движущегося со скоростью 40 км/ч. Диаметр колеса 70 см. 111. Материальная точка движется по окружности с радиусом 5 метров. Угол поворота радиус-вектора этой точки связан со временем движения соотношением 112. На шкив радиусом 10 см. намотана нить, к которой привязан груз. Под действием груза шкив приходит во вращательное движение, причем за 5 с, двигаясь равноускоренно, он опускается на 2, 5 м. Определить линейную и угловую скорость точек цилиндрической поверхности шкива в конце 7 секунды и угловое ускорение шкива. 113. Автомобиль движется по закруглению радиусом 500 м с тангенциальным ускорением 0, 05 м/с2. Определить его нормальное и полное ускорение в тот момент, когда его скорость равна 5 м/с. 114. Линейная скорость некоторой точки вращающегося диска равна 2 м/с. Точка, лежащая на том же радиусе, но на 10 см дальше от центра, имеет линейную скорость 3 м/с. Определить, сколько оборотов в секунду совершает диск. 115. Определить полное ускорение 116. Найти радиус вращающегося колеса, если известно, что линейная скорость точки, лежащей на ободе, в 3 раза больше линейной скорости 117. Точка движется по окружности радиусом 118. Колесо вращается с постоянным угловым ускорениемe = 2 рад/с2 Через t = 0, 5 с после начала движения полное ускорение колеса стало равно a = 20 см/с2. Найти радиус колеса. 119. Точка движется по окружности радиусом 120. Космический корабль массой 121. C какой угловой скоростью должен вращаться вокруг оси космический корабль с рабочим помещением в виде тороида, больший радиус которого 20 м, чтобы искусственная сила тяжести по величине равнялась земной.? 122. Тело массой 2 кг движется прямолинейно, при этом зависимость пройденного пути от времени определяется законом 123. Груз массой 124. С каким ускорением должна двигаться ракета, чтобы, пройдя расстояние 200 км, развить вторую космическую скорость ( 125. Искусственный спутник Земли имеет период обращения 2 часа. Считая траекторию спутника круговой, найти, на какой высоте над поверхностью Земли движется спутник. Радиус Земли принять за 6400 км. 126. Спутник обращается вокруг Земли по круговой орбите на высоте h = 520 км. Определить период обращения спутника. Считать известным ускорение 127. Определить напряженность гравитационного поля 128. Тело массой 129. Найти зависимость ускорения свободного падения от высоты h тела над уровнем моря на полюсе Земли. На каком расстоянии от поверхности Земли ускорение уменьшится вдвое? 130. На брусок массой m = 5 кг в горизонтальном направлении действует сила F = 20 Н. Определить ускорение, с которым движется брусок, если коэффициент трения с горизонтальной поверхностью k = 0, 4. 131. Определить, с какой скоростью двигался автомобиль, если длина следа заторможенных колес оказалась равной l = 25 м. Коэффициент трения покрышек о покрытие дороги k = 0, 3. 132. Пуля, двигаясь со скоростью 133. Вагон массой 40 т, движущийся со скоростью 2 м/с, в конце пути ударяется о пружинный амортизатор. Насколько он сожмет пружину, коэффициент упругости у которой 134. Две пружины жесткостью 135. Вагон массой m = 35 т движется на упор со скоростью v = 0, 2 м/с. При полном торможении вагона буферные пружины сжимаются на 136. Камень, пущенный по поверхности льда со скоростью V = 2 м/с, прошел до полной остановки расстояние S = 20 м. Найти коэффициент трения камня по льду. 137. Тело скользит сначала по наклонной плоскости, составляющей с горизонтом угол a = 10о, а затем по горизонтальной поверхности. Найти коэффициент трения, если расстояние, пройденное по наклонной плоскости и по горизонтали равны. 138. Тело массой m = 100 кг поднимают по наклонной плоскости с ускорением 139. Тело массой m = 50 кг тянут равномерно по полу с помощью веревки, образующей угол a = 30о с полом. Коэффициент трения k = 0, 4. Определить силу, под действием которой движется тело. 140. Груз, массой 200 кг поднимается равноускоренно на высоту 4 м за 2 с. Определить совершаемую при этом работу. 141. Некоторое тело движется прямолинейно под действием силы, являющейся функцией времени F = 2t3+8t, а пройденный телом путь определяется соотношением S = 3t3+t, где все величины выражены в системе СИ. Определить работу, произведенную силой за 10 с после начала движения. 142. Пуля массой 9 г, летевшая со скоростью 600 м/с, попадает в кирпичную стену и проникает в нее на глубину 20 см. Определить среднюю силу сопротивления кирпича движению пули. 143. Тело массой 144. Шар массой 145. Два одинаковых шара подвешены на нитях l = 0, 98 м и касаются друг друга. Один из шаров отклоняется на угол a = 10о и отпускается. Определить максимальную скорость второго шара после соударения. Удар считать идеально упругим. 146. При горизонтальном полете со скоростью v = 250 м/с снаряд массой m = 8 кг разорвался на две части. Большая часть массы m1 = 6 кг получила скорость 147. Снаряд, летевший со скоростью v = 800 м/с разорвался на два осколка. Меньший осколок, масса которого составляет 40% от массы снаряда, полетел в противоположном направлении со скоростью 148. Шар массой m1 = 5 кг движется со скоростью 149. С наклонной плоскости высотой h = 3 м соскальзывает без трения тело массой m = 0, 5 кг. Определить изменение 150. Однородный стержень длинной 1 м совершает малые колебания около горизонтальной оси, проходящей через точку стержня, отстоящую на 25 см от верхнего конца стержня. Определить период колебания стержня. 151. Найти момент инерции однородного тонкого стержня массой m и длиной l относительно оси, перпендикулярной его длине и проходящей через точку стержня, отстоящую на 1/3 l от ее конца. 152. Найти кинетическую энергию и момент инерции сплошного цилиндра, который катится без скольжения по плоской поверхности со скоростью 10 м/с. масса цилиндра 153. Определить период колебаний диска радиусом R = 5 см относительно оси, проходящей через образующую диска перпендикулярно его плоскости. 154. Определить момент инерции диска радиусом R = 6 см и массой m = 3 кг относительно перпендикулярной оси, проходящей через его центр, если на диске по его диаметру вплотную лежат 3 диска радиусом r = 2 см и массой m = 0, 5 кг. 155. Определить длину горизонтального стержня массой m = 5 кг, вращающегося вместе с платформой массой М = 10 кг и радиусом R = 0, 5 м под действием силы F = 5 Н, приложенной к ободу платформы, угловое ускорение e = 1 рад/с. Система вращается относительно оси, проходящей через центры инерции тел. 156. Во сколько раз изменится частота вращения стержня массой 157. Два одинаковых груза массой m подвешены к вертикальной оси на нитях длиной l. Определить их кинетическую энергию, если они при вращении с угловой скоростью 158. Шар и сплошной цилиндр имеют одинаковую массу m = 5 кг и катятся с одинаковой скоростью V = 10 м/с. Найти кинетические энергии этих тел. 159. В тонком диске массой m = 5 кг и радиусом R = 0, 5 м вырезано n = 2 круговых отверстия радиусом r = 0, 1 м на расстояниях a = 0, 3 м от центра диска. Определить момент инерции диска относительно оси, проходящей через центр тяжести. 160. Точка колеблется гармонически по закону 161. Материальная точка совершает колебания по закону 162. Материальная точка совершает колебания по закону 163. Материальная точка одновременно участвует в двух взаимно перпендикулярных колебаниях, описываемых уравнениями 164. На тонкой нити длиной l подвешен шар радиусом r = 0, 1 l. Определить относительную погрешность в определении периода колебаний, если маятник считать математическим. 165. Точка участвует одновременно в двух гармонических колебаниях одинаковой частоты, направленных вдоль одной прямой: 166. Тело движется под действием силы 167. Амплитуда гармонического колебания равна 5 см, период 4 с, начальная фаза φ = π /4. Написать уравнение этого колебания. Найти смещение колеблющейся точки от положения равновесия при t = 0и при t = 1, 5 c. 168. Материальная точка массой 10 г колеблется согласно уравнению 169. Определить длину l математического маятника, совершающего колебания с частотой v = 0, 5 с-1. 170. Внутренняя часть шара, радиус которого R = 6 см, сделана из стали, а внешняя из пробки (r0 = 0, 2 103 кг/м3). Радиус внутренней части r = 3 см. Будет ли такой шар плавать в воде? 171. К одной из чашек рычажных весов подвешено тело плотностью r = 2, 7 103 кг/м3. Тело уравновешивается гирями весом 172. По трубопроводу, состоящему из двух труб диаметром 173. По горизонтальному суживающемуся трубопроводу протекает вода в количестве V = 30 м3/ч. Определить давление и скорость течения после сужения, если в трубе большего диаметра давление 174. Стальной шарик диаметром 4 мм падает в сосуде с жидкостью с постоянной скоростью V = 0, 2 м/с. Найти динамическую вязкость жидкости, если ее плотность r = 1, 2 103 кг/м3. 175. В цилиндрический сосуд, наполненный глицерином, бросают алюминиевый шарик диаметром d = 6 см. Определить, при какой скорости падение шарика станет равномерным. Коэффициент вязкости глицерина h = 1, 4 10-3 Нс/м2. 176. Определить время подъема движущихся с постоянной скоростью пузырьков воздуха со дна водоема глубиной 1 м. Диаметр пузырьков d = 1 мм. Коэффициент вязкости воды h = 1, 1 10-3 Нс/м2. 177. Определить скорость и ускорение стального шарика, падающего в жидкости, плотность которой rж = 1, 1 103 кг/м3, коэффициент вязкости h = 0, 5 10-3 Нс/м2. Диаметр шарика d = 1 мм. 178. По трубопроводу, состоящему из двух труб диаметрами 179. К рычажным весам одной из чашек подвешено тело плотностью r = 2, 7 103 кг/м3. Тело уравновешивается гирями весом
|

 . Найти скорость и ускорение точки через время t = 10 с после начала движения, если a = 3 м/с, b = 1 м/с2.
. Найти скорость и ускорение точки через время t = 10 с после начала движения, если a = 3 м/с, b = 1 м/с2.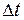 . Через сколько времени от начала движения первого тела расстояние между ними станет равным
. Через сколько времени от начала движения первого тела расстояние между ними станет равным  ?
? , где все величины выражены в системе СИ. Найти период обращения материальной точки и ее угловую скорость в конце 10 секунды.
, где все величины выражены в системе СИ. Найти период обращения материальной точки и ее угловую скорость в конце 10 секунды. в момент t = 3 с точки, находящейся на ободе колеса радиусом R= 0, 5 м, вращающегося согласно уравнению
в момент t = 3 с точки, находящейся на ободе колеса радиусом R= 0, 5 м, вращающегося согласно уравнению  , где
, где  = 2 рад/с,
= 2 рад/с,  = 0, 2 рад/с3.
= 0, 2 рад/с3. точки, лежащей на расстоянии r = 10 см от оси колеса.
точки, лежащей на расстоянии r = 10 см от оси колеса. см. Зависимость пути от времени дается уравнением
см. Зависимость пути от времени дается уравнением  , где
, где 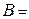 0, 1 м/с3. Найти нормальное и тангенциальное ускорение точек в момент, когда линейная скорость точки v = 0, 3 м/с.
0, 1 м/с3. Найти нормальное и тангенциальное ускорение точек в момент, когда линейная скорость точки v = 0, 3 м/с.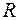 = 50 см с постоянным тангенциальным ускорением at = 5 см/с2. Через сколько времени после начала движения нормальное ускорение
= 50 см с постоянным тангенциальным ускорением at = 5 см/с2. Через сколько времени после начала движения нормальное ускорение  точки будет вдвое больше тангенциального?
точки будет вдвое больше тангенциального? = 105 кг поднимается вертикально вверх, сила тяги его двигателей
= 105 кг поднимается вертикально вверх, сила тяги его двигателей  = 3∙ 106 Н. Чему равно его ускорение?
= 3∙ 106 Н. Чему равно его ускорение? , где все величины выражены в системе СИ. Найти силу, действующую на тело в конце второй секунды движения.
, где все величины выражены в системе СИ. Найти силу, действующую на тело в конце второй секунды движения. = 11 км/с)? Считать движение ракеты равномерно-ускоренным. С какой силой будет давить брусок массой 70 кг на пол ракеты, если она будет подниматься вертикально?
= 11 км/с)? Считать движение ракеты равномерно-ускоренным. С какой силой будет давить брусок массой 70 кг на пол ракеты, если она будет подниматься вертикально? свободного падения у поверхности Земли и ее радиус
свободного падения у поверхности Земли и ее радиус  на высоте
на высоте 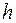 = 1000 м над поверхностью Земли.
= 1000 м над поверхностью Земли.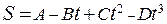 , где С = 5 м/с2, D = 1 м/с3. Найти величину силы, действующей на тело в конце первой секунды движения.
, где С = 5 м/с2, D = 1 м/с3. Найти величину силы, действующей на тело в конце первой секунды движения.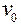 , пробивает стену толщиной b = 0, 4 м (
, пробивает стену толщиной b = 0, 4 м ( = 150 м/с. Найти время движения пули в стене, если сопротивление стены пропорционально квадрату скорости движения пули.
= 150 м/с. Найти время движения пули в стене, если сопротивление стены пропорционально квадрату скорости движения пули. ?
? = 0, 5 кН/м и
= 0, 5 кН/м и  = 1 кН/м скреплены параллельно. Определить потенциальную энергию П данной системы при абсолютной деформации
= 1 кН/м скреплены параллельно. Определить потенциальную энергию П данной системы при абсолютной деформации 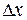 = 4 см.
= 4 см.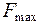 сжатия буферных пружин и продолжительность
сжатия буферных пружин и продолжительность  = 2 м/с2. Какую силу, параллельную наклонной плоскости, необходимо приложить для подъема тела. Коэффициент трения k = 0, 2, угол наклона a = 30о.
= 2 м/с2. Какую силу, параллельную наклонной плоскости, необходимо приложить для подъема тела. Коэффициент трения k = 0, 2, угол наклона a = 30о. ударяет в неупругое покоящееся тело массой
ударяет в неупругое покоящееся тело массой  . Определить, во сколько раз уменьшится кинетическая энергия тела.
. Определить, во сколько раз уменьшится кинетическая энергия тела. 2 кг движется со скоростью
2 кг движется со скоростью  = 400 м/с в направлении полета снаряда. Определить абсолютное значение и направление скорости меньшей части снаряда.
= 400 м/с в направлении полета снаряда. Определить абсолютное значение и направление скорости меньшей части снаряда. = 300 м/с. Определить скорость u2 большего осколка.
= 300 м/с. Определить скорость u2 большего осколка.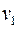 = 1 м/с и сталкивается с покоящимся шаром массой m2 = 2 кг. Определить скорости
= 1 м/с и сталкивается с покоящимся шаром массой m2 = 2 кг. Определить скорости  шаров после удара. Шары считать однородными, абсолютно упругими, удар прямым, центральным.
шаров после удара. Шары считать однородными, абсолютно упругими, удар прямым, центральным. импульса тела.
импульса тела. отклонились на угол a.
отклонились на угол a. . Найти максимальное значение скорости и ускорения. Найти зависимость ускорения от времени.
. Найти максимальное значение скорости и ускорения. Найти зависимость ускорения от времени.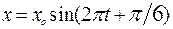 . В какой момент времени ее потенциальная энергия равна кинетической?
. В какой момент времени ее потенциальная энергия равна кинетической? . Определить силу, действующую на тело, и его максимальную кинетическую энергию.
. Определить силу, действующую на тело, и его максимальную кинетическую энергию. . Определить уравнение траектории точки.
. Определить уравнение траектории точки. . Определить амплитуду и начальную фазу результирующего колебания.
. Определить амплитуду и начальную фазу результирующего колебания. по закону
по закону  . Найти работу силы за время от
. Найти работу силы за время от  до t = t2.
до t = t2. , где A = 5 см,
, где A = 5 см,  ,
,  . Найти максимальную силу, действующую на точку и полную энергию колеблющейся точки.
. Найти максимальную силу, действующую на точку и полную энергию колеблющейся точки. . Если тело поместить в жидкость, то оно уравновешивается весом Р2 = 1/З
. Если тело поместить в жидкость, то оно уравновешивается весом Р2 = 1/З  = 0, 2 м и d2 = 0, 12 м, соответственно, соединенных последовательно, протекает вода при температуре t = 20 С в количестве V = 120 м3/ч. Давление в трубопроводе перед сужением
= 0, 2 м и d2 = 0, 12 м, соответственно, соединенных последовательно, протекает вода при температуре t = 20 С в количестве V = 120 м3/ч. Давление в трубопроводе перед сужением  . Определить давление после сужения.
. Определить давление после сужения.


