Для косвенных измерений
При косвенных измерениях искомую физическую величину
Тогда для расчета погрешности измерений можно использовать дифференциальный ( другое название логарифмический) метод, в основе которого лежит свойство натурального логарифма:
Полный дифференциал логарифма исходной функции будет равен:
где Таким образом, получаем:
Учитывая, что дифференциал независимой переменной равен ее приращению (
Значения Таким образом, для определения погрешностей косвенных измерений искомой величины ـ взять натуральный логарифм расчетной формулы; ـ продифференцировать полученное выражение; ـ произвести замену знаков дифференциала ـ знаки “минус” заменить знаками “плюс”, так как суммарная погрешность всегда больше погрешности отдельных измерений; ـ в полученную формулу подставить средние арифметические значения измеренных величин и их абсолютные погрешности; ـ рассчитать относительную ( ـ результат измерений записать в виде: Пример: Пусть в лабораторной работе требовалось определить удельное сопротивление проволоки с использованием закона Ома. Прямыми измерениями определяются сила тока
Выведем формулу для расчета погрешностей: ـ ـ ـ ـ ـ ـ ـ результат запишем в виде: Еρ =…% В таблице 1 представлены уже готовые формулы расчета погрешностей для наиболее распространенных функциональных зависимостей, выведенные с использованием логарифмического метода. Таблица 1. Формулы расчета погрешностей для некоторых функциональных зависимостей
Для расчета абсолютной погрешности измерений применяется формула:
Например, при определении количества теплоты, выделяющегося в нагревателе, с помощью закона Джоуля-Ленца в виде:
формула для расчета относительной погрешности измерения количества теплоты
Абсолютную погрешность измерений
Контрольные вопросы 1. Дайте определения терминам «измерение», «объект измерения», «метод и средства измерений». 2. Сформулируйте понятия основной и производной физических величин. 3. Что представляет собой Международная система единиц? 4. Какие измерения называются прямыми? Косвенными? 5. Что называется средством измерения, перечислите виды средств измерений. 6. Чем отличаются эталонные, рабочие и образцовые средства измерений? 7. Каковы основные виды и методы измерений? 8. Дайте определение погрешности измерений, перечислите ее виды. 9. Как рассчитать погрешность прибора по его классу точности? 10. Дайте характеристику составляющим погрешности. 11. Как рассчитываются погрешности при прямых измерениях? 12. Расскажите о расчете погрешностей при косвенных измерениях.
|

 определяют путем вычислений по результатам прямых измерений других величин. Для оценки погрешностей косвенных измерений величины
определяют путем вычислений по результатам прямых измерений других величин. Для оценки погрешностей косвенных измерений величины  . Пусть искомая величина является функцией нескольких переменных:
. Пусть искомая величина является функцией нескольких переменных: (12)
(12)

 - показатели степени аргументов
- показатели степени аргументов 

 ), и если приращение аргумента мало для функции, то дифференциал функции приблизительно равен ее приращению, то есть
), и если приращение аргумента мало для функции, то дифференциал функции приблизительно равен ее приращению, то есть  , получаем:
, получаем:
 измеряют один или несколько раз и обрабатывают по правилам оценки погрешностей прямых измерений. Если при логарифмировании и дифференцировании в выражении появились знаки «–», то для нахождения максимальной относительной погрешности их необходимо заменить на знаки «+».
измеряют один или несколько раз и обрабатывают по правилам оценки погрешностей прямых измерений. Если при логарифмировании и дифференцировании в выражении появились знаки «–», то для нахождения максимальной относительной погрешности их необходимо заменить на знаки «+». используют формулу, полученную по следующим правилам:
используют формулу, полученную по следующим правилам: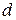 на знаки конечного приращения
на знаки конечного приращения  ;
;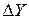 ) погрешности измерений искомой величины;
) погрешности измерений искомой величины; .
.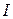 , напряжение
, напряжение  , длина
, длина  , площадь поперечного сечения проволоки через радиус
, площадь поперечного сечения проволоки через радиус 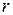 . Тогда расчетная формула будет иметь вид:
. Тогда расчетная формула будет иметь вид:
 ;
; ; (в данном случае число
; (в данном случае число  принято за постоянную);
принято за постоянную);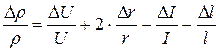 ;
;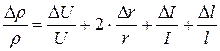 ;
; ;
; ;
; (Ом·м)
(Ом·м)
 =
= 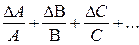
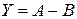








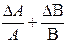








 ,
, , согласно строке 3 таблицы 1, будет иметь вид:
, согласно строке 3 таблицы 1, будет иметь вид:




