Глава 2. Емкостная и тепловая аппаратура
§ 1. Теоретическая часть Основным узлом аппарата является корпус, который определяет его форму, размеры, объем, производительность и стоимость. Корпуса аппаратов классифицируются: по форме на: цилиндрические, сферические, конические, торовые, прямоугольные и комбинированные; по схеме нагрузки на: работающие под давлением внутреннего или внешнего давления; по расположению в пространстве на вертикальные, горизонтальные и наклонные; по толщине стенки на: тонкостенные (у которых толщина стенки не превышает 10 % внутреннего диаметра, т. е. по температуре стенки на: необогреваемые, обогреваемые и охлаждаемые. Наибольшее распространение получили цилиндрические вертикальные аппараты, т.к по сравнению с горизонтальными цилиндрическими аппаратами в них исключены дополнительные напряжения при изгибе, возникающие в корпусе при действии силы тяжести аппарата и находящейся в нем среды. Выделим из рассматриваемой оболочки элемент поверхности, ограниченный двумя смежными меридиональными сечениями и двумя нормальными к меридиану сечениями (рис. 2.1).
Составляя уравнение равновесия равнодействующих сил, после ряда преобразований получаем уравнение Лапласа
Для получения второго уравнения отсечем коническим нормальным к меридиану сечением часть оболочки (рис. 2.2) и отбросим нижнюю часть. Действие отсеченных стенок заменим действующими в меридиональном направлении упругими силами
Определим радиальное перемещение образующей цилиндрической оболочки, находящейся под внутренним давлением. Из уравнений (2.1) и (2.2) находим
Уравнения (2.3) и (2.4) являются основными уравнениями безмоментной теории оболочек, исходя из которых с учетом соответствующих значений главных радиусов кривизны rt и rm получают основные расчетные зависимости для цилиндрических, конических, сферических и эллиптических оболочек. Для цилиндрического сосуда rt = r (r – радиус сосуда), r m = ¥,
Для конического сосуда rt = R к /cosa, где R к – радиус основания конической оболочки; a – половина угла раствора конуса
Из формул (2.3…2.8) видно, что при одинаковом давлении, диаметрах сосудов и толщине стенки максимальное нормальное напряжение сферической оболочки в 2 раза меньше нормального напряжения цилиндрической и в (1/cos a) раз больше конической. Определим напряжения в эллиптическом днище. Пусть полуоси эллипса будут равны D/ 2 и H. Радиусы кривизны эллипсоида в произвольной точке характеризуются уравнениями
где q – угол между нормалью и осью вращения; R0 = D/ 2 Подставляя (2.9) и (2.10) в (2.3) и (2.4), получаем
Узлы сопряжения оболочек. Полученные выше расчетные формулы выведены для случая нагружения оболочек равномерно распределенными по поверхности статическими нагрузками и справедливы для оболочек, у которых не закреплены края. В реальных конструкциях края оболочек прикрепляются к другим оболочкам (днища, крышки, люки, патрубки и т. д.). В таких узлах сопряжения возникают дополнительные, так называемые краевые, нагрузки, вызывающие местные напряжения изгиба в материале сопрягаемых элементов. Краевая сила Q 0 и краевой момент M 0 являются реакциями заделки края оболочки, которому мешает деформироваться сопрягаемая деталь. Причинами появления краевых нагрузок Q 0 и M 0 могут быть: заделка края оболочки (рис. 2.3); изменение геометрических размеров (формы) оболочки при переходе от одного сечения к другому (рис. 2.4);
Рис. 2.4. Примеры изменения геометрических размеров оболочки: а – соединение цилиндрических обечаек разной толщины; б, в, г – соединения обечаек разной формы
3) изменение нагрузки при переходе от одного сечения к другому (рис. 2.5);
Рис. 2.5. Примеры изменения нагрузок, действующих на оболочки: а – соединение корпуса аппарата с его рубашкой; б – соединение оболочки с опорой
4) изменение свойств материала (модуля упругости Е, коэффициента линейного расширения a, коэффициента Пуассона m и др.) при переходе от одного сечения к другому (рис. 2.6).
где Укрепление отверстий в оболочках. В аппаратах выполняются отверстия для присоединения трубопроводов, установки лазов, смотровых люков и т. д. Отверстия не только уменьшают несущую площадь материала корпуса, механически ослабляя конструкцию, но и вызывают высокую концентрацию напряжений вблизи края отверстия. Повышенные напряжения в области отверстий снимаются двумя способами: 1) увеличением толщины стенки всей оболочки исходя из максимальных напряжений у края отверстия – нерационален, т. к. область повышенных напряжений незначительна и ограничивается диаметром
где d – диаметр отверстия; D p – расчетный диаметр оболочки; S – толщина стенки; с – прибавка на коррозию. 2) укреплением края отверстия добавочным материалом, применением специальных колец, привариваемых к стенке аппарата, или усилением патрубка. Наибольшее распространение получил так называемый геометрический критерий укрепления, предусматривающий компенсацию площади продольного сечения выреза с помощью дополнительных укрепляющих элементов, расположенных в зоне укрепления.
Условие укрепления имеет вид
где A – площадь продольного сечения выреза, подлежащая компенсации, A 0 – площадь продольного сечения оболочки, участвующая в укреплении; A 2 – площадь продольного сечения усиливающего обечайку элемента в зоне укрепления; A 1 Н и A 1 B – площади продольного сечения соответственно наружной и внутренней частей штуцера, участвующие в укреплении, Степень концентрации напряжений у неукрепленных круговых вырезов определяется геометрическими соотношениями между размерами отверстия и аппарата. Для цилиндрических оболочек концентрация напряжений в области круговых вырезов возрастает с увеличением отношения радиуса выреза к радиусу обечайки (r отв /R аппар.) и уменьшением отношения толщины стенки обечайки S к ее радиусу R аппар. Укрепления можно разделить на две группы: 1) с патрубками, примыкающими к корпусу (рис. 2.7, а, б, в, г); 2) с патрубками, пропущенными через стенку (рис. 2.7 д).
Рис. 2.7. Укрепление круговых вырезов корпусов аппаратов: а – примыкающим патрубком; б – примыкающим патрубком и накладкой; в – сварным кольцом и примыкающим патрубком; г – примыкающим патрубком с коническим переходом; д – сквозным патрубком и сварным кольцом Последние более эффективны, т. к. усиливается поверхность корпуса для которой характерна наибольшая концентрация напряжения. Расчет толщины стенки обечайки. Толщина стенки цилиндрического аппарата, находящегося под внутренним давлением, определяется по формуле
где Формула (2.16) применима при расчете тонкостенных цилиндрических аппаратов, т.е. при выполнении условия:
Аналогично толщина стенки определяется – для конических оболочек
где – для сферической оболочки
если
где – для эллиптического днища
если
– для плоских днищ и крышек
где Расчет аппаратов на устойчивость. Потеря устойчивости – это резкое качественное изменение характера деформации элемента конструкции, происходящее при определенном значении нагрузки. Причины потери устойчивости тонкостенных оболочек: действие изгибающего момента При совместном их действии условие устойчивости имеет вид:
где
где
Нагрузку, при которой происходит потеря устойчивости, называет критической. Длина, по которой цилиндрические оболочки делятся на короткие и длинные, определяется по формуле:
Если расчетная длина неподкрепленной кольцами жесткости обечайки Фланцевым соединением (рис. 2.8) называется особый вид разъемных соединений, состоящий из двух фланцев, болтов и прокладки, которая устанавливается между фланцами и обеспечивает необходимую герметичность и прочность конструкции при относительно небольшом усилии затяжки болтов.
– резьбовые; – свободные, у которых корпус аппарата разгружен от действия изгибающих моментов, возникающих при затяжке фланцевого соединения; – цельные, когда корпус аппарата и фланец работают под нагрузкой совместно. Выбор конструкции фланцев определяется, в основном, тремя факторами: а) величиной рабочего давления; б) трудоемкостью и периодичностью сборки-разборки соединения; в) стоимостью изготовления и характером обслуживания соединения. Наибольшее распространение в пищевом машиностроении получили два типа цельных фланцев: – плоские приварные фланцы (рис. 2.9, а), представляющие собой плоские кольца, приваренные к трубе по ее периметру. Они применяются при давлении 0, 3…1, 6 МПа и температуре до 300 оС; – фланцы приварные встык (рис. 2.9, б), имеющие конические втулки-шейки, которые привариваются стыковым швом к патрубку. Они применяются при давлении от 1, 0 до 16, 0 МПа.
Рис. 2.9. Типы фланцев: а – плоский приварной; б – приварной встык; в – свободный
Свободные фланцы (рис. 2.9, в) представляют собой кольца, свободно надеваемые на соединяемые патрубки, на концах которых имеется отбортовка или приваренное кольцо. Они используются при давлении до 1, 6 МПа и температуре до 300 оС, а число циклов нагружения не должно превышать 2000. Уплотнительные поверхности фланцевых соединений могут быть следующих типов: – плоская уплотнительная поверхность (рис. 2.10, а). Применяется при внутреннем давлении до 0, 6 МПа; – «выступ – впадина» (рис. 2.10, б). Используются при внутренним давлении P = 0, 6…1, 6 МПа; – «шип – паз» (рис. 2.10, в). Рекомендуется при P = 1, 6…6, 4 МПа; – уплотнительная поверхность под металлическую прокладку (рис. 2.10, г) – при P = 6, 4…16 МПа.
Рис. 2.10. Типы уплотнительных поверхностей фланцевых соединений: а – гладкая уплотнительная поверхность; б – «выступ-впадина»; в – «шип-паз»; г – под металлическую прокладку
В качестве прокладок применяют следующие материалы: металлы (свинец, медь, алюминий, никель); полимеры (фторопласт, полиэтилен, асбест, паронит, резина, полихлорвинил); бумагу, картон, кожу, комбинированные прокладки и др. Они должны сохранять герметичность соединения при упругих перемещениях элементов фланцевого соединения; заполнять все микронеровности уплотнительных поверхностей при сжатии с малым давлением; обеспечивать долговечность и надежность соединения при его длительной эксплуатации в условиях воздействия коррозионных сред при высоких и низких температурах. Расчет фланцевого соединения заключается в определении геометрических размеров его основных элементов и в удовлетворении условиям герметичности и прочности. § 2. Расчетно-проектная работа № 1.
|

 и
и  не более 10 МПа) и толстостенные;
не более 10 МПа) и толстостенные;  Обозначим радиусы кривизны дуги меридиана (rm) и сечения, перпендикулярного к дуге меридиана (rt), толщину стенки S и размеры элемента в меридиональном и окружном (кольцевом) направлениях через dSm и dSt. На гранях элемента возникают меридиональные sm и окружные st напряжения. Напряжения sm и st, умноженные на соответствующие площади граней элементов, дадут силы smSdSt и stSdSm (рис. 2.1).
Обозначим радиусы кривизны дуги меридиана (rm) и сечения, перпендикулярного к дуге меридиана (rt), толщину стенки S и размеры элемента в меридиональном и окружном (кольцевом) направлениях через dSm и dSt. На гранях элемента возникают меридиональные sm и окружные st напряжения. Напряжения sm и st, умноженные на соответствующие площади граней элементов, дадут силы smSdSt и stSdSm (рис. 2.1). . (2.1)
. (2.1) Однако одного уравнения Лапласа недостаточно для определения st и sm.
Однако одного уравнения Лапласа недостаточно для определения st и sm. . (2.2)
. (2.2) ; (2.3)
; (2.3) (2.4)
(2.4) ; (2.5)
; (2.5)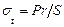 . (2.6)
. (2.6) ; (2.7)
; (2.7) . (2.8)
. (2.8) , (2.9)
, (2.9) (2.10)
(2.10) – радиус кривизны в вершине (при q = 0), g= [ (D/ 2 )2-H2 ]
– радиус кривизны в вершине (при q = 0), g= [ (D/ 2 )2-H2 ]  – параметр, определяющий форму эллипса.
– параметр, определяющий форму эллипса. , (2.11)
, (2.11) . (2.12)
. (2.12)


 Для определения Qo и Mo составляются так называемые уравнения совместности радиальных D p и угловых qp деформаций. Сущность этих уравнений заключается в том, что для нормальной работы аппарата в узле сопряжения не должно быть никаких относительных перемещений сопрягаемых деталей, т.е. необходимо выполнение условий, когда суммы радиальных D p и угловых qp деформаций края одной детали от действующих внешних и краевых нагрузок равны соответствующим суммам радиальных и угловых деформаций края другой детали от действующих на нее активных и реактивных нагрузок. Приняв для края оболочки положительными радиальные перемещения D в направлении от ее оси, а угловые перемещения q в направлении по часовой стрелке, получим для правой части оболочек уравнения совместности радиальных и угловых деформаций:
Для определения Qo и Mo составляются так называемые уравнения совместности радиальных D p и угловых qp деформаций. Сущность этих уравнений заключается в том, что для нормальной работы аппарата в узле сопряжения не должно быть никаких относительных перемещений сопрягаемых деталей, т.е. необходимо выполнение условий, когда суммы радиальных D p и угловых qp деформаций края одной детали от действующих внешних и краевых нагрузок равны соответствующим суммам радиальных и угловых деформаций края другой детали от действующих на нее активных и реактивных нагрузок. Приняв для края оболочки положительными радиальные перемещения D в направлении от ее оси, а угловые перемещения q в направлении по часовой стрелке, получим для правой части оболочек уравнения совместности радиальных и угловых деформаций: , (2.13)
, (2.13)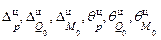 – соответственно радиальные и угловые деформации края цилиндрической обечайки под действием нагрузок p, Q 0 и M 0;
– соответственно радиальные и угловые деформации края цилиндрической обечайки под действием нагрузок p, Q 0 и M 0;  – соответственно радиальные и угловые деформации сферической оболочки под действием нагрузок p, Q, Q 0и M 0.
– соответственно радиальные и угловые деформации сферической оболочки под действием нагрузок p, Q, Q 0и M 0. , (2.14)
, (2.14) , (2.15)
, (2.15) и
и  – соответственно отношение допускаемого напряжения материала штуцера и усиливающего элемента к допускаемому напряжению материала укрепляемой оболочки.
– соответственно отношение допускаемого напряжения материала штуцера и усиливающего элемента к допускаемому напряжению материала укрепляемой оболочки.
 , (2.16)
, (2.16) – внутреннее давление, МПа;
– внутреннее давление, МПа;  – внутренний диаметр цилиндрического аппарата, м;
– внутренний диаметр цилиндрического аппарата, м;  – коэффициент прочности сварного шва
– коэффициент прочности сварного шва  ;
;  – допускаемое напряжение на растяжение для материала аппарата, МПа;
– допускаемое напряжение на растяжение для материала аппарата, МПа;  – прибавка на коррозию (с =(1…3)∙ 103 м), м;
– прибавка на коррозию (с =(1…3)∙ 103 м), м;  – прибавка на округление размера до стандартного значения толщины листового проката, м.
– прибавка на округление размера до стандартного значения толщины листового проката, м. . (2.17)
. (2.17) , если
, если , (2.18)
, (2.18) – половина угла при вершине конуса
– половина угла при вершине конуса 

 , (2.19)
, (2.19) – внутренний диаметр сферической оболочки, м;
– внутренний диаметр сферической оболочки, м;
 , (2.20)
, (2.20) , (2.21)
, (2.21) – коэффициент, учитывающий тип закрепления днища (
– коэффициент, учитывающий тип закрепления днища ( =0, 38…0, 53);
=0, 38…0, 53);  – коэффициент ослабления.
– коэффициент ослабления. , осевой сжимающей силы
, осевой сжимающей силы  или наружного давления среды
или наружного давления среды  .
. , (2.22)
, (2.22) – допускаемое значение осевой сжимающей силы для цилиндрических оболочек,
– допускаемое значение осевой сжимающей силы для цилиндрических оболочек, ; (2.23)
; (2.23) – допускаемый изгибающий момент для цилиндрических обечаек,
– допускаемый изгибающий момент для цилиндрических обечаек, (2.24)
(2.24) ,
,  – соответственно расчетное и допускаемое наружное давление, для цилиндрических обечаек,
– соответственно расчетное и допускаемое наружное давление, для цилиндрических обечаек, . (2.25)
. (2.25) . (2.26)
. (2.26) , то оболочка является длинной, а при
, то оболочка является длинной, а при  – короткой.
– короткой. Фланцы классифицируются по конструкции на:
Фланцы классифицируются по конструкции на:




