Показатели ремонтопригодности и сохраняемостиСреднее время восстановления работоспособного состояния. Вероятность восстановления работоспособного состояния в заданное время. Средний и гамма-процентный сроки сохраняемости. Комплексные показатели включают в себя: – коэффициент технического использования k ти
где T раб – время работы машины за некоторый период эксплуатации; – коэффициент готовности k г
где T р.с – время нахождения машины в работоспособном состоянии за некоторый период эксплуатации; – коэффициент долговечности k д
где Тi – срок службы (наработка) до i- ого отказа; ti – продолжительность (трудоемкость) i- ого отказа. Общие зависимости. Рассмотрим эксплуатацию числа N элементов в течение времени t. Пусть к концу срока эксплуатации остается N p работоспособных и n отказавших элементов. В этом случае относительное количество отказов Q(t)
Если N достаточно велико, то Q(t) можно рассматривать как вероятность отказа. Тогда вероятность безотказной работы P(t)
Из (1.5) следует, что P(t) + Q(t) = 1. (1.6) Распределение отказов во времени характеризуется функцией плотности распределения f(t) наработки до отказа:
При этом вероятности отказов и безотказной работы в функции плотности f(t) выражаются зависимостями
и Интенсивность отказов l(t)
Перепишем (1.10) в виде
Интегрируя (1.11), получаем
Рис. 1.1. Интенсивность отказов машины в процессе ее эксплуатации
Уравнение (1.12) является одним из основных уравнений теории надежности. В процессе эксплуатации изделия можно выделить три периода (рис. 1.1): I – приработка, II – нормальная эксплуатация; III – износовые (постепенные) отказы. Надежность в период нормальной эксплуатации. В этот период отказы имеют постоянную интенсивность, т. к. износовые (постепенные) отказы еще не проявляются, а имеют место только внезапные отказы, т. е.
где m t – средняя наработка до отказа, ч. Вероятность безотказной работы
подчиняется экспоненциальному закону распределения времени t безотказной работы и одинакова за любой одинаковый промежуток времени (рис. 1.2).
Плотность распределения в общем случае
Надежность в период постепенных (износовых) отказов. Для постепенных отказов целесообразно использовать такие законы распределения времени безотказной работы, которые дают вначале низкую плотность распределения, затем максимум и далее падение, связанное с уменьшением числа работоспособных элементов. Для описания износовых отказов в теории надежности применяют: нормальное усеченное нормальное и логарифмически нормальное распределения, а также распределение Вейбулла (табл. 1.1). Надежность в период совместного действия внезапных и постепенных отказов. Вероятность безотказной работы машины в период совместного действия внезапных и постепенных отказов по теореме умножения вероятностей определяется по формуле
где P в (t)=е-lt и P п (t)=P п (T+t)/P п (t) – соответственно вероятности отсутствия внезапных и постепенных отказов, T – время наработки на отказ, t – продолжительность работы машины за некоторый период эксплуатации.
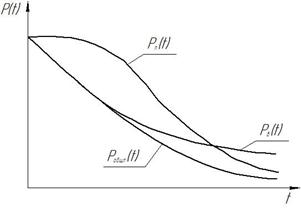
Рис. 1.3. Кривые вероятности безотказной работы P общ ( t) при совместном действии внезапных P в ( t) и постепенных P п ( t) отказов
Анализ кривых на рис. 1.3. показывает, что в период постепенных отказов их интенсивность значительно выше, чем в период внезапных отказов. Основные пути повышения надежности машин: 1. Повышение сопротивляемости машин внешним воздействиям (создания более прочных, износостойких машин, уменьшение нагрузок, применение упрочняющей технологии и т. д.). 2. Изоляция машин от вредных воздействий (установка машин на фундаменты, применение антикоррозионных покрытий, защита от пыли, грязи, вибро- и звукоизоляция и т. д.). 3. Создание оптимальной конструкции машины. 4. Применение автоматики для повышения надежности машин. 5. Создание машин с регламентированными показателями надежности.
Таблица 1.1
|
, (1.1)
– суммарная продолжительность ремонтов машины за тот же период;
, (1.2)
– суммарная продолжительность внеплановых ремонтов за тот же период;
, (1.3)
. (1.4)
. (1.5)
. (1.7)
(1.8)
. (1.9)
. (1.10)
. (1.11)
или 
. (1.12)
, (1.13)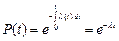
, (1.14)
Существенным достоинством экспоненциального распределения является его простота: оно имеет только один параметр.
(1.15)
, (1.16)
