Теоретическая часть. Важной особенностью ротационных машин является наличие рабочих органов, вращающихся с большой частотой
Важной особенностью ротационных машин является наличие рабочих органов, вращающихся с большой частотой, вследствие чего осуществляется воздействие на обрабатываемый продукт. К ротационным машинам, получившим широкое распространение в пищевой промышленности, относятся дисковые измельчители, центробежные насосы, резательные машины, молотковые дробилки, дисковые распылители в распылительных сушилках и т. п. Основные рабочие органы этого разнообразного оборудования – быстровращающийся диск или набор дисков простого или сложного профиля (рис. 5.1), лопасти, крыльчатки, ножи.
Рис. 5.1. Конструктивные формы быстровращающихся дисков: а – постоянной толщины; б – конический; в – гиперболический; г – сложного профиля
Диски постоянной толщины (рис. 5.1, а) нагружены по внутренней поверхности радиуса R 1 радиальным напряжением σ r1, возникающим от посадки диска с натягом на вал, а по наружной поверхности радиуса R 2 – радиальнымнапряжением
где
здесь Обычно
где
Рис. 5.2. Расчетная схема диска постоянной толщины
В конических дисках (рис. 5.1, б) напряжения В гиперболических дисках (рис. 5.1 в) необходимо в начале определить показатель гиперболы
Затем через коэффициенты При расчете дисков сложного профиля (рис. 5.1, г) пользуются методом аппроксимации, когда реальный сложный профиль диска условно заменяют участками постоянной толщины, с последовательным применением к каждому i – му участку уравнений (5.1, 5.2), связывающих между собой напряжения
где коэффициенты α и β зависящие от
Так как на i -м радиусе происходит «скачок» толщины b (рис. 5.3), то напряжения
полученными соответственно из условия равенства радиальных сил и равенства радиальных напряжений на границе изменения толщины диска. Использование метода двух расчетов позволяет удовлетворить заданным граничным условиям
Рис. 5.3. Расчетная схема диска сложного профиля с его аппроксимацией участками постоянной толщины
Расчет диска заканчивается определением истинных напряжений
где индексы I и II обозначают соответственно первый и второй расчет; k – поправочный коэффициент. По формулам 5.12 и 5.13 строят эпюры радиальных и окружных напряжений и выявляют наиболее нагруженные участки диска. Наиболее типичным примером нагруженного диска является диск молотковой дробилки (рис. 5.4), которая применяется для разрушения хрупких материалов (зерна, сахара, соли, кости и т. п.) Разрушение частиц продукта происходит при ударе молотка, ударе частицы о зубчатую гребенку, укрепленную на корпусе дробилки, и за счет истирания. На молотковых дробилках получают относительно измельченный продукт со степенью измельчения 20...40, не требующий применения сортировочных устройств. Наиболее распространены дробилки со свободно подвешенными молотками. Рабочим органом дробилки является ротор (рис. 5.4).
Рис. 5.4. Ротор молотковой дробилки и расчетная схема его однопролетного вала: 1 – вал; 2 – ось; 3 – диск; 4 – молоток; 5 – втулка; 6 – подшипник На валу ротора 1 собран пакет из дисков 3 и втулок 5. С одной стороны пакет поджат гайкой. Молотки 4 устанавливаются между дисками на осях 2, фиксируемых от осевого смещения. Молотки подвешиваются на оси с гарантированным зазором и располагаются по окружности диска с постоянным угловым шагом. Вал ротора, диски, оси и втулки изготавливаются из конструкционных сталей; молотки из легированной термически обработанной стали (сталь 30 ХГСА). При конструировании молотковых дробилок необходимо обеспечить условия виброустойчивости. С целью уменьшения инерционных сил вследствие неуравновешенности ротора необходимо точное выполнение геометрической формы деталей. При встрече частиц продукта с концами молотков происходит удар, передаваемый на корпус. Для снижения ударных взаимодействий молотки должны быть уравновешены на удар.
|


 , возникающим от центробежного воздействия лопаток, молотков и т. п. Учитывая, что изгиб диска от вибрации и внешних нагрузок мал, температура по радиусу и толщине диска постоянна, напряжения
, возникающим от центробежного воздействия лопаток, молотков и т. п. Учитывая, что изгиб диска от вибрации и внешних нагрузок мал, температура по радиусу и толщине диска постоянна, напряжения  и
и  ; (5.1)
; (5.1) ; (5.2)
; (5.2) ; (5.3)
; (5.3) ; (5.4)
; (5.4) ; n – частота вращения диска, об/мин; r – текущий радиус диска, м;
; n – частота вращения диска, об/мин; r – текущий радиус диска, м;  ,
,  ,
, 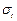 – радиальные и окружные напряжения на внутреннем и текущем радиусах, МПа.
– радиальные и окружные напряжения на внутреннем и текущем радиусах, МПа. ; (5.5)
; (5.5) – суммарная центробежная сила по наружному контуру R 2 от действия лопаток, молотков и т.п.
– суммарная центробежная сила по наружному контуру R 2 от действия лопаток, молотков и т.п.
 . (5.6)
. (5.6) и
и  по номограмме [14, 17] находят коэффициенты α и β. Дальнейший расчет гиперболического диска полностью аналогичен расчету диска постоянной толщины. Значения максимальных окружных напряжений гиперболических дисков еще меньше, чем конических, при одинаковых окружных скоростях и внешних нагрузках. Поэтому они нашли широкое применение (крыльчатки насосов и компрессоров), несмотря на сложность изготовления гиперболического профиля.
по номограмме [14, 17] находят коэффициенты α и β. Дальнейший расчет гиперболического диска полностью аналогичен расчету диска постоянной толщины. Значения максимальных окружных напряжений гиперболических дисков еще меньше, чем конических, при одинаковых окружных скоростях и внешних нагрузках. Поэтому они нашли широкое применение (крыльчатки насосов и компрессоров), несмотря на сложность изготовления гиперболического профиля. и
и  в начале (радиус ri) участка с напряжениями
в начале (радиус ri) участка с напряжениями  ,
,  в конце (радиус ri +1) участка
в конце (радиус ri +1) участка ; (5.7)
; (5.7) , (5.8)
, (5.8) , определяются по уравнениям (5.3), а сомножитель
, определяются по уравнениям (5.3), а сомножитель ; (5.9)
; (5.9) ,
,  в конце (i -1)-го участка связаны с напряжениями
в конце (i -1)-го участка связаны с напряжениями  ; (5.10)
; (5.10) , (5.11)
, (5.11) и
и 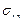 [14, 17].
[14, 17].
 ,
,  на любом радиусе ri по формулам
на любом радиусе ri по формулам ; (5.12)
; (5.12) , (5.13)
, (5.13)



