Расчет молотковой дробилки
Цель работы: 1) определение размеров конструктивных элементов молотков;
2) приобретение практических навыков расчета диска молотковой дробилки на прочность; построение эпюр радиальных  и тангенциальных и тангенциальных 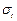 напряжений в диске молотковой дробилки; определение местного коэффициента запаса прочности; напряжений в диске молотковой дробилки; определение местного коэффициента запаса прочности;
3) расчет вала ротора дробилки на виброустойчивость.
З а д а н и е: выполнить прочностной расчет дисков молотковой дробилки и построить эпюры радиальных  и тангенциальных и тангенциальных 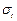 напряжений, если задано: количество молотков n 1; количество осей n 2; количество дисков n 3; длина молотка A, м; ширина молотка В, м; толщина молотка δ, м; радиус вала ротора r 1, м; радиус окружности крепления осей молотка r отв, м; толщина диска b, м; наружный диаметр диска D, м; диаметр оси подвеса молотков d ос, м; длина оси l ос, м; расстояние между опорами L, м; окружная скорость крайней точки молотка напряжений, если задано: количество молотков n 1; количество осей n 2; количество дисков n 3; длина молотка A, м; ширина молотка В, м; толщина молотка δ, м; радиус вала ротора r 1, м; радиус окружности крепления осей молотка r отв, м; толщина диска b, м; наружный диаметр диска D, м; диаметр оси подвеса молотков d ос, м; длина оси l ос, м; расстояние между опорами L, м; окружная скорость крайней точки молотка  , м/с; радиальное напряжение на поверхности посадочного отверстия диска σ r 1, МПа. , м/с; радиальное напряжение на поверхности посадочного отверстия диска σ r 1, МПа.
Методика расчета
Конструктивные размеры элементов молотка должны обеспечивать уравновешенность его на удар [14, 26].
Расстояние от центра массы молотка до оси отверстия c, м (рис. 5.5)
 . (5.14) . (5.14)
Квадрат радиуса инерции молотка относительно его центра массы 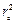 , м2 , м2
 . (5.15) . (5.15)
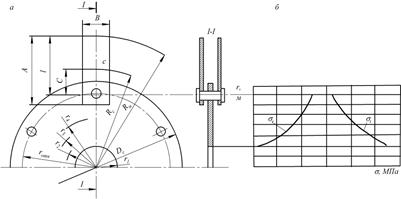
Рис. 5.5. Диск молотковой дробилки:
а – эскиз; б – эпюры напряжений σ r и 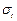
Расстояние от конца молотка до оси его подвеса l, м
 . (5.16) . (5.16)
Квадрат радиуса инерции молотка относительно оси подвеса r 2, м2
 . (5.17) . (5.17)
Конструктивные размеры молотка должны удовлетворять условию
 . (5.18) . (5.18)
Радиус центра масс молотка, м
 . (5.19) . (5.19)
Радиус крайней точки молотка, м
 . (5.20) . (5.20)
Масса молотка, кг
 . (5.21) . (5.21)
При работе молотковой дробилки в диске возникают радиальные  и тангенциальные и тангенциальные 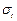 напряжения, величина которых зависит от текущего значения расчетного радиуса r (рис. 5.5). Диск молотковой дробилки можно привести к расчетной схеме диска постоянной толщины, нагруженного по радиусу r отв установки осей крепления молотков радиальным напряжением напряжения, величина которых зависит от текущего значения расчетного радиуса r (рис. 5.5). Диск молотковой дробилки можно привести к расчетной схеме диска постоянной толщины, нагруженного по радиусу r отв установки осей крепления молотков радиальным напряжением  , обусловленным центробежной силой инерции молотков и осей. , обусловленным центробежной силой инерции молотков и осей.
Угловая частота вращения ротора, с-1
 , (5.22) , (5.22)
где R 0 – радиус наиболее удаленной от оси ротора точки молотка, м.
Масса оси подвеса молотков, кг
 . (5.23) . (5.23)
Делаем допущение, что радиальные напряжения по кольцевому сечению  при радиусе r = r отв равномерно распределены по кольцевому сечению диска. при радиусе r = r отв равномерно распределены по кольцевому сечению диска.
При числе дисков n 3 ≤ 2 напряжение  , МПа, определяется по зависимости , МПа, определяется по зависимости
 ; (5.24) ; (5.24)
при n 3 > 2
 . (5.25) . (5.25)
Значения σ r 1 и 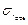 являются граничными условиями, позволяющими определить тангенциальное напряжение являются граничными условиями, позволяющими определить тангенциальное напряжение  при r = r 1 на поверхности посадочного отверстия диска. при r = r 1 на поверхности посадочного отверстия диска.
Примите r = r отв. Определим расчетные коэффициенты по зависимостям [14, 17]
 (5.26) (5.26)
 , (5.27) , (5.27)
где  – частота вращения ротора дробилки, об/мин. – частота вращения ротора дробилки, об/мин.
Рассчитаем  , МПа, по формуле , МПа, по формуле
 , (5.28) , (5.28)
где  , T – расчетные коэффициенты при r = r отв. , T – расчетные коэффициенты при r = r отв.
Разделите участок диска  на N участков (рис. 5.5, а) и определим текущие значения радиуса r, м. Рекомендуемое значение N = 5. на N участков (рис. 5.5, а) и определим текущие значения радиуса r, м. Рекомендуемое значение N = 5.
Тогда
 (5.29) (5.29)
Округлим значения расчетных радиусов.
Определим радиальные σ r, МПа, и тангенциальные σ t, МПа, напряжения при радиусах r = r 1, r 2, …, rN, r отв по зависимостям
 ; (5.30) ; (5.30)
 , (5.31) , (5.31)
где   – расчетные коэффициенты; определяются по вышеприведенным зависимостям (5.26) и (5.27). – расчетные коэффициенты; определяются по вышеприведенным зависимостям (5.26) и (5.27).
Результаты расчетов удобно представить в табличной форме (табл. 5.1).
Таблица 5.1
Сводная таблица расчетных параметров
| r, мм
| x = r 1/ r
| α r
| α t
| α c
| T
| α rσ r 1
| α tσ t 1
| α cT
| σ r, МПа
| | r 1
|
|
|
|
|
|
|
|
|
| | r 2
|
|
|
|
|
|
|
|
|
| | …
|
|
|
|
|
|
|
|
|
| | r отв
|
|
|
|
|
|
|
|
|
| | r, мм
| x = r 1/ r
| β r
| β t
| β c
| T
| β rσ r 1
| β tσ t 1
| β cT
| σ t, МПа
| | r 1
|
|
|
|
|
|
|
|
|
| | r 2
|
|
|
|
|
|
|
|
|
| | …
|
|
|
|
|
|
|
|
|
| | r отв
|
|
|
|
|
|
|
|
|
| На основании полученных значений σ r и σ t при различных значениях расчетного радиуса r построим эпюру напряжений по радиусу диска (рис. 5.5, б) и определим максимальное напряжение σ max.
Рассчитаем местный коэффициент запаса прочности для наиболее нагруженного сечения n м
 ; (5.32) ; (5.32)
где σ т– предел текучести материала диска, МПа.
Сравним местный коэффициент запаса прочности  с допускаемым с допускаемым  . В случае, если . В случае, если  , измените исходные данные, пользуясь рекомендациями: , измените исходные данные, пользуясь рекомендациями:
– при уменьшении угловой частоты вращения ротора ω необходимо увеличить радиус крайней точки молотка, чтобы окружная скорость  не изменялась; не изменялась;
– в случае, если  незначительно больше допускаемого незначительно больше допускаемого 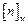 , рекомендуется увеличить ширину диска b или выбрать материал диска с большим пределом текучести. , рекомендуется увеличить ширину диска b или выбрать материал диска с большим пределом текучести.
При расчете ротора молотковой дробилки на виброустойчивость в качестве расчетной схемы принимаем стержень на двух шарнирных опорах с равномерно распределенной нагрузкой, обусловленной действием размещенных по длине вала однотипных конструктивных элементов одинаковой массы (см. рис. 5.4).
Линейная масса ротора тL, кг/м
 , (5.33) , (5.33)
где  – соответственно массы вала, молотка, оси, диска и втулки, кг; – соответственно массы вала, молотка, оси, диска и втулки, кг;  – количество втулок; d =2 r 1 – диаметр вала ротора, м; l вт = 0, 005 + δ – длина втулки, м; d вт =2 r 1 + 0, 012 – наружный диаметр втулки, м. – количество втулок; d =2 r 1 – диаметр вала ротора, м; l вт = 0, 005 + δ – длина втулки, м; d вт =2 r 1 + 0, 012 – наружный диаметр втулки, м.
Момент инерции вала ротора J, м4
 . (5.34) . (5.34)
Критическая угловая частота вращения ротора, с-1
 , (5.35) , (5.35)
где Е – модуль упругости материала вала, Н/м2 (для стали Е = 2, 1·1011 Н/м2).
Проверим условие виброустойчивости ротора
 . (5.36) . (5.36)
При невыполнении условия виброустойчивости проанализируйте формулы и выявите значимость параметров на  . На основании этого анализа измените исходные данные и расчет повторите. . На основании этого анализа измените исходные данные и расчет повторите.
Порядок оформления отчета. Отчет о расчетно-проектной работе включает в себя следующие разделы:
– цель работы;
– теоретическую часть, в которой приводятся описание конструкции молотковой дробилки, классификация дисков, особенности их прочностного расчета;
– расчетную часть, в которой дается расчет элементов молотковой дробилки по предлагаемому варианту (табл. 5.2);
– графическую часть, содержащую чертеж диска и спецификацию к нему.
| №
вар.
| n 1
| n 2
| n 3
| A, м
| B, м
| δ, м
| r 1, м
| r отв, м
| b, м
| D, м
| d ос, м
| l ос, м
| L, м
|  ,
м/с ,
м/с
|  , МПа , МПа
| |
|
|
|
| 0, 08
| 0, 04
| 0, 02
| 0, 03
| 0, 25
| 0, 01
| 0, 53
| 0, 012
| 0, 06
| 0, 2
|
|
| |
|
|
|
| 0, 09
| 0, 04
| 0, 02
| 0.039
| 0, 26
| 0, 01
| 0, 55
| 0, 012
| 0, 06
| 0, 2
|
| -5
| |
|
|
|
| 0, 10
| 0, 04
| 0, 02
| 0.034
| 0, 27
| 0, 012
| 0, 57
| 0, 012
| 0, 06
| 0, 2
|
| -10
| |
|
|
|
| 0, 11
| 0, 05
| 0, 022
| 0, 036
| 0, 28
| 0, 014
| 0, 594
| 0, 014
| 0, 07
| 0, 21
|
| -15
| |
|
|
|
| 0, 12
| 0, 05
| 0, 024
| 0, 038
| 0, 29
| 0, 014
| 0, 614
| 0, 014
| 0, 072
| 0, 21
|
|
| |
|
|
|
| 0, 13
| 0, 05
| 0, 026
| 0, 04
| 0, 3
| 0, 016
| 0, 634
| 0, 014
| 0, 074
| 0, 21
|
| -5
| |
|
|
|
| 0, 14
| 0, 06
| 0, 028
| 0, 042
| 0, 31
| 0, 016
| 0, 656
| 0, 016
| 0, 124
| 0, 24
|
| -10
| |
|
|
|
| 0, 15
| 0, 07
| 0, 03
| 0.044
| 0, 32
| 0, 018
| 0, 676
| 0, 016
| 0, 128
| 0, 24
|
| -15
| |
|
|
|
| 0, 16
| 0, 08
| 0, 032
| 0, 046
| 0, 33
| 0, 018
| 0, 696
| 0, 016
| 0, 130
| 0, 24
|
|
| |
|
|
|
| 0, 10
| 0, 05
| 0, 02
| 0, 048
| 0, 25
| 0, 01
| 0, 532
| 0, 012
| 0, 168
| 0, 29
|
| -5
| |
|
|
|
| 0, 11
| 0, 06
| 0, 022
| 0, 05
| 0, 26
| 0, 01
| 0, 552
| 0, 012
| 0, 176
| 0, 3
|
| -10
| |
|
|
|
| 0, 12
| 0, 07
| 0, 024
| 0, 052
| 0, 27
| 0, 012
| 0, 572
| 0, 012
| 0, 23
| 0, 36
|
| -15
| |
|
|
|
| 0, 13
| 0, 08
| 0, 026
| 0, 054
| 0, 28
| 0, 014
| 0, 594
| 0, 014
| 0, 24
| 0, 36
|
|
| |
|
|
|
| 0, 14
| 0, 05
| 0, 028
| 0, 056
| 0, 29
| 0, 014
| 0, 614
| 0, 014
| 0, 22
| 0, 34
|
| -5
| |
|
|
|
| 0, 15
| 0.06
| 0, 03
| 0, 058
| 0, 3
| 0, 016
| 0, 634
| 0, 014
| 0, 254
| 0, 37
|
| -10
| |
|
|
|
| 0, 16
| 0, 07
| 0, 032
| 0, 06
| 0, 31
| 0, 016
| 0, 654
| 0, 016
| 0, 31
| 0, 45
|
| -15
| |
|
|
|
| 0, 10
| 0, 08
| 0, 02
| 0, 062
| 0, 25
| 0, 018
| 0, 536
| 0, 016
| 0, 25
| 0, 39
|
|
| |
|
|
|
| 0, 11
| 0, 05
| 0, 022
| 0, 064
| 0, 26
| 0, 018
| 0, 556
| 0, 016
| 0, 254
| 0, 39
|
| -5
| |
|
|
|
| 0, 12
| 0, 06
| 0, 024
| 0, 066
| 0, 27
| 0, 01
| 0, 572
| 0, 012
| 0, 31
| 0, 44
|
| -10
| |
|
|
|
| 0, 13
| 0, 07
| 0, 026
| 0, 068
| 0, 28
| 0, 012
| 0, 592
| 0, 012
| 0, 31
| 0, 44
|
| -15
| |
|
|
|
| 0, 14
| 0, 08
| 0, 028
| 0, 07
| 0, 29
| 0, 014
| 0, 612
| 0, 012
| 0, 32
| 0, 45
|
|
| |
|
|
|
| 0, 15
| 0, 05
| 0.03
| 0, 072
| 0, 3
| 0, 016
| 0, 634
| 0, 014
| 0, 34
| 0, 5
|
| -5
| |
|
|
|
| 0, 16
| 0, 06
| 0, 032
| 0, 074
| 0, 31
| 0, 018
| 0, 654
| 0, 014
| 0, 38
| 0, 5
|
| -10
| |
|
|
|
| 0, 15
| 0, 06
| 0, 032
| 0, 074
| 0, 31
| 0, 018
| 0, 654
| 0, 014
| 0, 402
| 0, 53
|
| -15
| Таблица 5.2
Варианты индивидуальных заданий

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...
|

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|

Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|
Броматометрия и бромометрия Броматометрический метод основан на окислении восстановителей броматом калия в кислой среде...
Метод Фольгарда (роданометрия или тиоцианатометрия) Метод Фольгарда основан на применении в качестве осадителя титрованного раствора, содержащего роданид-ионы SCN...
Потенциометрия. Потенциометрическое определение рН растворов Потенциометрия - это электрохимический метод исследования и анализа веществ, основанный на зависимости равновесного электродного потенциала Е от активности (концентрации) определяемого вещества в исследуемом растворе...
|
Этапы трансляции и их характеристика Трансляция (от лат. translatio — перевод) — процесс синтеза белка из аминокислот на матрице информационной (матричной) РНК (иРНК...
Условия, необходимые для появления жизни История жизни и история Земли неотделимы друг от друга, так как именно в процессах развития нашей планеты как космического тела закладывались определенные физические и химические условия, необходимые для появления и развития жизни...
Метод архитекторов Этот метод является наиболее часто используемым и может применяться в трех модификациях: способ с двумя точками схода, способ с одной точкой схода, способ вертикальной плоскости и опущенного плана...
|
|

 и тангенциальных
и тангенциальных 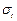 напряжений в диске молотковой дробилки; определение местного коэффициента запаса прочности;
напряжений в диске молотковой дробилки; определение местного коэффициента запаса прочности; , м/с; радиальное напряжение на поверхности посадочного отверстия диска σ r 1, МПа.
, м/с; радиальное напряжение на поверхности посадочного отверстия диска σ r 1, МПа. . (5.14)
. (5.14)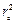 , м2
, м2  . (5.15)
. (5.15)
 . (5.16)
. (5.16) . (5.17)
. (5.17) . (5.18)
. (5.18) . (5.19)
. (5.19) . (5.20)
. (5.20) . (5.21)
. (5.21) , обусловленным центробежной силой инерции молотков и осей.
, обусловленным центробежной силой инерции молотков и осей. , (5.22)
, (5.22) . (5.23)
. (5.23) , МПа, определяется по зависимости
, МПа, определяется по зависимости ; (5.24)
; (5.24) . (5.25)
. (5.25)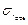 являются граничными условиями, позволяющими определить тангенциальное напряжение
являются граничными условиями, позволяющими определить тангенциальное напряжение  при r = r 1 на поверхности посадочного отверстия диска.
при r = r 1 на поверхности посадочного отверстия диска. (5.26)
(5.26) , (5.27)
, (5.27) – частота вращения ротора дробилки, об/мин.
– частота вращения ротора дробилки, об/мин. , (5.28)
, (5.28) , T – расчетные коэффициенты при r = r отв.
, T – расчетные коэффициенты при r = r отв. на N участков (рис. 5.5, а) и определим текущие значения радиуса r, м. Рекомендуемое значение N = 5.
на N участков (рис. 5.5, а) и определим текущие значения радиуса r, м. Рекомендуемое значение N = 5. (5.29)
(5.29) ; (5.30)
; (5.30) , (5.31)
, (5.31)
 – расчетные коэффициенты; определяются по вышеприведенным зависимостям (5.26) и (5.27).
– расчетные коэффициенты; определяются по вышеприведенным зависимостям (5.26) и (5.27). ; (5.32)
; (5.32) с допускаемым
с допускаемым  . В случае, если
. В случае, если  , измените исходные данные, пользуясь рекомендациями:
, измените исходные данные, пользуясь рекомендациями: не изменялась;
не изменялась;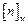 , рекомендуется увеличить ширину диска b или выбрать материал диска с большим пределом текучести.
, рекомендуется увеличить ширину диска b или выбрать материал диска с большим пределом текучести. , (5.33)
, (5.33) – соответственно массы вала, молотка, оси, диска и втулки, кг;
– соответственно массы вала, молотка, оси, диска и втулки, кг;  – количество втулок; d =2 r 1 – диаметр вала ротора, м; l вт = 0, 005 + δ – длина втулки, м; d вт =2 r 1 + 0, 012 – наружный диаметр втулки, м.
– количество втулок; d =2 r 1 – диаметр вала ротора, м; l вт = 0, 005 + δ – длина втулки, м; d вт =2 r 1 + 0, 012 – наружный диаметр втулки, м. . (5.34)
. (5.34) , (5.35)
, (5.35) . (5.36)
. (5.36) . На основании этого анализа измените исходные данные и расчет повторите.
. На основании этого анализа измените исходные данные и расчет повторите. ,
м/с
,
м/с
 , МПа
, МПа



