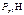Расчет виброизоляции центрифуги
Цель работы: приобретение практических навыков расчета виброизоляции центрифуги и конструирование пружинных виброизоляторов. Задание: рассчитать виброизоляцию под центрифугу (рис. 7.10), если задано: масса центрифуги m ц, кг; масса циклона m о, кг; масса привода m п, кг; частота вращения ротора ω р, с-1; динамическая нагрузка, возникающая при вращении ротора Р д, Н; масса фундамента m ф, кг; угловая частота собственных колебаний центрифуги по оси 0Z ω z = 0, 18 ω р; количество пружин n, шт; средний диаметр пружины D, м.
Методика расчета
Найдем массу всей системы, кг,
Жесткость всех виброизоляторов в вертикальном направлении, Н/м
На каждую пружину действует статическая нагрузка, Н
где g = 9, 81 м/с2 – ускорение свободного падения. Пусть пружины выполнены из стали 60С2А, для которой допускаемое напряжение при сдвиге Определяем диаметр прутка пружины
где k – коэффициент, учитывающий кривизну прутка (в предварительных расчетах k = 1, 3).
Рис. 7.10. Схема установки центрифуги на вибоизоляторах (О, А, В, С, D – центры масс соответственно системы, центрифуги, привода, основания, циклона)
Полученное по формуле (7.24) значение Жесткость одной пружины в вертикальном направлении, Н/м,
где При i < 7 число нерабочих витков рекомендуется принимать равным 1, 5 витка (на оба торца пружины); а при i > 7 – равным 2, 5. Шаг пружины, м,
Высота ненагруженной пружины, м
Осадка пружины под действием статической нагрузки, м,
Жесткость цилиндрической пружины в горизонтальном направлении, Н/м,
где Координаты центра масс системы, м (рис. 7.10)
Определим амплитуду поступательных колебаний центра масс системы по формулам, м:
Найдем частоту собственных колебаний, рад2/с2:
Динамическая нагрузка, Н, на несущую конструкцию: – вертикальная составляющая
– горизонтальная составляющая
Порядок оформления отчета. Отчет о расчетно-проектной работе включает в себя следующие разделы: – цель работы; – теоретическую часть, в которой приводятся основные положения теории о причинах возникновения вибраций, способах их устранения, методах виброзащиты и т.д.; – расчетную часть, в которой приводится расчет виброизоляции центрифуги по предлагаемому варианту (табл. 7.2); – графическую часть, содержащую чертеж пружинного виброизолятора.
Контрольные вопросы 1. Назовите причины возникновения вибраций пищевых машин. 2. Какие способы виброзащиты оборудования Вы знаете? 3. Классификация виброизоляторов. Поясните их устройство, укажите достоинства и недостатки. 4. В чем заключается сущность расчета виброизоляции? 5. Какими рекомендациями нужно руководствоваться при проектировании машин с целью уменьшения вибраций? 6. Как рассчитывается жесткость пружинных и резиновых виброизоляторов? Таблица 7.2 Варианты индивидуальных заданий
|

 (7.21)
(7.21) (7.22)
(7.22) (7.23)
(7.23)
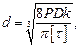 (7.24)
(7.24)
 округляем в большую сторону до ближайшего целого значения, рекомендуемого ГОСТом.
округляем в большую сторону до ближайшего целого значения, рекомендуемого ГОСТом. (7.25)
(7.25) (7.26)
(7.26) – модуль сдвига;
– модуль сдвига;  – отношение среднего диаметра D пружины к диаметру d прутка (рекомендуется c = 3, 5…8, 0).
– отношение среднего диаметра D пружины к диаметру d прутка (рекомендуется c = 3, 5…8, 0). (7.27)
(7.27)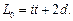 (7.28)
(7.28) (7.29)
(7.29) (7.30)
(7.30) – высота пружины в смонтированном состоянии, м; u – коэффициент, зависящий от деформации пружины (при
– высота пружины в смонтированном состоянии, м; u – коэффициент, зависящий от деформации пружины (при  коэффициент
коэффициент  ).
).
 (7.31)
(7.31)
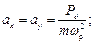 (7.32)
(7.32) (7.33)
(7.33) (7.34)
(7.34) (7.35)
(7.35) (7.36)
(7.36) (7.37)
(7.37)