Построение участка паспорта прочности горных пород
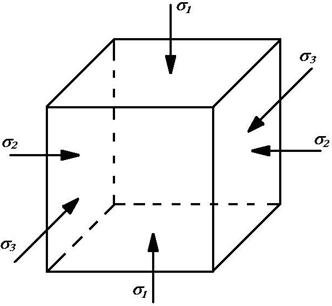
Во всех подземных горных выработках целики, кровля, почва, забой и стенки находятся в условиях всестороннего неравномерного напряженного состояния. Поэтому определение прочностных свойств горных пород в состоянии только одноосного сжатия или растяжения не всегда удовлетворяет потребностям практики. Существуют следующие классы напряженных состояний сжатия: одноосное - σ 1 ≥ 0; σ 2 = σ 3 = 0; двухосное - σ 1 = К· σ 2; σ 3 = 0; трехосное или объёмное. Известны три варианта трехосного сжатия (рис. 2.4): σ 1 = σ 2 = σ 3 ≥ 0; σ 1 ≥ σ 2 = σ 3 ≥ 0 и σ 1 ≠ σ 2 ≠ σ 3, где σ 1, σ 2, σ 3 - главные напряжения.
Рис. 2.4. Напряжения, действующие на элементарный объем породы, расположенный в породном массиве и находящийся в сложном напряженном состоянии.
Условие разрушения материала, находящегося в сложнонапряжённом состоянии, можно выразить следующей формулой:
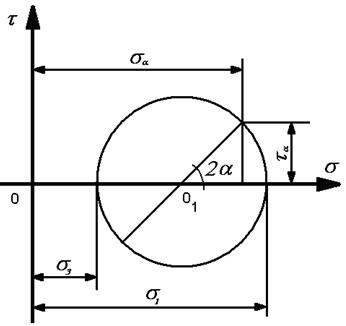
Всякое объемное напряженное состояние может быть разложено на три плоских напряженных состояния, соответствующих трем координатным плоскостям. Плоское же напряженное состояние материала может быть изображено кругом Мора, построенным на главных напряжениях s1 и s3 (максимальное и минимальное напряжения) в системе прямоугольных координат s - t (рис. 2.6). Этот способ изображения плоского напряженного состояния материала в данной точке характеризуется не только главными напряжениями s1 и s3 но и напряжениями sa и ta, действующими по произвольным площадкам, проходящим через рассматриваемую точку. Значения sa и ta определяются по формулам:
где a - угол между направлением большего по значению главного нормального напряжения s1 и нормалью к плоскости скольжения. Если напряжения s1 и s3 достигают таких величин, что вызывают предельное напряженное состояние, при котором происходит разрушение материала, то соответствующий круг будет называться предельным. Все точки, лежащие внутри круга, указывают на то, что материал может выдержать такое напряженное состояние, а точки за пределами круга свидетельствуют о том, что материал разрушился. Промежуточное sα , среднее по абсолютной величине главное напряжение, по теории Мора никакой роли не играет.
Рис. 2.6. Графическое изображение плоского напряженного состояния твердого тела
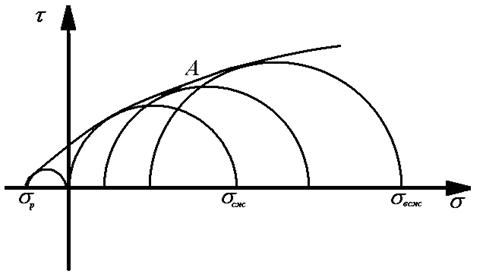
Если для нескольких разных видов напряженного состояния опытным путем получить предельные круги напряжений и нанести их на одну диаграмму, то все это семейство предельных кругов напряжений Мора имеет общую огибающую кривую линию, которая состоит из двух ветвей, располагающихся симметрично относительно оси s. Эта симметрия диктуется очевидным соображением, что при всяком нормальном напряжении равновероятны два противоположных касательных напряжения. На рис. 2.7 изображена ветвь огибающей кривой линии к предельным кругам Мора, причем первые два круга соответствуют одноосному растяжению и одноосному сжатию.
Рис. 2.7. Характер огибающих наибольших кругов напряжений Мора для одноосного растяжения sр, одноосного сжатия sсж, всестороннего неравномерного сжатия sвсж
Можно построить как угодно много кругов напряженных состояний. Огибающую кривую линию предельных кругов напряжений называют паспортом прочности горной породы, поскольку она характеризует условие разрушения породы, находящейся в сложном напряженном состоянии. Очевидно, что любое напряженное состояние породы, характеризуемое точкой, лежащей выше огибающей предельных кругов Мора, является разрушающим для данной породы. Значение t в любой точке паспорта прочности может быть определено (например, в точке А) по формуле: Как видно из рисунка 2.7., угол внутреннего трения для горных пород, находящихся в сложном напряженном состоянии, не является величиной постоянной, а является некоторой функцией нормального напряжения: Оборудование и материалы: гидравлический пресс, штангенциркуль, образцы испытываемой породы стандартных размеров (d = h = 40 ¸ 45мм). Порядок проведения эксперимента. Подготавливают к работе пресс. Определяют площадь поперечного сечения образцов. По методике работы 2.1. вычисляют предел прочности породы на одноосное сжатие. Опыт повторяют на 3-5 образцах. Также на 3-5 образцах определяют предел прочности горной породы на растяжение с использованием косвенного метода - раскалывание цилиндрических образцов (по методике работы 2.3.). Предел прочности породы на одноосное сжатие рассчитывают по формуле: sсж=4F/( По найденным средним значениям (sсж) и (sр) строят в координатах (s- t) предельные круги Мора (рис. 2.8) и проводят к ним касательную линию. Графически или аналитически определяют значение угла внутреннего трения j и силу сцепления С. Результаты эксперимента заносятся в таблицу замеров (форма 10).
|

 Применительно к горным породам, находящимся в условиях сложного напряженного состояния, для оценки этого состояния наибольшее распространение получила теория прочности Мора. Согласно этой теории, разрушение материала происходит не отдельно от нормальных (s) или касательных (t)напряжений, а от некоторой их комбинации. Для каждого вида сложного напряженного состояния характерна своя функция t = f (s) зависимости между касательными и нормальными напряжениями на площадке разрушения. Сопротивление разрушению материала слагается из силы сцепления (С) и силы внутреннего трения (F), значение которой определяется по формуле:
Применительно к горным породам, находящимся в условиях сложного напряженного состояния, для оценки этого состояния наибольшее распространение получила теория прочности Мора. Согласно этой теории, разрушение материала происходит не отдельно от нормальных (s) или касательных (t)напряжений, а от некоторой их комбинации. Для каждого вида сложного напряженного состояния характерна своя функция t = f (s) зависимости между касательными и нормальными напряжениями на площадке разрушения. Сопротивление разрушению материала слагается из силы сцепления (С) и силы внутреннего трения (F), значение которой определяется по формуле:  где, y - коэффициент трения; N - величина нормального давления.
где, y - коэффициент трения; N - величина нормального давления.
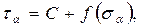 где, ta, sa - компоненты напряжения на площадке скольжения (рис. 2.5).
где, ta, sa - компоненты напряжения на площадке скольжения (рис. 2.5).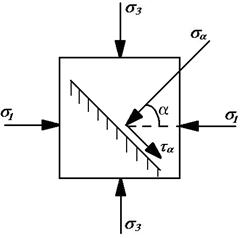 Рис. 2.5. Схема определения ta и sa по наклонным площадкам при плоском напряженном состоянии.
Рис. 2.5. Схема определения ta и sa по наклонным площадкам при плоском напряженном состоянии.
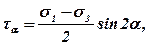
 где jа - угол внутреннего трения, tgjа - коэффициент внутреннего трения породы.
где jа - угол внутреннего трения, tgjа - коэффициент внутреннего трения породы.
 ·d2). Полученные значения (sсж) усредняют. Предел прочности исследуемой породы на растяжение рассчитывается по формуле: sр= 2Fmax./(
·d2). Полученные значения (sсж) усредняют. Предел прочности исследуемой породы на растяжение рассчитывается по формуле: sр= 2Fmax./(


