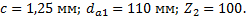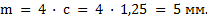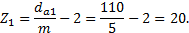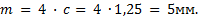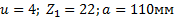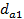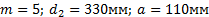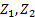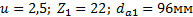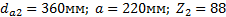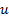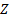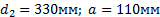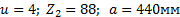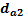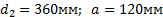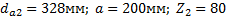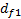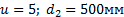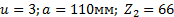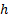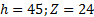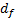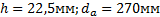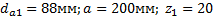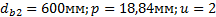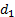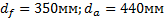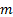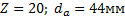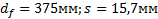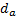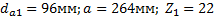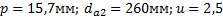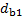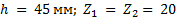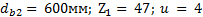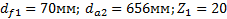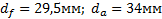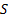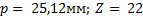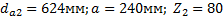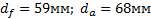Решение для простой зубчатой передачи
1.Передача имеет четыре ступени:
2, Угловая скорость ведущего зубчатого колеса Z1 находится по формуле (2.4):
3. Угловая скорость ведомого зубчатого колеса
Знак " минус" показывает, что угловая скорость ведомого зубчатого колеса 4. Частота вращения ведомого зубчатого колеса
Решение для сложной зубчатой передачи 1. Заданная передача состоит из одноступенчатой простой зубчатой передачи, содержащей колеса 2. Для простой зубчатой передачи передаточное отношение находим через числа зубьев колес по формуле (2.3).
3. Для планетарной зубчатой передачи передаточное отношение находим, пользуясь зависимостью (3.2).
где Схема обращенного механизма для этой планетарной зубчатой передачи показана на рис: 2.8, б. Передаточное отношение обращенного механизма:
Подставляя полученное выражение в предыдущую формулу, получаем
При передаче движения в данной планетарной передаче ведущим звеном является водило Н, а ведомым звеном - колесо
4. Общее передаточное отношение заданной сложной зубчатой передачи находим как произведение передаточных отношений простой и планетарной зубчатых передач.
По абсолютной величине передаточное отношение меньше единицы. Это означает, что заданная передача является мультипликатором, а не редуктором. Эта передача предназначена для увеличения частоты вращения, а не для уменьшения. 5. Угловая скорость ведущего зубчатого колеса
6. Угловая скорость ведомого зубчатого колеса
Знак " минус" показывает, что угловая скорость
Рис. 2.8. Схемы: а) заданной сложной зубчатой передачи; б) обращенного механизма для планетарной зубчатой передачи 7. Частота вращения ведомого зубчатого колеса находится
2.6. Вопросы для проверки знаний 1. Что называют механическими передачами? 2. Какая зубчатая передача называется простой? 3. Что называют ступенью простой зубчатой передачи? 4. Что называют передаточным отношением? 5. Какой вид имеет схема одноступенчатой простой цилиндрической зубчатой прямозубой передачи внешнего зацепления? 6. Какой вид имеет схема одноступенчатой простой цилиндрической зубчатой прямозубой передачи внутреннего зацепления? 7. Какой знак имеет передаточное отношение одноступенчатой простой цилиндрической зубчатой передачи внешнего зацепления? Какой знак имеет передаточное отношение одноступенчатой простой цилиндрической зубчатой передачи внутреннего зацепления? 8. Какой знак имеет передаточное отношение одноступенчатой простой цилиндрической зубчатой передачи внутреннего зацепления? 9. Как выражается передаточное отношение одноступенчатой зубчатой передачи через угловые скорости колес? 10. Как выражается передаточное отношение одноступенчатой зубчатой передачи через числа зубьев колес? 11. Какие зубчатые передачи называют редукторами? 12. Какие зубчатые передачи называют мультипликаторами? 13. Почему в машинах обычно применяют редукторы? 14. В каких устройствах применяются мультипликаторы? 15. Как определить общее передаточное отношение многоступенчатой простой цилиндрической зубчатой передачи? 16. Что означает положительный знак общего передаточного отношения многоступенчатой простой цилиндрической зубчатой передачи? 17. Что означает отрицательный знак общего передаточного отношения многоступенчатой простой цилиндрической зубчатой передачи? 18. Какие Вы можете привести примеры использования зубчатых простых передач в машинах? 19. Какие Вы можете привести примеры использования зубчатых простых передач в приборах? 20. Как называют зубчатые простые передачи, у которых можно изменять передаточное отношение? 21. Каким образом в машинах выполняют изменение передаточного отношения простых зубчатых передач? 22. У редукторов передаточное отношение по абсолютной величине больше или меньше единицы? 23. У мультипликаторов передаточное отношение по абсолютной величине больше или меньше единицы? 24. Какие зубчатые передачи называются цилиндрическими? 25. Какие зубчатые передачи называются прямозубыми? 26. Какие зубчатые передачи называют сложными? 27. Какие названия имеют сложные зубчатые передачи? 28. Из каких звеньев состоят планетарные зубчатые передачи? 29. Какое звено планетарной зубчатой передачи называют сателлитом? 30. Какое звено планетарной зубчатой передачи называют водилом? 31. Какое звено планетарной зубчатой передачи называют солнечным зубчатым колесом? 32. Какое звено планетарной зубчатой передачи называют опорным зубчатым колесом? 33. В чем состоит метод обращенного движения, применяемый для исследования передачи движения в планетарных зубчатых передачах? 34. Чем отличается обращенный механизм от планетарной зубчатой передачи? 35. Как определяется общее передаточное отношение обращенного зубчатого механизма? 36. По какой формуле вычисляют общее передаточное отношение планетарной зубчатой передачи? 37. Как определить общее передаточное отношение механизма, состоящего из последовательно соединенной простой зубчатой передачи и планетарной зубчатой передачи? 38. Как определить общее передаточное отношение механизма, состоящего из последовательно соединенных планетарных зубчатых передач? 39. Чем отличается планетарный зубчатый механизм от дифференциального зубчатого механизма? 40. Какие звенья планетарного зубчатого механизма называются центральными? 41. Какие достоинства имеют планетарные зубчатые передачи по сравнению с простыми зубчатыми передачами? 42. Какие Вы знаете примеры применения планетарных зубчатых передач в машинах? 43. Чем отличаются планетарные зубчатые передачи - редукторы от планетарных зубчатых передач - мультипликаторов?
3. СИНТЕЗ ПЛАНЕТАРНОЙ ЗУБЧАТОЙ ПЕРЕДАЧИ
3.1. Условия синтеза планетарных зубчатых передач Задача синтеза механизма - это задача его проектирования, задача определения параметров механизма. В данном разделе рассматривается задача геометрического синтеза планетарных зубчатых передач с одновенцовым сателлитом, схемы которых показаны на рис. 3.1, по заданному значению передаточного отношения этой передачи. При решении задачи находят числа зубьев зубчатых колес Z1, Z2 и Z3, количество сателлитов К и радиусы делительных окружностей зубчатых колес r1, г2 и r3. Проектируем передачу с нулевыми зубчатыми колесами. При этом требуется выполнить условия проектирования планетарной зубчатой передачи. Условие 1 (условие отсутствия подрезания или заклинивания зубьев колес). Для выполнения этого условия принятое число зубьев Zi любого колеса должно быть не менее 17 зубьев:
Условие 2 (кинематическое условие) состоит в следующем: числа зубьев колес должны быть такими, при которых передаточное отношение планетарной зубчатой передачи равно заданному значению. С учетом сведений, изложенных в разделе 3.2, выведем аналитически это условие для каждого из четырех типов планетарных зубчатых механизмов, показанных на рис. 3.1. Тип 1:
Отсюда
Тип 2:
Отсюда
Тип 3:
Отсюда
Тип 4:
Отсюда
Условие 3 (условие соосности центральных зубчатых колес) Обозначим межосевые расстояния: а12 - для зацепления зубчатых колес Z1 и Z2; а23 - для зацепления зубчатых колес Z2 и Z3. Должно выполняться условие а12 = а23, или r1+r2=r3-r2. Пусть m- модуль всех зубчатых колес передачи. Тогда
Условие 4 (условие соседства сателлитов) В планетарных зубчатых передачах для уменьшения нагрузок на зубья колес и обеспечения динамической уравновешенности механизма на водиле обычно устанавливают не один, а несколько одинаковых сателлитов, расположенных в одной плоскости равномерно. Принятое количество " К" сателлитов должно быть таким, при котором окружности выступов сателлитов не пересекаются. Для механизмов, представленных на рис. 3.1, условие соседства сателлитов имеет вид
Условие 5 (условие сборки планетарной зубчатой передачи) Для того чтобы при принятых значениях чисел зубьев колес и количестве сателлитов " К" была возможна сборка планетарных зубчатых передач, показанных на рис. 3.1, необходимо выполнение условия
где γ - целое и положительное число.
3.2. Задание на практическое занятие № 3
Выполнить геометрический синтез планетарной зубчатой передачи с одновенцовым сателлитом. Схема заданной передачи приведена на рис. 3.1. Тип передачи, общее передаточное отношение передачи и модуль зубчатых колес даны в табл. 3.1. Вариант исходных данных студенту задает преподаватель. Необходимо определить числа зубьев и диаметры делительных окружностей всех зубчатых колес передачи, назна чить количество сателлитов.
3.3. Последовательность выполнения задания № 3 Изобразить кинематическую схему планетарной зубчатой передачи заданного типа и переписать заданные исходные данные, переписать задание на практическое занятие №3. После этого выполнять синтез передачи в следующем порядке 1. Для выполнения условия отсутствия подрезания или заклинивания зубьев колес (3.1) и уменьшения габаритов передачи принять число зубьев Z1= 17. 2. Найти число зубьев Z3, используя кинематическое условие (3.2), (3.3), (3.4) или (3.5), которое соответствует заданному типу планетарной зубчатой передачи. Полученное значение Z3 округлить до целого числа. Разность (Z3-Z1) должна быть четным числом для того, чтобы при дальнейшем расчете число зубьев Z2 получилось целым. 3. Из условия соосности (3.6) найти число зубьев Z2 сателлита. Если получится Z2< 17, то, последовательно увеличивая Z1 на единицу (принимая Z1= 18, 19, 20,....), необходимо вновь выполнять расчет чисел зубьев колес, начиная с п.2, до тех пор, пока не будет выполнено условие (3.1). 4. Принять количество сателлитов К=3. Проверить выполнение условия соседства сателлитов (3.7). Если это условие не выполняется принять количество сателлитов К=2. Условие соседства сателлитов при этом будет выполняться.
5. Проверить выполнение условия сборки (3.8) планетарной зубчатой передачи. Если условие сборки не выполняется, то принять количество сателлитов К=2. Условие сборки при этом будет выполняться. 6. Вычислить диаметры делительных окружностей всех зубчатых колес передачи по формуле d= т· Z. 3.4. Пример выполнения задания № 3 Задание. Выполнить геометрический синтез планетарной зубчатой передачи с одновенцовым сателлитом. Схема заданной передачи дана на рис. 3.1. Исходные данные: тип передачи 4, общее передаточное отношение передачи Необходимо определить числа зубьев и диаметры делительных окружностей всех зубчатых колес передачи, назначить количество сателлитов. Решение: 1. Проектируем передачу из нулевых зубчатых колес. Для выполнения условия (3.1) отсутствия подрезания или заклинивания зубьев принимаем число зубьев Z1= 17. 2. Из кинематического условия (3.5) для планетарной зубчатой передачи типа 4 на рис.3.1 находим число зубьев Z3.
Округляем полученное число зубьев до целого числа так, чтобы разность (Z3 -Z1) была четным числом. Принимаем Z3= 59. При этом получаем Z3- Z1= 59 -17 = 42 - четное число. 3. Из условия соосности (3.6) находим число зубьев Z2 сателлита.
4. Принимаем количество сателлитов К=3. Проверяем выполнение условия соседства сателлитов (3.7).
5. Проверяем выполнение условия сборки (3.8) планетарной зубчатой передачи.
Так как полученное значение γ = 25, 33 не является целым числом, то условие сборки не выполняется. Поэтому принимаем количество сателлитов К=2. Вновь проверяем выполнение условия сборки передачи.
Условие сборки выполнено. Окончательно принято К=2. 6. Вычисляем диаметры делительных окружностей всех зубчатых колес передачи:
3.5. Вопросы для проверки знаний 1. Чем отличается задача синтеза механизма от задачи анализа механизма? 2. Что задано и что определяют при решении задачи геометрического синтеза планетарной зубчатой передачи? 3. Какие условия требуется выполнить при решении задачи геометрического синтеза планетарной зубчатой передачи? 4. Как обеспечивается выполнение условия отсутствия подрезания зубьев колес при синтезе планетарной зубчатой передачи? 5. В чем состоит кинематическое условие синтеза планетарной зубчатой передачи? 6. В чем состоит условие соосности для планетарных зубчатых передач? 7. Для чего необходимо при синтезе планетарных зубчатых передач выполнение условия соседства сателлитов? 8. Почему при синтезе планетарных зубчатых передач требуется выполнить условие сборки? 9. Какие параметры планетарной зубчатой передачи находят при использовании кинематического условия и условия соосности во время синтеза этой передачи? 10. Какой параметр планетарной зубчатой передачи находят при использовании условия соседства сателлитов и условия сборки во время синтеза этой передачи? 11. Что необходимо предпринять при синтезе планетарной зубчатой передачи в случае невыполнения условия соседства сателлитов? 12. Что необходимо предпринять при синтезе планетарной зубчатой передачи в случае невыполнения условия ее сборки? 13. Почему проектируют планетарные зубчатые передачи, принимая число сателлитов больше единицы?
4. ОПРЕДЕЛЕНИЕ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ НУЛЕВОЙ ЦИЛИНДРИЧЕСКОЙ ПРЯМОЗУБОЙ ЭВОЛЬВЕНТНОЙ ПЕРЕДАЧИ 4.1. Основные сведения о геометрических параметрах нулевых цилиндрических прямозубых эвольвентных передач Зубчатые передачи - механизмы, в которых вращательное движение между звеньями (зубчатыми колесами) передается с помощью последовательно зацепляющихся зубьев (рис. 4.1). Цилиндрическими называются зубчатые передачи с параллельным расположением осей сопряженных зубчатых колес. Прямозубыми называются зубчатые передачи, имеющие прямые линии в качестве образующих боковых поверхностей зубьев колес. Профиль зуба цилиндрического прямозубого колеса - это линия пересечения боковой поверхности зуба с плоскостью, перпендикулярной оси колеса. Эвольвентная зубчатая передача - это передача, у которой профили зубьев колес очерчены эвольвентами окружностей. Эвольвента окружности - плоская кривая, описываемая точкой прямой линии, перекатываемой по окружности без скольжения.
Основная окружность - окружность зубчатого колеса, по которой перекатывается прямая при образовании эвольвенты профиля зуба колеса. Построение эвольвенты показано на рис. 4.2.
Нулевое зубчатое колесо - зубчатое колесо, при нарезании зубьев которого отсутствовало (было равно нулю) смещение зуборезного инструмента по отношению к заготовке колеса. Делительная окружность зубчатого колеса - окружность, которая в процессе нарезания зубьев колеса перекатывается без скольжения по делительной прямой или делительной окружности зуборезного инструмента. Начальная окружность зубчатого колеса - окружность, которая при работе зубчатой передачи перекатывается без скольжения по начальной окружности сопряженного зубчатого колеса. Точка касания начальных окружностей называется полюсом зацепления Π (рис.4.3). У нулевых зубчатых колес делительная и начальная окружности совпадают. Зубья ограничены по высоте окружностями выступов (вершин) и окружностями впадин. Полная (общая) высота зуба «h» - радиальное расстояние между окружностями выступов и впадин зубчатого колеса.
Рис. 4.3. Зацепление эвольвентной прямозубой цилиндрической передачи с нулевыми колесами Полная высота зуба складывается из высоты головки и высоты ножки зуба. Высота головки зуба “h а ” радиальное расстояние между окружностью выступов (вершин) и начальной окружностью. Высота ножки зуба " Межосевое расстояние а = аw - расстояние между осями колес нулевой цилиндрической зубчатой передачи. Обозначения диаметров окружностей зубчатых колес: da1, da2 - диаметры окружностей выступов; df1, df2 - диаметры окружностей впадин; dw1, dw2 - диаметры начальных окружностей; d1, d2 - диаметры делительных окружностей; db1, db2 - диаметры основных окружностей. Радиальный зазор ”с” - расстояние между окружностями выступов и впадин сопряженных колес, измеренное на межосевой линии. Этот зазор имеет место в двух местах (рис. 4.3) и он одинаковый. На рис 4.3 показан также боковой зазор “δ ” между зубьями колес. У теоретически точно изготовленной передачи в положении зубьев, показанном на рис. 4.3, этого зазора быть не должно. Он возникает лишь от погрешностей при изготовлении и сборке колес, а также ввиду изнашивания боковых поверхностей зубьев при работе передачи. Различают внешние и внутренние зубья. У внешних зубьев окружность выступов находится снаружи окружности впадин; у внутренних - внутри окружности впадин (рис. 4.4). Каждый зуб очерчен двумя симметрично расположенными профилями. Расстояние между этими профилями, измеренное по делительной окружности, называют толщиной зуба и обозначают “s”. У нулевых колес толщина зуба равна ширине впадины между зубьями по делительной окружности. Толщина зубьев сопряженных нулевых колес по делительным окружностям одинакова: S = S1 = S2.
Рис. 4.4. Форма зубьев зубчатых колес: а) внешних; б) внутренних Шаг зубчатого колеса " р" - расстояние между двумя одинаково расположенными точками двух соседних зубьев, измеренное по окружности.Измерение шага выполняют по делительной окружности. Зубчатые колеса, входящие в зацепление, имеют одинаковый шаг и одинаковый модуль. Модуль " m" - это отношение шага к числу π:
Модуль " m" - это часть диаметра делительной окружности зубчатого колеса, приходящаяся на один зуб:
Модуль - основной параметр зубчатой передачи. Через модуль выражают все остальные геометрические параметры ее. Модуль выражается в миллиметрах. Значения модуля стандартизированы. В первом, предпочтительном, ряду значений модуля, предусмотрены следующие модули в мм: 0; 0, 05; 0, 06; 0, 08; 0, 1; 0, 12; 0, 15; 0, 2; 0, 25; 0, 3; 0, 4; 0, 5; 0, 8; 1, 0; 1, 25; 1, 5; 2; 2, 5; 3; 4; 5; 6; 8; 10; 12; 15; 20; 25; 32; 40; 50; 60; 80; 100. Во втором ряду предусмотрены модули, промежуточные между модулями первого ряда, например: 0, 9; 1, 125; 1, 375; 1, 75; 2, 25; 2, 75; 3, 5; 4, 5; 5, 5; 7.
Делительную окружность можно определить как окружность, для которой модуль имеет стандартную величину, или как окружность, которая является базовой для определения размеров зубьев. Через модуль параметры нулевой цилиндрической эвольвентной прямозубой передачи выражаются следующим образом:
В технике используются также зубчатые передачи с внутренним зацеплением зубьев колес (рис. 4.5). Внутреннее зацепление по сравнению с внешним зацеплением из-за сложности изготовления передачи менее распространено. Оно применяется обычно в планетарных передачах, механизмах поворота платформы машины и других случаях. Для зубчатой передачи с внутренним зацеплением зубьев:
Рис. 4.5. Прямозубая цилиндрическая передача с внутренним зацеплением зубьев: а) внешний вид; б) схема
4.2. Задание на практическое занятие № 4 Определить требуемые параметры нулевой цилиндрической прямозубой эвольвентной передачи. Вид зацепления зубчатых колес (внешнее или внутреннее) и заданные величины параметров рассматриваемой передачи приведены в табл. 5.1. Вариант исходных данных студенту задает преподаватель.
4.3. Последовательность выполнения задания №4 Переписать из табл. 4.1 заданные исходные данные и переписать задание на практическое занятие № 4. После этого выполнять определение геометрических параметров зубчатой передачи, используя зависимости (4.1) - (4.18). Очередность определения параметров заданной зубчатой передачи определять самостоятельно.
4.4. Пример выполнения задания № 4
Задание. Выполнить определение геометрических параметров нулевой цилиндрической прямозубой эвольвентной передачи. Вид зацепления зубчатых колес - внешнее. Заданные величины:
Определить межосевое расстояние зубчатой передачи а. Решение: 1. Из формулы (4.16) по заданному значению радиального зазора с вычисляем модуль зубчатых колес:
2. Определяем число зубьев
3, Определяем межосевое расстояние а зубчатой передачи по формуле (4.17):
Возможна иная последовательность решения задания. 1. Из формулы (4.16) по заданному значению радиального зазора " с" вычисляем модуль зубчатых колес:
2. Определяем диаметр окружности впадин зубчатого колеса по формуле (4.9):
|

 . Из них три ступени внешнего зацепления и одна ступень
. Из них три ступени внешнего зацепления и одна ступень 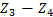 - внутреннего зацепления. Общее передаточное отношение передачи находим как произведение передаточных отношений четырех ступеней. Передаточные отношения отдельных ступеней выражаем через числа зубьев зубчатых колес с учетом зависимостей (2.1) и (2.2).
- внутреннего зацепления. Общее передаточное отношение передачи находим как произведение передаточных отношений четырех ступеней. Передаточные отношения отдельных ступеней выражаем через числа зубьев зубчатых колес с учетом зависимостей (2.1) и (2.2).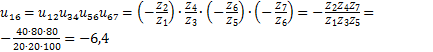 .
.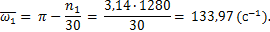
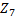 находится по формуле(2.3):
находится по формуле(2.3):
 . На схеме механизма (рис.2.7) показываем направление
. На схеме механизма (рис.2.7) показываем направление 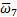 пунктирной линией.
пунктирной линией.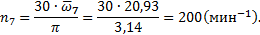
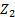 , и последовательно соединенной с ней, планетарной зубчатой передачи, содержащей водило Н, сателлит
, и последовательно соединенной с ней, планетарной зубчатой передачи, содержащей водило Н, сателлит 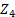 , корончатое
, корончатое 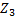 и солнечное
и солнечное  зубчатые колеса.
зубчатые колеса.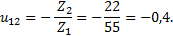
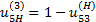
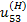 - передаточное отношение обращенного механизма.
- передаточное отношение обращенного механизма.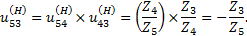
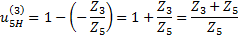
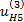 :
: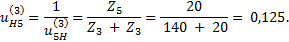
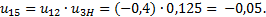
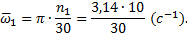
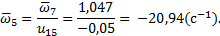
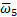 ведомого зубчатого колеса
ведомого зубчатого колеса  , ведущего зубчатого колеса
, ведущего зубчатого колеса 
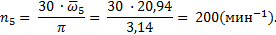
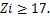 (3.1)
(3.1)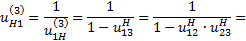
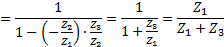
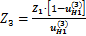 (3.2)
(3.2)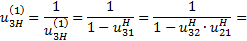

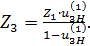 (3.3)
(3.3)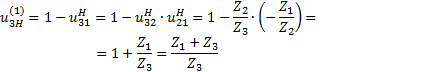
 (3.4)
(3.4)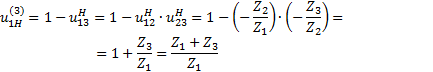
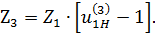 (3.5)
(3.5)
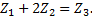
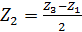 (3.6)
(3.6)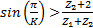 (3.7)
(3.7)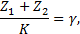 (3.8)
(3.8)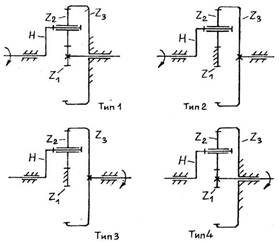 Рис. 3.1. Схемы заданных планетарных зубчатых передач с одновенцовым сателлитом
Рис. 3.1. Схемы заданных планетарных зубчатых передач с одновенцовым сателлитом

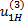

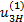
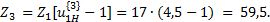
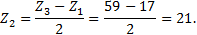
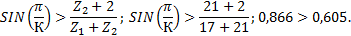

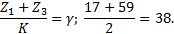
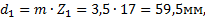
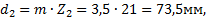
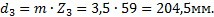
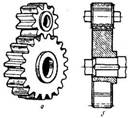 Рис. 4.1. Прямозубая цилиндрическая зубчатая передача с внешним зацеплением зубьев:
а) внешний вид; б) эскиз
Рис. 4.1. Прямозубая цилиндрическая зубчатая передача с внешним зацеплением зубьев:
а) внешний вид; б) эскиз
 Рис. 4.2. Построение эвольвенты
Рис. 4.2. Построение эвольвенты

 " - радиальное расстояние между начальной окружностью и окружностью впадин.
" - радиальное расстояние между начальной окружностью и окружностью впадин.
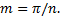 (4.1)
(4.1)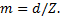 (4.2)
(4.2)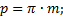 (4.3)
(4.3)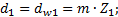 (4.4)
(4.4)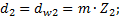 (4.5)
(4.5) (4.6)
(4.6)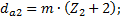 (4.7)
(4.7)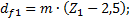 (4.8)
(4.8)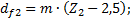 (4.9)
(4.9) (4.10)
(4.10)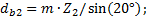 (4.11)
(4.11)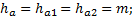 (4.12)
(4.12)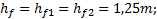 (4.13)
(4.13)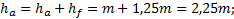 (4.14)
(4.14)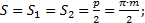 (4.15)
(4.15) (4.16)
(4.16)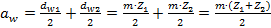 (4.17)
(4.17)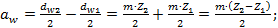 (4.18)
(4.18) (4.19)
(4.19)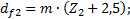 (4.20)
(4.20)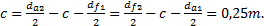 (4.21)
(4.21)