Заданы при силовом расчете обычно силы движущие или силы полезных сопротивлений, а также силы тяжести (или массы)звеньев
Последовательность силового расчета механизма сводится к: а) определению сил и моментов сил инерции, действующих на звенья; б) определению реакций в кинематических парах; в) определению так называемых уравновешивающих сил или уравновешивающих моментов. Предварительно механизм расчленяют на структурные группы звеньев и входные звенья. Структурной группой звеньев называют такую совокупность звеньев, соединенных в кинематические пары, которая после присоединения ее крайних элементов кинематических пар к стойке имеет по формуле (2.1) степень подвижности равную нулю: Если рассматриваемый механизм не имеет высших кинематических пар, то эта формула для структурных групп имеет вид
где W - степень подвижности механизма; n - количество подвижных звеньев; Из этой формулы следует, что наиболее простые структурные группы звеньев содержат два звена и три низшие кинематические пары (вращательные или поступательные). При силовом расчете механизма последовательно выполняют силовой расчет структурных групп звеньев, начиная с наиболее удаленной от входного звена структурной группы и идя в направлении к входному звену. Силовой расчет заканчивают рассмотрением входного звена. По заданию необходимо выполнить силовой расчет лишь одной простейшей структурной группы звеньев (диады), состоящей из двух звеньев и трех кинематических пар. Для этого структурную группу от механизма отделяют и изображают в рассматриваемое мгновение отдельно от кинематической схемы в масштабе длин. К звеньям в соответствующие точки прикладывают все действующие внешние силы: заданные движущие силы или силы полезных сопротивлений, силы тяжести, предварительно найденные силы инерции и моменты сил инерции. В двух крайних кинематических парах структурной группы звеньев показывают векторы внутренних сил — сил реакций, действующих от оторванных звеньев механизма на рассматриваемые звенья структурной группы. В крайней поступательной кинематической паре реакцию необходимо направлять перпендикулярно направляющей относительного поступательного движения звеньев в этой паре. Во вращательной кинематической паре обычно реакцию разлагают на две составляющие: нормальную, которая действует вдоль звена, и тангенциальную, которая действует перпендикулярно звену. Векторы всех сил на схеме структурной группы изображают не в масштабе. Так как реакции неизвестны, то направления стрелок векторов реакций и составляющих реакций показывают произвольно и при дальнейшем расчете уточняются. Звенья структурной группы считаются находящимися в равновесии, неизвестные реакции в кинематических парах находят аналитическим или графическим путем, составляя уравнения статики. Последовательность силового расчета структурной группы звеньев зависит от варианта сочетания вращательных и поступательных кинематических пар в этой группе. Рассмотрим последовательность силового расчета для различных видов структурных групп звеньев, изображенных на рис. 8.1. На схемах структурных групп показаны лишь силы или составляющие сил реакций в крайних кинематических парах. Структурная группа звеньев с тремя вращательными кинематическими парами (рис. 8.1, а): 1. Сумма всех моментов сил, действующих относительно центра средней кинематической пары В на звено 2, приравнивается нулю: 2. Сумма всех моментов сил, действующих относительно центра средней кинематической пары В на звено 3, приравнивается нулю: 3. Векторная сумма всех сил, действующих на звенья 2 и 3, приравнивается нулю: 4. Векторная сумма всех сил, действующих на звено 2, приравнивается нулю: Структурная группа звеньев с крайней поступательной и двумя вращательными кинематическими парами (рис. 8.1, б): 1. Сумма всех моментов сил, действующих относительно центра средней кинематической пары С на звено 2, приравнивается нулю: 2. Векторная сумма всех сил, действующих на звенья 2и 3, приравнивается нулю: 3. Векторная сумма всех сил, действующих на звено 3, приравнивается нулю: 4. Сумма всех моментов сил, действующих относительно центра средней кинематической пары С на звено 3, приравнивается нулю: Структурная группа звеньев с крайними вращательными и средней поступательной кинематическими парами (рис. 8.1, в): 1. Сумма всех моментов сил, действующих относительно точки А на звено 3, приравнивается нулю: 2. Вычисляется тангенциальная составляющая реакции во вращательной паре 3. Векторная сумма всех сил, действующих на звено 2, приравнивается нулю: 4. Сумма всех моментов сил, действующих относительно центра вращательной кинематической пары А на звено 2, приравнивается нулю: Структурная группа звеньев с крайней вращательной и двумя поступательными кинематическими парами (рис. 8.1, г): 1. Векторная сумма всех сил, действующих на звено 3, приравнивается нулю: 2. Векторная сумма всех сил, действующих на звено 2, приравнивается нулю:
3. Сумма всех моментов сил, действующих относительно центра вращательной кинематической пары А на звено 2, приравнивается нулю: 4. Сумма всех моментов сил, действующих относительно центра вращательной кинематической пары А на звенья 2 и 3, приравнивается нулю: Силовой расчет входного звена состоит в определении силы реакции в кинематической паре А соединения входного звена со стойкой. Для этого в масштабе длин изображают отдельно входное звено 1 со стойкой и прилагают к нему силу тяжести и силу реакции от оторванного подвижного звена механизма. Векторная сумма всех сил, действующих на входное звено 1, приравнивается нулю: Проверку силового расчета механизма по теореме Н.Е. Жуковского в данной работе не рассматриваем. 8.2. Задание на практическое занятие № 8
Выполнить силовой расчет плоского четырехзвенного механизма, для которого по заданию 6 строился план скоростей, а по заданию 7 строился план ускорений. Считать центры тяжести рычагов расположенными посредине их длины, а центры тяжести ползунов расположенными в их центре. Центр тяжести входного звена считать расположенным на оси его вращения относительно стойки. Принять массы ползунов равными 5кг, а массы рычагов - 3 кг. Масса входного звена - 5 кг. Моменты инерции рычагов вычислять по формуле
где Считать: 1) если выходное звено движется поступательно, то на него действует сила полезного сопротивления 8.3. Последовательность выполнения задания № 8
Изобразить построенный по заданию 7 план ускорений для четырехзвенного плоского механизма. Найти на плане ускорения центров тяжести звеньев. Построить в масштабе длин схему структурной группы звеньев заданного механизма. Вычислить величины сил тяжести, сил инерции и моментов сил инерции звеньев этой группы. Показать на схеме звеньев структурной группы все действующие силы и моменты сил. В соответствии с видом структурной группы звеньев определить реакции во всех трех кинематических парах этой группы. Определить силу реакции во вращательной кинематической паре соединения входного звена 1 со стойкой. Порядок действий изложен в разделе 8.1.
8.4. Пример выполнения задания № 8
Задание: Выполнить силовой расчет четырехзвенного кривошип- но-ползунного механизма, для которого по заданию 6 строился план скоростей (рис. 6.5), а по заданию 7 - план ускорений (рис. 6.6). Схема заданного механизма в масштабе длин Считаем центр тяжести входного звена - кривошипа 1 расположенным на оси его вращения А, центр тяжести S2 шатуна 2 расположенным посредине его длины ВС, а центр тяжести S3 ползуна 3 расположенным в его центре, то есть в точке С. Даны массы кривошипа 1, шатуна 2 и ползуна 3: Дана сила полезного сопротивления, действующая на выходное звено механизма - ползун 3 и препятствующая его движению: Решение: Изображаем (рис. 8.2) построенный по заданию 7 план ускорений рассматриваемого механизма. На нем, используя теорему подобия для планов ускорений, находим ускорения центров тяжести шатуна 2 и ползуна 3. Точкиs 1, s2 и s3 на плане ускорений располагаем аналогично расположению точек S1, S2 и S3 по заданию на схеме механизма: точка S1 совпадает с точкой А, точка S2 расположена посредине звена ВС, а точка S3 - совпадает с точкой С ползуна. Ускорения центров тяжести звеньев:
Строим в масштабе длин схему структурной группы звеньев 2-3 заданного механизма (рис. 8.3). Угловое ускорение ε 2 шатуна 2:
Для определения направления ε 2 проводим на схеме структурной группы звеньев 2-3 (рис. 8.3) пунктирной линией из точки С вектор ускорения Вычисляем величины сил тяжести звеньев 1, 2 и 3 по формуле (8.1):
Момент инерции шатуна 2 вычисляем по формуле (8.4):
где
Вычисляем силы инерции и моменты сил инерции звеньев этой группы по формулам (8.2) и (8.3):
Сила полезных сопротивлений Показываем на схеме структурной группы звеньев 2-3 (рис. 8.3) все действующие силы и моменты сил. Структурная группа звеньев рассматриваемого механизма имеет два звена и три кинематические пары: одну крайнюю поступательную (Д) и две вращательные (В и С). Последовательность силового расчета этой группы такая же, как для аналогичной структурной группы звеньев, показанной на рис. 8.1, 6: 1. Сумма всех моментов сил, действующих относительно центра средней кинематической пары С на звено 2, приравнивается нулю:
2. Векторная сумма всех сил, действующих на звенья 2 и 3, приравнивается нулю:
В соответствии с уравнением в масштабе сил строится план сил (рис. 8.4), на котором находят нормальную составляющую реакции и полную реакцию в крайней вращательной кинематической паре А и реакцию в поступательной паре Д:
3. Векторная сумма всех сил, действующих на звено 3, приравнивается нулю:
В соответствии с уравнением в масштабе сил строится план сил, на котором находят реакцию в средней кинематической паре Вектор реакции (рис. 8.4) цепочку известных векторов сил. Измеряем длину этого вектора и находим его величину:
4. Сумма всех моментов сил, действующих относительно центра средней кинематической пары С на звено 3, приравнивается нулю: Силовой расчет входного звена состоит в определении силы реакции в кинематической паре А соединения входного звена 1 со стойкой 4. Для этого в масштабе длин изображаем отдельно входное звено 1 со стойкой 4 и прилагаем к нему силу тяжести G1 и силу реакции R21 от оторванного шатуна 2 механизма (рис. 8.5).
Векторная сумма всех сил, действующих на входное звено 1, приравнивается нулю: В соответствии с уравнением в масштабе сил строим план сил (рис.8.6), на котором находим реакцию во вращательной кинематической паре А - R4l.
Реакция в кинематической паре A: 8.5. Вопросы для проверки знаний 1. Какие Вы знаете силы и моменты сил, действующие на звенья механизма или машины? 2. Как найти величину и направление силы инерции звена? 3. Как найти величину и направление момента сил инерции звена? 4. Когда сила инерции звена равна нулю? 5. Когда момент силы инерции звена равен нулю? 6. Какие Вы можете привести примеры сил движущих или сил полезных сопротивлений в машинах? 7. Какие компоненты реакций (величина, точка приложения, направление) известны при силовом расчете в низших (вращательных и поступательных) кинематических парах плоского механизма? 8. Какие компоненты реакций (величина, точка приложения, направление) известны при силовом расчете в высших кинематических парах плоского механизма? 9. С какой целью выполняется силовой расчет механизмов? 10. Какие силы и моменты сил обычно известны и какие силы и моменты сил необходимо определить при силовом расчете механизма? 11. В какой последовательности выполняется силовой расчет механизмов? 12. Почему силовой расчет механизмов называют кинето- статическим? 13. В какой последовательности выполняется силовой расчет структурных групп звеньев? 14. В какой последовательности выполняется силовой расчет входного звена механизма? 15. В чем состоит теорема о " жестком рычаге" Н.Е. Жуковского? 16. Что называют уравновешивающим моментом, уравновешивающей силой? 17. К какому звену прилагают уравновешивающий момент? 18. Как выполняют проверку силового расчета механизма? 19. Где используются результаты силового расчета механизма?
9. ОПРЕДЕЛЕНИЕ ОШИБКИ ПОЛОЖЕНИЯ ПЛОСКОГО МЕХАНИЗМА МЕТОДОМ ПЛАНОВ МАЛЫХ ПЕРЕМЕЩЕНИЙ 9.1. Общие сведения о точностном анализе механизма методом планов малых перемещений Теория точности механизмов - это раздел теории механизмов и машин, занимающийся исследованием ошибок механизмов, происходящих от различных факторов, исследованием влияния этих ошибок на кинематику и динамику механизмов и синтезом механизмов с учетом возможных ошибок [1]. Ошибка механизма - это отклонение действительных параметров механизма от теоретических. Теоретический механизм - это тот механизм, у которого все элементы кинематических пар изготовлены абсолютно точно, зазоры в кинематических парах отсутствуют, размеры звеньев не отличаются от заданных номинальных. Спроектированные кинематические схемы механизмов можно назвать теоретическими схемами или теоретическими механизмами. Реальный механизм - это действительно изготовленный механизм. Параметры его могут отличаться от теоретических из-за неточностей изготовления звеньев и кинематических пар, неточности монтажа, износа трущихся элементов в кинематических парах, отличия условий эксплуатации (температуры, влажности окружающей среды) от заданных номинальных условий. Ошибка положения механизма - это разница положения выходных звеньев действительного и соответствующего теоретического механизмов при одинаковых положениях входных звеньев обоих механизмов. Чем меньше ошибка положения механизма, тем более точно механизм воспроизводит необходимый закон движения ведомого звена. Неточность механизма определяется в основном его первичными ошибками, к которым относятся отклонения расстояния между кинематическими элементами звеньев и отклонения размеров элементов, их формы и расположения от теоретических. Суммарная ошибка положения механизма равна сумме ошибок положения, вызываемых каждой первичной ошибкой в отдельности. Для плоских механизмов с низшими кинематическими парами, в которых основное влияние на точность оказывают ошибки размеров звеньев, наиболее удобен для определения ошибки положения механизма метод планов малых перемещений. План малых перемещений имеет сходство с планом скоростей, но при этом есть и отличия, сближающие его с планом ускорений. При построении плана малых перемещений исходят из следующих соображений [2]: 1. Перемещение любой точки действительного механизма обусловлено не движением входного звена, а дефектным (вследствие первичных ошибок в механизме) перемещением всех других точек относительно тех положений, которые они занимали бы в теоретическом механизме. 2. Дефектные перемещения точек являются величинами, не зависимыми друг от друга и вызваны первичными ошибками длин звеньев. Влияние первичных ошибок дополняется перемещением точек, обусловленным связями в механизме. 3. Отклонения размеров звеньев настолько малы, что направления звеньев реального и теоретического механизмов совпадают. Тем самым учитываются ошибки только первого порядка малости. Необходимо научиться составлять векторные уравнения дефектных (малых) перемещений для двух случаев расположения рассматриваемых точек. 1. Две точки (А и В) принадлежат одному звену и удалены друг от друга на расстояние l ba (рис. 9.1). Дефектное перемещение одной точки (например точки А) из- вестно. Требуется определить дефектное перемещение другой точки (точки В). Составляем векторное уравнение малых перемещений точек:
где
Для удобства определения дефектных перемещений дефектное перемещение
Нормальная составляющая Тангенциальная составляющая 2. Две точки (A1и A2) принадлежат разным звеньям (1 и 2), образующим поступательную пару, и в данный момент совпадают (рис. 9.2). Дефектное перемещение одной точки (например точки A1) известно. Требуется определить дефектное перемещение другой точки (точки A2). Составляем векторное уравнение малых перемещений:
где
движения ползуна 2. Так же направлено дефектное (малое) перемещение При построении плана малых перемещений механиз ма считают элемент стойки, с которым соединено ведомое звено, совпадающим со своим теоретическим положением. Этот элемент стойки ошибки положения не имеет. Дефектные положения элементов других кинематических пар находят по отношению к системе координат, связанной с этим элементом стойки. Первичные ошибки механизма при этом должны быть заданы. Для простоты можно считать, что угол φ, определяющий положение ведущего звена, погрешности не имеет. Порядок рассмотрения точек звеньев механизма припостроении плана малых перемещений механизма: вначале рассматривают точки входного звена, то есть того звена, закон движения которого задан. Затем рассматривают точки первой присоединенной к входному звену и стойке структурной группы звеньев, потом второй структурной группы и так далее. Дефектные перемещения точек звеньев находят на основании векторных уравнений малых перемещений. При рассмотрении точек структурных групп составляют систему двух векторных уравнений малых перемещений. В каждом уравнении выражают дефектное перемещение точки, связанной со средней кинематической парой структурной группы. При этом в качестве полюса принимают для одного уравнения одну точку, а для другого уравнения другую точку, которые относятся к крайним кинематическим парам рассматриваемой структурной группы. 9.2. Задание на практическое занятие № 9
Определить ошибку положения выходного звена механизма методом плана малых перемещений. Вариант задания студенту задает преподаватель. В таблице 9.1 для каждого варианта задания дан номер исследуемого механизма, значение угла поворота φ входного звена, определяющее заданное положение механизма, и значения учитываемых первичных ошибок механизма. Схема заданного механизма дана на рис. 9.3. Кинематические схемы на рис. 9.3 изображены в масштабе длин μ l = 0, 004 м/мм (м 1: 4). На схемах показано направление вращения входного звена и обозначен угол поворота φ этого звена.
9.3. Последовательность выполнения задания № 9 9.3. Согласно варианту задания изобразить в принятом масштабе длин кинематическую схему механизма при заданном значении угла поворота φ входного звена. Представить все вычисления и векторные уравнения, необходимые для построения плана малых перемещений механизма. Построить в масштабе план малых перемещений механизма. 9.4. Пример выполнения задания № 9
Задание: Определить ошибку положения выходного звена плоского четырехзвенного механизма методом плана малых перемещений. Исходные данные: Номер схемы исследуемого механизма - 1 (рис. 9.4). Угол поворота входного кривошипа φ = 65°. Первичные ошибки механизма: 1) ошибки положения шарнира А соединения кривошипа AB со стойкой по оси Xи по оси У: Решение: При построении плана малых перемещений будем считать элемент стойки 4, с которым соединено выходное звено- ползун 3, совпадающим со своим идеальным положением. То есть, считаем, что положение направляющей стойки 4 для движения ползуна 3 не имеет ошибки положения. Связываем систему координат (оси У и X), относительно которой будут рассматриваться дефектные перемещения точек звеньев механизма, с точкой C4 стойки, которая в рассматриваемое мгновение у теоретического механизма на кинематической схеме (рис. 9.4) совпадает по положению с точкой С ползуна. Дефектное перемещение точки C4 считаем равным нулю: Вначале рассматриваем точки входного звена 1. Для точки А составляем векторное уравнение малых перемещений:
Так как
Рис. 9.3. Схемы четырехзвенных плоских механизмов Таблица 9.1. Заданные величины для выполнения задания № 9
|

 .
. , или
, или 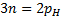 ,
, - количество низших кинематических пар механизма,
- количество низших кинематических пар механизма,  - количество высших кинематических пар механизма.
- количество высших кинематических пар механизма. . Вычисляется тангенциальная составляющая реакции во вращательной паре А -
. Вычисляется тангенциальная составляющая реакции во вращательной паре А - 
 .
. . В соответствии с уравнением в масштабе сил строится план сил, на котором находят нормальные составляющие реакций и полные реакции в крайних кинематических парах А и С:
. В соответствии с уравнением в масштабе сил строится план сил, на котором находят нормальные составляющие реакций и полные реакции в крайних кинематических парах А и С:  .
.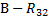 .
. . Вычисляется тангенциальная составляющая реакции во вращательной паре
. Вычисляется тангенциальная составляющая реакции во вращательной паре  .
. .
. .
. , действующей в поступательной паре Д, относительно точки
, действующей в поступательной паре Д, относительно точки  .
.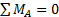 .
.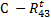 . Векторная сумма всех сил, действующих на звено 3, приравнивается нулю:
. Векторная сумма всех сил, действующих на звено 3, приравнивается нулю:  . В соответствии с уравнением в масштабе сил строится план сил, на котором находят нормальную составляющую реакции и полную реакцию в крайней вращательной кинематической паре С, и реакцию в поступательной паре:
. В соответствии с уравнением в масштабе сил строится план сил, на котором находят нормальную составляющую реакции и полную реакцию в крайней вращательной кинематической паре С, и реакцию в поступательной паре:  .
. .
. , действующей в поступательной паре, относительно точки
, действующей в поступательной паре, относительно точки  .
. .
. .
. Рис. 8.1. Схемы структурных групп звеньев
Рис. 8.1. Схемы структурных групп звеньев


 (8.4)
(8.4) - момент инерции звена относительно его центра тяжести,
- момент инерции звена относительно его центра тяжести,  ; l - длина звена, м.
; l - длина звена, м. ; 2) если выходное звено совершает вращательное движение, то на него действует момент сил полезного сопротивления
; 2) если выходное звено совершает вращательное движение, то на него действует момент сил полезного сопротивления  . Сила и момент сил полезного сопротивления направлены в сторону, противоположную направлению скорости движения звена приложения.
. Сила и момент сил полезного сопротивления направлены в сторону, противоположную направлению скорости движения звена приложения. представлена на рис. 6.4 и 7.4.
представлена на рис. 6.4 и 7.4. .
.

 .
.
 точки С относительно условно неподвижной точки В. Угловое ускорение ε 2 звена AB направлено в ту же сторону, что и вектор
точки С относительно условно неподвижной точки В. Угловое ускорение ε 2 звена AB направлено в ту же сторону, что и вектор 

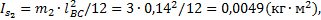
 - момент инерции звена ВС относительно его центра тяжести;
- момент инерции звена ВС относительно его центра тяжести;  - длина звена ВС;
- длина звена ВС; 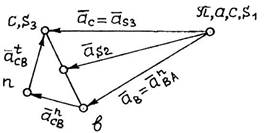 Рис. 8.2. План ускорений кривошипно-ползунного механизма
Рис. 8.2. План ускорений кривошипно-ползунного механизма
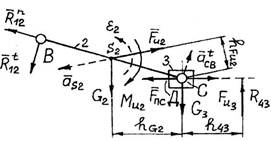 Рис. 8.3. Схема структурной группы звеньев 2-3
Рис. 8.3. Схема структурной группы звеньев 2-3





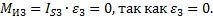
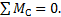 Вычисляется тангенциальная составляющая реакции во вращательной паре
Вычисляется тангенциальная составляющая реакции во вращательной паре 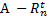 .
.

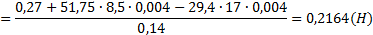
 .
.
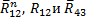 . План сил строим в масштабе μ Ρ = 6 H/ мм. Чтобы определить длину вектора силы, величину этой силы делим на этот масштаб. Например, силу тяжести шатуна 2 откладываем на плане сил в виде отрезка длиной G2/μ F = 29, 4/6 = 4, 9 мм. Находим на плане неизвестные реакции, умножая измеренные на плане длины соответствующих векторов на масштаб плана сил:
. План сил строим в масштабе μ Ρ = 6 H/ мм. Чтобы определить длину вектора силы, величину этой силы делим на этот масштаб. Например, силу тяжести шатуна 2 откладываем на плане сил в виде отрезка длиной G2/μ F = 29, 4/6 = 4, 9 мм. Находим на плане неизвестные реакции, умножая измеренные на плане длины соответствующих векторов на масштаб плана сил:


 Рис. 8.4. План сил структурной группы звеньев 2-3
Рис. 8.4. План сил структурной группы звеньев 2-3
 .
.
 замыкает уже имеющуюся на плане
замыкает уже имеющуюся на плане
 Рис. 8.5. Схема входного звена механизма
Рис. 8.5. Схема входного звена механизма
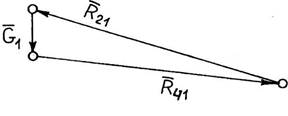 Рис. 8.6. План сил входного звена механизма
Рис. 8.6. План сил входного звена механизма
 . Условный уравновешивающий момент в данной работе не определяем и проверку силового расчета по теореме Н.Е. Жуковского не выполняем.
. Условный уравновешивающий момент в данной работе не определяем и проверку силового расчета по теореме Н.Е. Жуковского не выполняем. (9.1)
(9.1) - соответственно векторы дефектных перемещений точки В, точки А, точки В относительно условно неподвижной точки А, взятой в качестве полюса.
- соответственно векторы дефектных перемещений точки В, точки А, точки В относительно условно неподвижной точки А, взятой в качестве полюса. Рис. 9.1. Дефектные (малые) перемещения в относительном движении двух точек, лежащих на одном звене
Рис. 9.1. Дефектные (малые) перемещения в относительном движении двух точек, лежащих на одном звене
 в уравнении (9.1) раскладывают на две составляющие: нормальную
в уравнении (9.1) раскладывают на две составляющие: нормальную  и тангенциальную
и тангенциальную  . Уравнение (9.1) при этом принимает следующий вид:
. Уравнение (9.1) при этом принимает следующий вид: (9.2)
(9.2) направлена по прямой, соединяющей рассматриваемые точки; стрелка вектора направлена от точки В, движение которой рассматривается, к точке А, которая взята за полюс в рассматриваемом относительном движении, или наоборот. Нормальное дефектное перемещение всегда известно по величине и направлению (это заданное отклонение длины действительного звена от длины теоретического звена). Направление стрелки этого вектора зависит от знака заданной ошибки длины l BA этого звена (рис. 9.1): при положительном знаке стрелка вектора направлена от точки А к точке В, а при отрицательном знаке - от точки В к точке А.
направлена по прямой, соединяющей рассматриваемые точки; стрелка вектора направлена от точки В, движение которой рассматривается, к точке А, которая взята за полюс в рассматриваемом относительном движении, или наоборот. Нормальное дефектное перемещение всегда известно по величине и направлению (это заданное отклонение длины действительного звена от длины теоретического звена). Направление стрелки этого вектора зависит от знака заданной ошибки длины l BA этого звена (рис. 9.1): при положительном знаке стрелка вектора направлена от точки А к точке В, а при отрицательном знаке - от точки В к точке А. обычно известна только по направлению: она направлена перпендикулярно прямой BA звена (рис 9.1). Тангенциальное дефектное перемещение
обычно известна только по направлению: она направлена перпендикулярно прямой BA звена (рис 9.1). Тангенциальное дефектное перемещение  имеет место ввиду ошибки dφ в угловом положении звена.
имеет место ввиду ошибки dφ в угловом положении звена. (9.3)
(9.3) - соответственно малые перемещения точки A2, точки A1 и точки A2 относительно условно неподвижной точки A1, взятой в качестве полюса. Движение точки A2 относительно точки A1 можно рассмотреть на рис.9.2. Точка A2 движется по прямой линии, параллельной направляющей
- соответственно малые перемещения точки A2, точки A1 и точки A2 относительно условно неподвижной точки A1, взятой в качестве полюса. Движение точки A2 относительно точки A1 можно рассмотреть на рис.9.2. Точка A2 движется по прямой линии, параллельной направляющей Рис. 9.2. Дефектные (малые) перемещения в относительном движении двух точек, принадлежащих разным звеньям, входящим в поступательную пару
Рис. 9.2. Дефектные (малые) перемещения в относительном движении двух точек, принадлежащих разным звеньям, входящим в поступательную пару
 . Известно лишь направление вектора.
. Известно лишь направление вектора. ;
;  ; 2) ошибки длин звеньев (кривошипа AB и шатуна ВС):
; 2) ошибки длин звеньев (кривошипа AB и шатуна ВС): 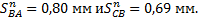
 , поэтому на плане малых перемещений (рис. 9.5) обозначаем точку с4, совпадающую с полюсом плана p.
, поэтому на плане малых перемещений (рис. 9.5) обозначаем точку с4, совпадающую с полюсом плана p.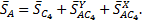
 , то это уравнение принимает вид
, то это уравнение принимает вид





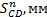
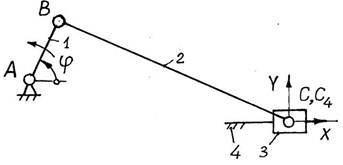 Рис. 9.4. Кинематическая схема плоского четырехзвенного кривошипно-ползунного механизма
Рис. 9.4. Кинематическая схема плоского четырехзвенного кривошипно-ползунного механизма



