Две точки ( A1 и A2) принадлежат разным звеньям (1 и 2), образующим поступательную пару, и в данный момент совпадают
Скорость одной точки (например точки A 1) известна. Требуется определить скорость другой точки (точки A 2 ). Составляем векторное уравнение скоростей:
где
Скорость точки Порядок рассмотрения точек звеньев механизма при построении плана скоростей: вначале рассматривают точки входного звена, то есть того звена, закон движения которого задан. Затем рассматривают точки первой присоединенной к входному звену и стойке структурной группы звеньев, потом второй структурной группы и так далее. Скорости точек звеньев находят на основании векторных уравнений скоростей. При рассмотрении точек структурных групп составляют систему двух векторных уравнений скоростей. В каждом уравнении выражают скорость точки, связанной со средней кинематической парой структурной группы. При этом в качестве полюса принимают для одного уравнения одну точку, а для другого уравнения другую точку, которые относятся к крайним кинематическим парам рассматриваемой структурной группы. Входное звено механизма обычно совершает вращательное движение относительно стойки. Считают, что это движение является равномерным. Частота вращения входного звена
7.2. Основные понятия и уравнения для построения плана ускорений механизма Основные задачи данного метода — определение линейных ускорений точек звеньев механизма по заданной кинематической схеме механизма и заданному закону движения входного звена. Все размеры звеньев механизма должны быть известны. Линейные ускорения точек звеньев механизма необходимо знать для определения сил инерции звеньев при решении задачи кинетостатического (силового) расчета машин. Определение ускорений выполняется графически: путем построения в масштабе многоугольника, составленного из векторов ускорений (плана ускорений). План ускорений строится для конкретного положения механизма на основании векторных уравнений ускорений. При построении плана ускорений так же, как и при построении плана скоростей, рассматривают обычно лишь точки звеньев, совпадающие с кинематическими парами. тельного вращательного движения вокруг этого полюса. За полюс принимается обычно точка, ускорение которой известно. Необходимо научиться составлять векторные уравнения ускорений для двух случаев расположения рассматриваемых точек. 1. Две точки (А и В) принадлежат одному звену и удалены друг от друга на расстояние lBA. Ускорение одной точки (например точки А) известно. Требуется определить ускорение другой точки (точки В). Составляем векторное уравнение ускорений:
где Ускорение точки В относительно условно неподвижной точки А можно рассмотреть на рис. 7.3. При относительном вращательном движении звена вокруг точки А точка В движется по дуге окружности, описанной из точки А. Для удобства определения ускорений ускорение
Уравнение (7.4) при этом принимает следующий вид:
Нормальная составляющая
где ω - угловая скорость звена, на котором расположены рассматриваемые точки, с-1.
Тангенциальная составляющая Величину тангенциальной составляющей ускорения можно определить по формуле
где ε - угловое ускорение звена, на котором расположены рассматриваемые точки, с-2; l ВА - расстояние между точками В и А, м. 2. Две точки (A1 и A2)принадлежат разным звеньям (1 и 2), образующим поступательную пару, и в данный момент совпадают. Ускорение одной точки (например точки A1) известно. Требуется определить ускорение другой точки (точки A2 ). Составляем векторное уравнение ускорений:
где точки A1 и точки A2 относительно условно неподвижной точки A1, взятой в качестве полюса. Ускорение точки A2 относительно точки A1 можно рассмотреть на рис. 7.4.
Для удобства определения ускорений ускорение в относительном движении рассматриваемых точек в этом случае раскладывают на две составляющие: кориолисово ускорение Уравнение (7.9) при этом принимает следующий вид:
Кориолисово ускорение появляется вследствие того, что переносное движение является вращательным. Кориолисово ускорение при плоском движении звеньев можно вычислить по формуле:
Для определения направления кориолисова ускорения необходимо вектор относительной скорости Порядок рассмотрения точек звеньев механизма при построении плана ускорений остается тем же, что и при построении плана скоростей: вначале рассматривают точки входного звена, то есть того звена, закон движения которого задан. Затем рассматривают точки первой присоединенной к входному звену и стойке структурной группы звеньев, потом второй структурной группы и так далее.
Ускорения точек звеньев находят на основании векторных уравнений ускорений. При рассмотрении точек структурных групп составляют систему двух векторных уравнений ускорений. В каждом уравнении выражают ускорение точки, связанной со средней кинематической парой структурной группы. При этом в качестве полюса принимают для одного уравнения одну точку, а для другого уравнения другую точку, которые относятся к крайним кинематическим парам рассматриваемой структурной группы; ускорения точек, взятых в качестве полюса, должны быть известны. Входное звено механизма обычно совершает вращательное движение относительно стойки. Считают, что это движение является равномерным. Частота вращения входного звена " nl" дана. Угловую скорость " ω 1" находят по формуле (2.4). 7.3. Задание на практическое занятие № 7
Выполнить кинематическое исследование заданного на рис.7.6 плоского четырехзвенного механизма методом построения плана скоростей и ускорений. Номер схемы студенту задает преподаватель. На схеме показано направление вращения входного звена. Частота вращения входного звена n=150 мин-1. Кинематические схемы на рис. 7.6 изображены в масштабе длин μ l = 0, 004 м / мм (м 1: 4).
Рис. 7.6
Рис. 7.6. (Продолжение)
Рис.7.6. (Окончание)
7.4. Последовательность выполнения задания №7 Изобразить заданную кинематическую схему четырехзвенного плоского механизма (рис.7.6). Обозначить на схеме номера всех звеньев. Обозначить прописными (большими) буквами все точки, совпадающие с кинематическими парами, скорости и ускорения которых будут определены методом построения плана скоростей и ускорений механизма. Представить все формулы, вычисления и векторные уравнения, необходимые для построения плана скоростей и ускорений.
7.5. Пример выполнения задания № 7 Задание: Выполнить построение плана скоростей и плана ускорений плоского четырехзвенного механизма, схема которого в масштабе длин
Решение: Выполняем построение плана скоростей Вычисляем по формуле (2.4) угловую скорость входного звена 1:
Измеряем длину входного звена - кривошипа 1 на кинематической схеме механизма: AB= 17, 5 мм. Учитывая маc-штаб длин схемы, вычисляем истинную длину звена AB по формуле
Определяем теперь линейные скорости точек звеньев путем построения плана скоростей механизма (рис. 7.8). Изображаем точку " р" полюса плана скоростей. Из этой точки будем проводить векторы абсолютных скоростей точек звеньев механизма. Точки на концах этих векторов необходимо обозначить строчными (малыми) буквами, соответствующими рассматриваемым точкам схемы механизма.
Рассматриваем вначале скорости точек входного звена AB. Скорость точки А равна нулю, так как эта точка неподвижна при работе механизма: Va= 0. Вектор скорости Для определения скорости точки В составляем векторное уравнение скоростей (7.1): VA=0, то Величину этой скорости определяем по формуле (7.2):
Вектор
Рассматриваем далее точки структурной группы звеньев 2-3: В, С и C4. В поступательной кинематической паре соединения звеньев 3 и 4 обозначены две точки: подвижная точка С, принадлежащая звену 3, и неподвижная точка C4, принадлежащая звену 4 (стойке). Обе эти точки в рассматриваемое мгновение по положению совпадают. Скорость точки С необходимо определить. Скорости же двух остальных точек известны: скорость точки В найдена и ее вектор на плане скоростей уже проведен, скорость же точки С4 стойки равна нулю, поэтому на плане скоростей обозначаем точку С4, совпадающую с полюсом плана - точкой p (рис. 7.8). Составляем систему двух векторных уравнений скоростей:
Приравниваем правые части этих двух уравнений (7.12), так как левые части их равны:
Так как
В этом уравнении абсолютная скорость
направляющей относительного поступательного движения звеньев 3 и 4, то есть параллельна линии AC механизма (рис.7. 7). В соответствии с уравнением (7.13) из конца вектора скорости Вычисляем величины неизвестных скоростей:
Выполняем построение плана ускорений Рассматриваем заданную схему кривошипно-ползунного механизма (рис. 7.9). Рядом изображаем точку π полюса плана скоростей (рис. 7.10). Из этой точки будем проводить векторы абсолютных ускорений точек звеньев механизма. Точки на концах этих векторов необходимо обозначить строчными (малыми) буквами, соответствующими рассматриваемым точкам схемы механизма. Рассматриваем вначале ускорения точек входного звена АВ. Ускорение точки А равно нулю, так как эта точка неподвижна при работе механизма: аА = 0. На плане ускорений вектор ускорения Для определения ускорения точки В составляем векторное уравнение ускорений (7.5)
Величину тангенциальной составляющей ускорения определяем по формуле (7.8)
где ε - угловое ускорение звена, на котором расположены рассматриваемые точки, с-2;
По заданию вращение входного звена механизма (кривошипа АВ) равномерное, поэтому тангенциальная составляющая ускорения точки В относительно точки А равна нулю. Так как Величину этого ускорения определяем по формуле (7.6):
Вектор Принимаем, например,
Рассматриваем далее точки структурной группы звеньев 2-3: В, С и C4.В поступательной кинематической паре соединения звеньев 3 и 4 обозначены две точки: подвижная точка С принадлежащая звену 3, и неподвижная точка C4, принадлежащая звену 4 (стойке). Обе эти точки в рассматриваемое мгновение по положению совпадают. Ускорение точки С необходимо определить. Ускорения же двух остальных точек известны: ускорение точки В найдено и его вектор на плане ускорений уже проведен, ускорение же точки C4 стойки равно нулю. На плане ускорений обозначаем точку с4, которая совпадает с полюсом плана - точкой π (рис. 7.10). Используя зависимости (7.5) и (7.10), составляем систему двух векторных уравнений ускорений
Приравниваем правые части этих двух уравнений, так как левые части их равны:
Вычисляя кориолисово ускорение по формуле (7.11), видим, что оно равно нулю, так как ползун 3 и направляющая стойки 4, входящие в поступательную кинематическую пару, вращательного движения совершать не могут:
Так как
Величину и направление нормальной составляющей ускорения
Вектор схеме механизма и направлен от точки С, движение которой рассматривается, к точке В, принятой в качестве полюса (рис. 7.9). Так как по уравнению (7.15) эту составляющую необходимо прибавить к ускорению точка b на конце вектора
Проводим этот вектор. По уравнению (7.15) необходимо далее прибавить вектор тангенциальной составляющей ускорения По уравнению (7.15) на плане ускорений необходимо провести еще релятивное ускорение Вычисляем величины неизвестных ускорений:
7.6. Вопросы для проверки знаний
1. Что называют планом скоростей механизма? 2. Скорости каких точек звеньев находят при построении плана скоростей механизма? 3. Какие два случая расположения рассматриваемых точек встречаются при построении плана скоростей механизма? 4. Какой вид имеет формула, связывающая угловую скорость звена и частоту его вращения? 5. По какой формуле можно вычислить линейную скорость точки кривошипа? 6. Какой вид имеет векторное уравнение, связывающее скорости двух точек, принадлежащих одному звену? 7. Какой вид имеет векторное уравнение, связывающее скорости двух совпадающих точек, принадлежащих двум звеньям, образующим поступательную кинематическую пару? 8. В какой последовательности рассматриваются точки звеньев при построении плана скоростей плоского механизма? 9. Какую размерность имеет масштаб плана скоростей механизма? 10. С какой целью определяют линейные скорости точек звеньев? 11. Что называют планом ускорений механизма? 12. Ускорения каких точек звеньев находят при построении плана ускорений механизма? 13. Какие два случая расположения рассматриваемых точек встречаются при построении плана ускорений механизма? 14. Какой вид имеют формулы для вычисления нормальной составляющей ускорения в относительном движении двух точек, принадлежащих одному звену и разделенных каким то расстоянием? 15. Как направлен вектор нормальной составляющей ускорения в относительном движении двух точек, принадлежащих одному звену? 16. Какой вид имеет векторное уравнение, связывающее ускорения двух точек, принадлежащих одному звену? 17. Какой вид имеет векторное уравнение, связывающее ускорения двух совпадающих точек, принадлежащих двум звеньям, образующим поступательную кинематическую пару? 18. Какой вид имеет формула для вычисления тангенциальной составляющей ускорения в относительном движении двух точек, принадлежащих одному звену? 19. Как направлен вектор тангенциальной составляющей ускорения в относительном движении двух точек, принадлежащих одному звену? 20. По какой формуле вычисляют кориолисово ускорение в относительном движении двух совпадающих точек, принадлежащих, двум звеньям, образующим поступательную кинематическую пару? 21. Как определяют направление вектора кориолисова ускорения в относительном движении двух точек, принадлежащих двум звеньям, образующим поступательную кинематическую пару? 22. Как направлен вектор релятивного ускорения в относительном движении двух точек, принадлежащих двум звеньям? 23. В какой последовательности рассматриваются точки звеньев при построении плана ускорений плоского механизма? 24. Какую размерность имеет масштаб плана ускорений механизма? 25. С какой целью определяют линейные ускорения точек звеньев?
8. КИНЕТОСТАТИЧЕСКИЙ (СИЛОВОЙ) РАСЧЕТ ПЛОСКОГО МЕХАНИЗМА 8.1. Силы и моменты сил, действующие на звенья механизма, последовательность силового расчета механизма
Силовой расчет механизмов заключается в определении сил и моментов сил, действующих на звенья. Величины сил и моментов сил, действующих на звенья, используются для дальнейших расчетов деталей механизмов на прочность и определения деформации упругих элементов. По величине сил, действующих в кинематических парах механизма, устанавливают потери на трение и определяют коэффициент полезного действия механизма. В дальнейшем будут называться лишь силы, однако излагаемые сведения относятся и к моментам сил. Силы, действующие на звенья, условно делят на две группы: движущие силы и силы сопротивления. Силы движущие (Fд) — это силы, которые создают и поддерживают движение; работа этих сил положительна. Примеры этих сил: сила давления жидкости на поршень гидроцилиндра, сила давления сжатого воздуха на поршень пневмоцилиндра, сила давления газов при сгорании топлива на такте рабочего хода двигателя внутреннего сгорания автомашины, тепловоза, трактора, экскаватора, вертолета. Силы сопротивления (Fc)- это силы, которые препятствуют движению звеньев механизма; работа этих сил отрицательна. Силы сопротивления могут быть полезными и вредными. Силы полезных сопротивлений (Fпс) - это силы, для преодоления которых предназначена машина или прибор (например, сила тяжести маятника часов, силы сопротивления материала его резанию в металлорежущих или деревообрабатывающих станках, силы сопротивления материала его деформации при прессовании и др.). Силы вредных сопротивлений (Fис) - это силы, на преодоление которых непроизводительно затрачивается работа движущих сил (например, силы трения в кинематических парах механизма). Кроме сил движущих и сил сопротивления в механизме действуют также силы тяжести и силы инерции звеньев, а также внутренние силы - силы давления (реакции) в кинематических парах. Сила тяжести звена (G)может быть найдена по формуле
где т - масса звена, кг.; g - ускорение свободного падения В общем случае при любом виде движения звена для учета действия сил инерции можно определять силу инерции звена (Fu), приложенную в центре тяжести, и момент сил инерции звена (Mu), действующий на звено, по следующим формулам:
где т - масса звена, кг; as - ускорение точки центра тяжести звена, м/с; Is - момент инерции звена относительно его центра тяжести, кг ε - угловое ускорение звена, с-1. Вектор силы инерции звена направлен в сторону, противоположную вектору ускорения центра тяжести звена. Момент сил инерции звена направлен в сторону,
|

 , (7.3)
, (7.3) Рис. 7.2. Скорость в относительном движении двух точек, принадлежащих разным звеньям, входящим в поступательную пару
Рис. 7.2. Скорость в относительном движении двух точек, принадлежащих разным звеньям, входящим в поступательную пару
 - соответственно векторы скоростей точки
- соответственно векторы скоростей точки  точки
точки  и точки
и точки  .
. дана. Угловую скорость
дана. Угловую скорость 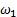 находят по формуле (2.4):
находят по формуле (2.4):
 (7.4)
(7.4) - соответственно векторы скоростей точки В, точки А, точки В относительно условно неподвижной точки А, взятой в качестве полюса.
- соответственно векторы скоростей точки В, точки А, точки В относительно условно неподвижной точки А, взятой в качестве полюса. раскладывают в этом случае на две составляющие: нормальную
раскладывают в этом случае на две составляющие: нормальную  и тангенциальную
и тангенциальную  .
. Рис. 7.3. Ускорение в относительном движении двух точек, лежащих на одном звене
Рис. 7.3. Ускорение в относительном движении двух точек, лежащих на одном звене
 (7.5 )
(7.5 ) , (7.6)
, (7.6) (7.7 )
(7.7 )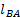 - расстояние между рассматриваемыми точками, м;
- расстояние между рассматриваемыми точками, м;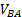 - линейная скорость движения точки В относительно точки А, м/с.
- линейная скорость движения точки В относительно точки А, м/с. , (7.8)
, (7.8) (7.9)
(7.9) соответственно векторы ускорений точки A2,
соответственно векторы ускорений точки A2, Рис. 7.4. Ускорение в относительном движении двух точек, принадлежащих разным звеньям, входящим в поступательную пару
Рис. 7.4. Ускорение в относительном движении двух точек, принадлежащих разным звеньям, входящим в поступательную пару
 и релятивное ускорение
и релятивное ускорение  .
.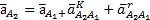 (7.10)
(7.10)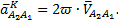 (7.11)
(7.11) повернуть на 90° по направлению угловой скорости
повернуть на 90° по направлению угловой скорости  звеньев (рис. 7.5). Полученное направление вектора совпадает с направлением вектора кориолисова ускорения
звеньев (рис. 7.5). Полученное направление вектора совпадает с направлением вектора кориолисова ускорения  Рис. 7.5. Картина определения направления вектора кориолисова ускорения
Рис. 7.5. Картина определения направления вектора кориолисова ускорения

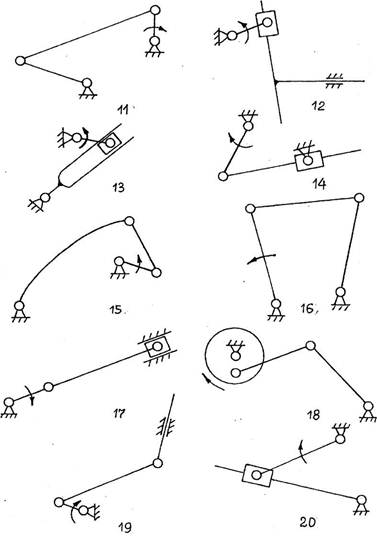


 (М 1: 4) представлена на рис. 7.7. Входное звено механизма - кривошип АВ. Частота вращения входного звена n1 = 150мин-1. Направление вращения входного звена на схеме показано.
(М 1: 4) представлена на рис. 7.7. Входное звено механизма - кривошип АВ. Частота вращения входного звена n1 = 150мин-1. Направление вращения входного звена на схеме показано. Рис. 7.7. Кинематическая схема плоского четырехзвенного кривошипно-ползунного механизма
Рис. 7.7. Кинематическая схема плоского четырехзвенного кривошипно-ползунного механизма
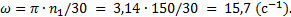

 Рис. 7.8. План скоростей кривошипно-ползунного механизма
Рис. 7.8. План скоростей кривошипно-ползунного механизма
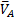 на плане скоростей поэтому отсутствует; точка а на плане скоростей совпадает с полюсом р.
на плане скоростей поэтому отсутствует; точка а на плане скоростей совпадает с полюсом р.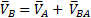 . Так как
. Так как .
.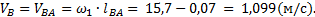
 (рис. 7.8) перпендикулярен линии BA звена на схеме механизма и направлен в сторону заданной угловой скорости этого звена (рис. 7.7). Задаемся длиной этого вектора в зависимости от наличия места для плана скоростей и проводим этот вектор. Принимаем, например, pa = 32 мм. Тогда масштаб плана скоростей будет:
(рис. 7.8) перпендикулярен линии BA звена на схеме механизма и направлен в сторону заданной угловой скорости этого звена (рис. 7.7). Задаемся длиной этого вектора в зависимости от наличия места для плана скоростей и проводим этот вектор. Принимаем, например, pa = 32 мм. Тогда масштаб плана скоростей будет: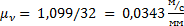 .
.
 . (7.12)
. (7.12) .
. , то полученное уравнение можно представить в виде:
, то полученное уравнение можно представить в виде: . (7.13)
. (7.13) уже известна, а скорости в относительном движении точек
уже известна, а скорости в относительном движении точек 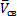 и
и  известны только по направлению. Так как точки С и В принадлежат одному и тому же звену 2, то
известны только по направлению. Так как точки С и В принадлежат одному и тому же звену 2, то 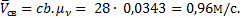

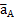 поэтому отсутствует; точка а на плане ускорений совпадает с полюсом π.
поэтому отсутствует; точка а на плане ускорений совпадает с полюсом π. .
. Рис. 7.9. Кинематическая схема плоского четырехзвенного кривошипно-ползунного механизма
Рис. 7.9. Кинематическая схема плоского четырехзвенного кривошипно-ползунного механизма
 Рис. 7.10. План ускорений кривошипно-ползунного механизма
Рис. 7.10. План ускорений кривошипно-ползунного механизма


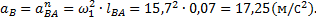
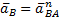 (рис. 7.10) параллелен линии BA звена на схеме механизма и направлен от точки В, движение которой рассматривается, к точке А, принятой в качестве полюса (рис. 7.9). Задаемся длиной этого вектора в зависимости от наличия места для плана ускорений и проводим этот вектор.
(рис. 7.10) параллелен линии BA звена на схеме механизма и направлен от точки В, движение которой рассматривается, к точке А, принятой в качестве полюса (рис. 7.9). Задаемся длиной этого вектора в зависимости от наличия места для плана ускорений и проводим этот вектор. . Тогда масштаб плана ускорений будет:
. Тогда масштаб плана ускорений будет:
 .
. .
. (7.14)
(7.14) .
.
 и
и  , то уравнение (7.14) можно представить в виде:
, то уравнение (7.14) можно представить в виде: (7.15)
(7.15) можно определить. Величину этого ускорения определяем по формуле (7.7):
можно определить. Величину этого ускорения определяем по формуле (7.7):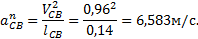
 , то на плане ускорений
, то на плане ускорений
 , поэтому из точки nплана ускорений (рис. 7.10) проводим линию вектора
, поэтому из точки nплана ускорений (рис. 7.10) проводим линию вектора  , направление которого известно: оно параллельно направляющей относительного поступательного движения звеньев 3 и 4, то есть параллельно линии AC механизма (рис. 7.9). Величина вектора неизвестна. Этот вектор должен соединять на плане ускорений точки c4и с. Поэтому из точки c4, совпадающей с полюсом плана ускорений π (рис. 7.10), проводим линию вектора
, направление которого известно: оно параллельно направляющей относительного поступательного движения звеньев 3 и 4, то есть параллельно линии AC механизма (рис. 7.9). Величина вектора неизвестна. Этот вектор должен соединять на плане ускорений точки c4и с. Поэтому из точки c4, совпадающей с полюсом плана ускорений π (рис. 7.10), проводим линию вектора 



 (8.1)
(8.1) .
. (8. 2)
(8. 2) (8.3)
(8.3) м2;
м2;


