Решение. 1. Угловая скорость валов находится по формуле (6.9):
1. Угловая скорость валов находится по формуле (6.9):
2. Передаваемый номинальный вращающий момент находится по формуле (6.10):
3. По формуле (6.1) определяем диаметр соединяемых концов валов, принимая допускаемое напряжение на кручение
Принимаем d = 15 мм. 4. Вычисляем расчетный вращающий момент для муфты по формуле (6.2). При неравномерном вращении валов, средней величине ускоряемых масс и спокойной нагрузке коэффициент режима
5. По табл. 6.1, выполняя условия (6.3), выбираем стандартную упругую муфту со звездочкой. Параметры муфты:
6. По табл. 6.2 находим размеры поперечного сечения призматической шпонки по значению диаметра вала 7. По формуле (6.5) определяем длину шпонки.
Это значение длины имеется в стандартном ряду значений длин шпонок, приведенном в разделе 6.1. 8. Используем шпонку с закругленными торцами. Рабочая длина шпонки находится по формуле (6.7)
9. Проверяем шпоночное соединение по формуле (6.6) по условию прочности на смятие. Принимаем стальные ступицы полумуфт. При спокойной нагрузке допускаемое напряжение
10. По формуле (6.8) проверяем шпоночное соединение по условию прочности шпонки на срез. Допускаемое напряжение на срез при спокойной нагрузке Принимаем
Условия прочности принятого шпоночного соединения вала с полумуфтой выполнены. 6.5. Вопросы для проверки знаний 1. Что называют валом? 2. Что называют осью? 3. Чем отличается вал от оси? 4. Какие напряжения возникают при работе в материале вала и оси? 5. Какие валы бывают по форме геометрической оси? 6. Как можно приближенно вычислить диаметр вала? 7. Что называют муфтой? 8. Какие бывают муфты по конструкции? 9. Чем отличаются сцепные муфты от постоянных? 10. Что является исходными данными для выбора стандартной муфты? 11. Что вычисляют при выборе стандартной муфты? 12. Какие условия требуется выполнить при выборе стандартной муфты по таблице? 13. Что называют шпоночным соединением? 14. Какие бывают виды шпоночных соединений? 15. Какова последовательность определения размеров шпонки? 16. Что является основным критерием работоспособности шпоночного соединения? 17. Какие напряжения проверяют при расчете шпоночного соединения? 18. Какие особенности расчета шпоночного соединения, работающего со слабыми толчками или при ударной нагрузке?
7. КИНЕМАТИЧЕСКОЕ ИССЛЕДОВАНИЕ ПЛОСКОГО МЕХАНИЗМА МЕТОДОМ ПОСТРОЕНИЯ ПЛАНА СКОРОСТЕЙ И УСКОРЕНИЙ 7.1. Основные понятия и уравнения для построения плана скоростей механизма Основные задачи данного метода - определение линейных скоростей точек звеньев механизма по заданной кинематической схеме механизма и заданному закону движения входного звена. Все размеры звеньев механизма должны быть известны. Линейные скорости точек звеньев механизма необходимо знать для определения кинетической энергии механизма при решении задач динамики машин. Они необходимы также для определения угловых скоростей звеньев, вычисления тангенциальных составляющих линейных ускорений в относительном движении точек звеньев. Определение скоростей выполняется графически: путем построения в масштабе многоугольника, составленного из векторов скоростей (плана скоростей). План скоростей строится для конкретного положения механизма на основании векторных уравнений скоростей. При построении плана скоростей механизма рассматривают обычно лишь точки звеньев, совпадающие с кинематическими парами. Например, рассматривают точки звеньев, располагающиеся в центрах вращательных кинематических пар (шарниров). Рассмотрим основные уравнения, используемые для построения плана скоростей. Из теоретической механики известно, что скорость любой точки абсолютно твердого тела можно представить как геометрическую сумму скоростей переносного и относительного движений. В плоском механизме каждое звено в общем случае совершает плоскопараллельное движение, которое можно представить как состоящее из переносного движения вместе с произвольно выбранным полюсом и движения относительно этого полюса. За полюс принимается обычно точка, скорость которой известна. Чтобы применять графические методы кинематического исследования механизма, необходимо научиться составлять векторные уравнения скоростей для двух случаев расположения рассматриваемых точек. 1. Две точки (А и В) принадлежат одному звену и удалены друг от друга на расстояние lBA. Скорость одной точки (например точки А) известна. Требуется определить скорость другой точки (точки В). Составляем векторное уравнение скоростей:
где При относительном вращательном движении звена вокруг точки А точка В движется по дуге окружности, описанной из точки А. Поэтому скорость Величину этой скорости можно найти по формуле
где ω - угловая скорость звена, на котором расположены рассматриваемые точки, с-1; l BA - расстояние между рассматриваемыми точками, м.
|





 Принимаем
Принимаем 
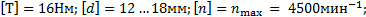

 :
:  . Длина шпонки l = 10...56 мм.
. Длина шпонки l = 10...56 мм.

 . Принимаем
. Принимаем  . По табл. 6, 2 находим для выбранной шпонки справочный размер К для расчета на смятие:
. По табл. 6, 2 находим для выбранной шпонки справочный размер К для расчета на смятие: 




 , (7.1)
, (7.1) - соответственно векторы скоростей точки В, точки А, точки В относительно условно неподвижной точки А, взятой в качестве полюса. Движение точки В относительно точки А можно рассмотреть на рис. 7.1.
- соответственно векторы скоростей точки В, точки А, точки В относительно условно неподвижной точки А, взятой в качестве полюса. Движение точки В относительно точки А можно рассмотреть на рис. 7.1.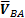 направлена по касательной к дуге этой окружности в точке В, то есть перпендикулярно прямой АВ. Направление скорости соответствует направлению угловой скорости звена ω, и наоборот.
направлена по касательной к дуге этой окружности в точке В, то есть перпендикулярно прямой АВ. Направление скорости соответствует направлению угловой скорости звена ω, и наоборот. (7.2)
(7.2) Рис. 7.1. Скорость в относительном движении двух точек, лежащих на одном звене
Рис. 7.1. Скорость в относительном движении двух точек, лежащих на одном звене



