Теория рассматриваемого вопроса. В реальных условиях передача тепла обычно осуществляется одновременно тремя способами: теплопроводностью
В реальных условиях передача тепла обычно осуществляется одновременно тремя способами: теплопроводностью, конвекцией и излучением (радиацией). Такой вид передачи тепла получил название сложного теплообмена. При этом в разных условиях некоторые его составляющие могут оказывать незначительное влияние на теплообмен и в практических расчётах ими можно пренебрегать. Конвекция происходит только в жидкой или газообразной средах. Этот процесс переноса теплоты осуществляется при перемещении и перемешивании всей массы неравномерно нагретой среды. При этом если движение среды обусловлено разностью плотностей (неравномерностью нагрева), то такой процесс называют свободной (естественной) конвекцией. Если же перемещение среды осуществляется искусственно (за счёт работы насоса, вентилятора и т.п.), то такой процесс называют вынужденной конвекцией. Конвекция всегда сопровождается теплопроводностью. Одновременный перенос теплоты конвекцией и теплопроводностью называют конвективным теплообменом (теплоотдачей). Основной величиной, подлежащей опытному исследованию в конвективном теплообмене, является коэффициент теплоотдачи. В настоящей работе для определения коэффициента теплоотдачи применяется метод регулярного режима (нестационарный процесс теплообмена). При этом экспериментально определяется лишь одна величина – темп охлаждения. К примеру, в исследуемой установке охлаждение тела (стальной трубы) происходит в спокойном воздухе (свободная конвекция) за счёт свободного конвективного теплообмена и излучения. В этом случае при невысоких температурах тела конвективный теплообмен преобладает над лучистым. Поэтому для расчёта такого сложного теплообмена используется уравнение Ньютона – Рихмана: - для конечного процесса за время Q = - для малого отрезка времени d dQ = Здесь Q – количество отданного тепла; F – поверхность теплообмена, м
конвективного теплообмена
t t С другой стороны, при известной массе нагретого тела: M = где V – объём нагретого тела, м То же количество тепла, отдаваемого телом в процессе охлаждения за время d dQ = - c где c – теплоёмкость тела, Дж/ (кг К);
t t
На основе теплового баланса, рассматривая совместно формулы (8.2) и (8.3) с учётом того, что для стенок малой толщины
где m – темп охлаждения (относительная скорость изменения избыточной температуры тела во времени): m = -
Величину темпа охлаждения m в условиях свободной конвекции обычно определяют экспериментальным путём. Если измерения производить в небольшом интервале изменения избыточных температур стенки m = - где моменты времени
(средний температурный напор):
Отношение
Таким образом, при известных конструктивных параметрах тела (V, F) и его теплофизических характеристиках (c, С другой стороны в условиях поставленной задачи суммарный коэффициент теплоотдачи
|

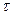 –
–

 , Дж, (8.1)
, Дж, (8.1)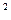 ;
; и коэффициент лучистого теплообмена
и коэффициент лучистого теплообмена  :
: - t
- t 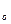 ,
,  С;
С; V, кг,
V, кг,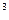 ;
; d
d  – средняя по объёму избыточная температура тела:
– средняя по объёму избыточная температура тела: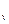 - t
- t 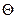 , получаем зависимость
, получаем зависимость

 = c
= c  (8.5)
(8.5) , то темп охлаждения m в этом интервалеможно приближенно считать постоянным и определять его по формуле в конечных разностях:
, то темп охлаждения m в этом интервалеможно приближенно считать постоянным и определять его по формуле в конечных разностях:
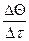 =
= 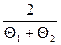
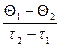 , (8.6)
, (8.6) и
и  – избыточные температуры, измеренные соответственно в
– избыточные температуры, измеренные соответственно в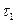 и
и  ;
;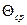 – средняя избыточная температура за промежуток времени
– средняя избыточная температура за промежуток времени 
 ,
, 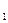 , внутренним диаметром d
, внутренним диаметром d 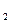 и длиной l данное отношение определяется зависимостью
и длиной l данное отношение определяется зависимостью =
= 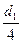
 , м (8.8)
, м (8.8)


