Лабораторная работа № 2. «Исследование устойчивости сжатого стержня»
«Исследование устойчивости сжатого стержня» Введение
При равновесии или движении тел возникают временные дополнительные малые воздействия (возмущения). В зависимости от того, какое состояние принимает тело после исчезновения этого возмущения, говорят, что тело находится в устойчивом или неустойчивом состоянии. Математическую теорию устойчивости создал А.М. Ляпунов, а устойчивость сжатого стержня исследовал Л. Эйлер. Устойчивое, безразличное и неустойчивое равновесие можно представить на примере трех положений равновесия шарика. Поместим шарик на дне лунки, затем немного сместим его и отпустим. Шарик после нескольких колебаний возвратится в исходное состояние. Во втором опыте установим шарик на горизонтальную поверхность, затем немного сместим его. После того как мы отпустим шарик, он останется в последнем положении. Наконец, установим шарик на вершине выпуклой поверхности, затем немного сместим его. Шарик покатится вниз и в начальное положение не вернется. Из опытов следует: первое состояние равновесия - устойчивое, второе - безразличное, третье - неустойчивое. Поэтому, кроме обеспечения прочности и жесткости, следует выполнить расчеты на устойчивость конструкции. Теория
Под устойчивостью понимается свойство системы сохранять свое состояние при внешних воздействиях. Частным случаем является устойчивость первоначальной формы равновесия. Если это свойство не сохраняется, то система становится неустойчивой. Представим следующую идеальную систему. Стержень с постоянным поперечным, сечением, однородный, сжат осевой силой (рис 1). Будем плавно увеличивать силу, добавляя грузы 4, и производить временное нормальное к оси воздействие на стержень силой Рв.
При начальных значениях сжимающей силы, стержень после прекращения бокового воздействия, осуществив несколько колебаний (пунктирные оси), возвращается к прямолинейной форме равновесия. В этом случае потенциальная энергия деформации изгиба больше чем работа сжимающей силы по созданию изгиба стержня. Последующее увеличение сжимающей нагрузки (добавление грузов 4) может привести стержень в такое состояние, когда после бокового временного воздействия силой Рв, стержень не возвращается в исходную прямолинейную форму и остается изогнутым. Это новое равновесное состояние (при отсутствии текучести материала), в отличие от первого (прямолинейного), является более сложным, т.к. кроме напряжений сжатия появились напряжения от изгиба. Между этими двумя положениями существуют промежуточное - критическое, а нагрузка, соответствующая ему, - критическая. Теоретически возможна прямолинейная форма равновесия, но она является неустойчивой и при малейшем возмущении система переходит в новое (криволинейное) равновесное состояние. Л. Эйлер определял критическую силу, как силу способную удержать стержень в слегка изогнутом состоянии, ось которого определяется дифференциальным уравнением
где Е - модуль упругости первого рода,
F - осевая сжимающая сила, у - прогиб стержня.
Решив уравнение (1), получим критическую силу:
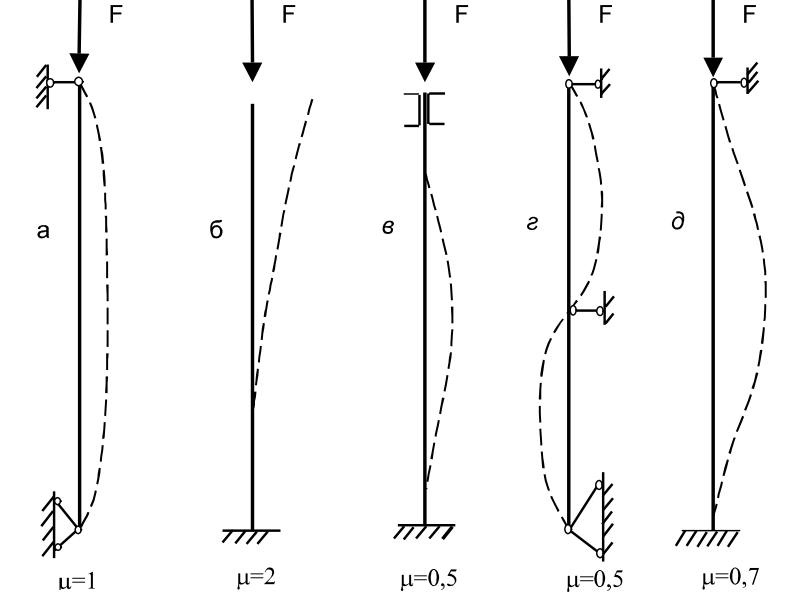
На рис. 2 показаны несколько видов закрепления стержня и соответствующие им значения коэффициента
Рис. 2. Схемы закрепления концов стержня
На основании выше приведенных понятий, определенная опытным путем величина Ркр, отличается от вычисленной по формуле (2). Причина - начальные несовершенства образца для испытаний. Сюда относятся начальная погибь стержня, внецентренное действие силы из-за переменности поперечного сечения по длине стержня и устройства опор, неоднородность материала. Поэтому для определения критической силы FKP опытным путем целесообразно использовать метод Саутвелла, позволяющий существенно снизить влияние начальных несовершенств. Следует иметь ввиду, что в реальных случаях даже при нагрузках меньше критических будем иметь изогнутую форму равновесия стержня. Сущность метода Саутвелла рассмотрим на примере шарнирно закрепленного стержня с начальной погибью (рис. 2а). Опыт показывает, что начальную форму оси изогнутого стержня до нагружения с достаточной точностью можно представить уравнением
Где Z - расстояние сечения до начала координат,
Будем считать, что дополнительные прогибы стержня У1, возникающие от действия сжимающей силы F, также изменяются по его длине по синусоидальному закону
где
У=У0 + У1 (5)
Подставим выражение (5) в уравнение (1), затем разрешив его относительно
С учетом формулы (2) следует
Разделим левую и правую части выражения (7) на
При проведении опыта мы измеряем стрелку прогиба в зависимости от изменения силы F, т.е. получим
Сравнивая выражения (8) и (9), можно сделать вывод, что выражение (8) представляет собой уравнение прямой с угловым коэффициентом
отсекающей на оси ординат отрезок
Эта прямая показана на рис. 3 Из формулы (10) и рис. 3 следует значение критической силы
Аналогичный результат можно получить и при наличии эксцентриситета приложения нагрузки.
|

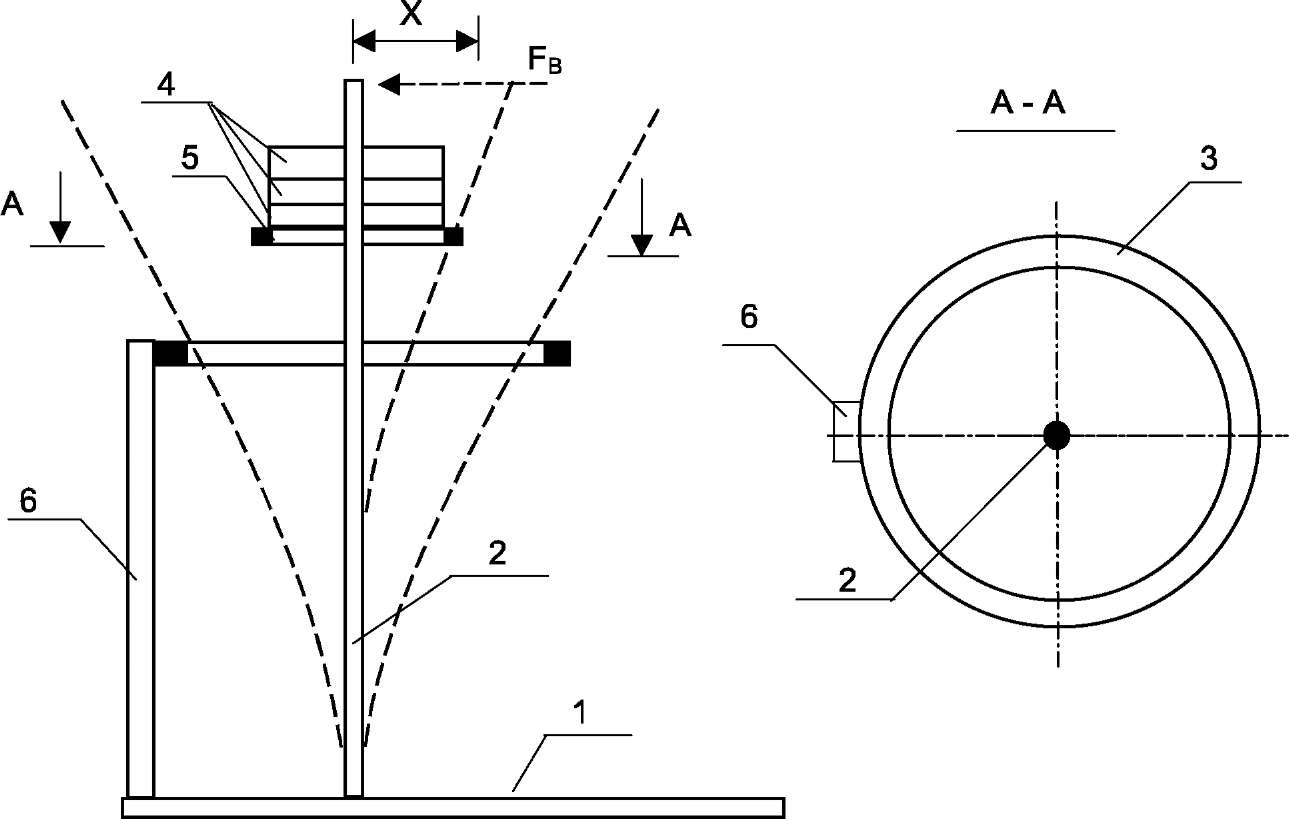 Рис. 1 Моделирование устойчивого и неустойчивого состояния сжатого стержня
1- основание, 2 - испытываемый стержень, 3 - ограничительное кольцо,
4 - грузы, 5 - грузовая площадка, 6 - стойка
Рис. 1 Моделирование устойчивого и неустойчивого состояния сжатого стержня
1- основание, 2 - испытываемый стержень, 3 - ограничительное кольцо,
4 - грузы, 5 - грузовая площадка, 6 - стойка
 (1)
(1) - минимальный момент инерции поперечного сечения,
- минимальный момент инерции поперечного сечения, (2)
(2)
 , (3)
, (3) - начальная стрела прогиба стержня,
- начальная стрела прогиба стержня, - длина стержня.
- длина стержня.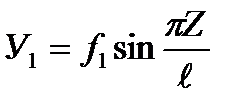 , (4)
, (4) - дополнительная стрела прогиба стержня. Тогда
- дополнительная стрела прогиба стержня. Тогда , (6)
, (6) , (7)
, (7) и преобразуем к виду:
и преобразуем к виду: , (8)
, (8) , (9)
, (9) , (10)
, (10) , (11)
, (11) Рис. 3. График зависимости, определяемой формулой (9)
Рис. 3. График зависимости, определяемой формулой (9)
 , (12)
, (12)


