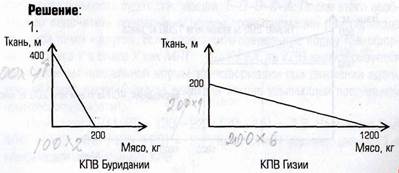
Determining the normal stress
At the plane (simple) pure bend only the bending moments arise at the bar cross section passing through the bar cross section passing through one of the principal axes of the bar cross section. The bending moment is the resultant moment of the internal forces as distributed over the section. To derive the law of the distribution and value of the internal forces arising at the bar cross section the static equations alone are not enough. It is necessary to use the bar deformation condition. If subjecting the bar (specimen) with the network drawn on its surface, the following is detected (Fig. 5.9): 1) The lines 1-1 and 2-2 on the bar surface after deforming will turn at some angle du remaining straight. It is supposed that the bar cross-section being flat before the deformation remains flat after the deformation too (the hypotheses of the plane section). The calculation based on that assumption coordinates with the experience. Since the rectangular network is the same, before and after the deformation the shear stress at the cross section is supposed to be equal to zero. 2) The fiber ab on the convex bar side lengthens, which proves the fact of the fiber tension and the fiber of shortens that proves its compression. The length of the fiber cd doesn’t change that proves the absence of both tension and compression. The bar layer (the fiber cd) under the bending having neither tension nor compression is called the neutral layer. The cross line of the neutral layer with the plane of the bar cross section (Fig. 5.10 a) is called the neutral axis (line). The crossing of the force plane with the cross section plane is called the force line. From the experience results considered it follows that the fiber deforms in different ways: the fiber which is farther from the neutral layer has the larger deformation. Show that the deformation is changed by the line law along the bar section height (Fig. 5.9). Indeed, the length b’b’’ is the total lengthening of the fiber ab whose length before the deformation is the same as the fiber length cd belonging to the neutral layer (see Fig. 5.9). The until strain of this fiber is
where ρ is the radius of the bar neutral layer curvature (the value ρ is unknown); y is the distance from the neutral axis to the fiber considered.
Fig. 5.9. The bar fibers do not press one another i.e. the stresses in the direction perpendicular to the bar axis is equal to zero. Hence, each fiber is subjected to tension or compression. Then, according to Hook’s law for the uniaxial stress we get
i.e. the normal stress change along the height of the bar cross section is proportional to the distance from the neutral axis. There will be the maximum stresses at the upper and lower section edge. The diagram
а) b)
Fig. 5.10.
Having derived the stress distribution law we can also determine the stresses value from the equilibrium equation. Consider the equilibrium of the bar part subjected to the action of the external moment Me and the internal forces, arising at the cross section (Fig. 5.10 b). Under the equilibrium of this bar part six equations of the equilibrium have to be kept: the projection sum of the acting force on three coordinate axes, three moment sums about x, y, z - axes being equal to zero. 1. Equate to zero the projection sum on y-axis: 2. The same for x-axis: 3. Equate to zero the projection sum on the z -axis:
We get But Hence,
This integral represents the first moment of the bar cross-section area about the neutral axis. It is equal to zero, hence, the neutral axis under bending passes through the centroid of the cross section. 4. The equation 5. The equation But 6. Equate to zero the moments sum of the forces with respect to the x -axis:
Using the formula (5.11) we get
The integral Jx is the second moment of the section area about the neutral x -axis. Some external moments as well as any other load can influence on the bar cut part. In this case the equilibrium equation
from this
The value It was shown above that the neutral line of the cross section passes through the centroid. Hence, the bar axis (longitudinal axis) being the geometric place of the cross section centroid is located on the neutral layer. In this way we get the expression (5.13) determining the curvature of the bar axis. So, the bar axis curvature under bending is proportional to the bending moment and inversally proportional to the value EIx called the flexural rigidity. Substituting the value
allowing us to determine the normal stress at any point of the bar cross-section. The formula (5.14) is derived for the pure bending. Under the cross bending there arise both normal and shearing stresses at the bar cross-section. The appearance of shearing stresses is accompanied by appearance of the shearing strain and as a result the bar cross sections are no longer plane i.e. pressing fibers against each other takes place there. The more detailed analysis shows that the formula (5.14) gives quite reliable results also under the cross bending.
|

 (5.10)
(5.10)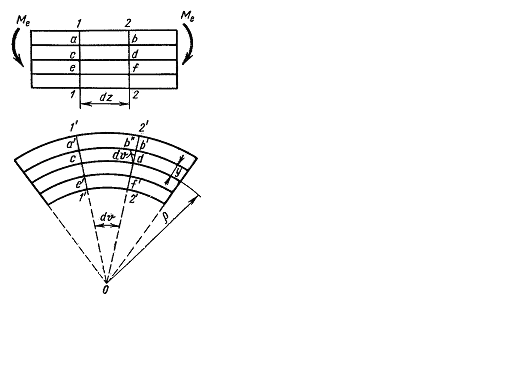
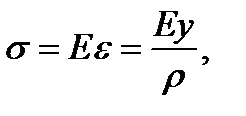 (5.11)
(5.11) is shown in Fig. 5.10 a. We shall consider the tension stress as positive.
is shown in Fig. 5.10 a. We shall consider the tension stress as positive.

 But
But 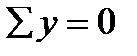 and
and  turn into identities because the internal forces σ dA are perpendicular to these axes.
turn into identities because the internal forces σ dA are perpendicular to these axes. or
or 

 as soon as
as soon as  the bend bar is to be considered.
the bend bar is to be considered.
 turns into an identity because the internal stresses σ dA are parallel to z -axis.
turns into an identity because the internal stresses σ dA are parallel to z -axis.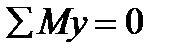 gives
gives 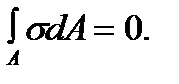 Using the formula (5.11) we get
Using the formula (5.11) we get 
 hence,
hence, 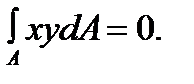 The integral
The integral  is the product of the inertia cross section with respect to the x and y -axes. As soon as it is equal to zero, the x and y -axes are to be the principal axes of the section and the moment Me has to lie on the plane passing through one of the principal axes, which is fulfilled under the plane bending. From this condition it also follows that the force line and the neutral axis are mutually perpendicular.
is the product of the inertia cross section with respect to the x and y -axes. As soon as it is equal to zero, the x and y -axes are to be the principal axes of the section and the moment Me has to lie on the plane passing through one of the principal axes, which is fulfilled under the plane bending. From this condition it also follows that the force line and the neutral axis are mutually perpendicular.
 and
and 
 contains the algebraic moments sum of all the forces and it is equal to the bending moment at the cross section M. The above said remembered relation will be presented by
contains the algebraic moments sum of all the forces and it is equal to the bending moment at the cross section M. The above said remembered relation will be presented by (5.12)
(5.12) (5.13)
(5.13)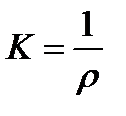 is the curvature of the bar neutral layer.
is the curvature of the bar neutral layer. found into (5.11) we get the important formula
found into (5.11) we get the important formula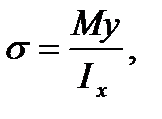 (5.14)
(5.14)