The purpose of strength hypotheses

 

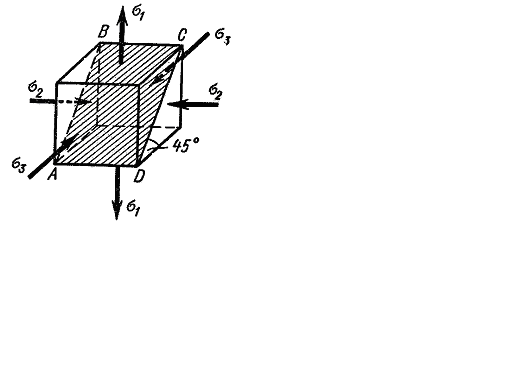
Up to now there have been studied the stress analyses for the cases when the material is in the uniaxial stress tension, compression or the simplest biaxial one, when the principal stresses at each point are equal to each other by the value and opposite by the sign (shear, torsion).

The composition of the strength conditions has not caused difficulties in these cases. To provide the material strength it was required that the maximum normal stress (in tension, compression) or the maximum shearing stress (in torsion) should not surpass the corresponding allowable working stress whose value was established experimentally by the received corresponding yield stress or the tensile strength (for brittle materials).

The general case of the triaxial stress state is represented in Fig. 6.1. The action plane of the maximum shearing stress is also shown in the figure. Remember that the following rule of the principal stress designation was accepted earlier: (with the sign consideration).

The question arises: what are the stress values () so that the limit state of a material can take place, i.e. its failure or peasfic deformations take place.

Answering this question it would be necessary to solve another problem: how to determine the safe (allowable) values of the principal stresses .

The problem set is extremely difficult. The most reliable way of its solving would be to test the specimen under a given correlation of the principal stresses up to the failure or the yield beginning and thus to determine the limit principal stresses and then their allowable values.

However this way has to be refused as every new combination would require a new test.

Besides, these tests require very complicated machines and devices. Therefore it is necessary to have some hypothesis (theory) which would allow to appreciate the danger of passing a material in the limit state under the combined stress state, not resorting each time to the labor-consuming tests but using only the given simplest tests, i.e. the tests for the uniaxial stress.

Thus, the hypothesis construction is based on the assumption that any two stress states are considered as equally dangerous and equally strengthened, should they become with the proportional increasing of the principal stresses in the same number oftimes simultaneously.

 

 

 

 

Fig. 6.1.

 

In this case the factor of safety for two stress status under the given conditions will be equal.