The energy hypotheses of strength
In accordance with the first of the energy hypothesis the material strength in the combined stress state is ensured if the specific potential energy of deformation is lesser than the allowable specific potential energy accepted for the uniaxial stress:
The specific potential energy of deformations in the general state of stress is equal to
This value is always positive. Therefore the energy hypothesis like the third one does not consider the difference between tension and compression, in other words, using this hypothesis one has to accept
The allowable specific potential energy in the uniaxial stress is determined by the formula under
Substituting the values u and uadm into (6.5) we get
or
The experiments show that better results are obtained if to accept not the entire deformation energy but only that part of it which is connected with the change of the body shape as criterion. Hence, the strength condition according to the energy hypothesis due to distortion (it is also called the forth hypothesis too) has the form:
In a particular case for the plane stress state
|

 (6.5)
(6.5) (6.6)
(6.6) (6.7)
(6.7)
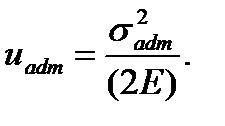 (6.8)
(6.8)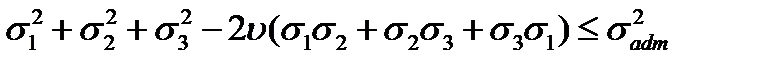
 (6.9)
(6.9) (6.10)
(6.10)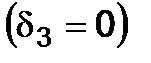 we get
we get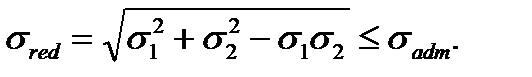 (6.11)
(6.11)