Strength conditions with normal stresses

To ensure the bar strength it is necessary that the maximum tension and maximum compression stresses under bending in a dangerous section, i.e. in the section where M has the maximum value, should not surpass the corresponding allowable working stress (only bars with the constant section along the length are considered).

Denote (Fig. 5.10 b) by the distance from the neutral axis to the most remote tension fiber, by h_c the distance to the most compressed fiber. Then the most tension stress under bending is

 

(5.15)

 

the most compression stress (with an absolute value) is

(5.16)

The allowable working stresses in tension and compression are different for brittle materials. Therefore for the beams made of these materials the sections are usually applied which are asymmetrical with respect to the neutral axis. So the section then is located that h_t < h_c. In this case two conditions for the strength are to be composed:

with the maximum tension stresses

 

(5.17)

 

with the maximum compression stresses

(5.18)

 

where are the section modulus of the tension and compression fibers.

If the bar section is symmetrical about the neutral axis, we get the formula

(5.19)

 

Defining we get the following condition of the strength under the same allowable working stresses in tension and compression

(5.20)

 

The value is called the section modulus under bending.

Example. Determine the beam section of the double -T profile in the length L=6 m loaded by the uniformly distributed load

Solving. For this case the maximum bending moment takes place in the middle beam section:

 

 

The required section modulus is

 

 

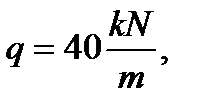
Select the double -T profile of № 45 from the tables of sections which has (W_x understressing being < 5%, which is allowable).