The second and third strength hypotheses
In accordance with the second hypothesis of the strength also called the maximum linear deformation hypothesis, the maximum linear deformation is accepted as the strength criterion. Since the experiments do not verify this theory, we shall not explain it in detail and pass on to describing the third hypothesis, widely used nowadays. In accordance with the third strength hypothesis also called the maximum shearing stress hypothesis: the material strength in the combined stress state is ensured if the maximum shearing stress is lesser than the shearing allowable working stress accepted for the uniaxial stress, i.e.
The maximum shearing stress in the biaxial stress state occurs on the second at the angle For the general state of stress the maximum shearing stress occurs on the ABCD plane (see Fig. 6.1):
The shearing allowable working stress Using the formula (6.3) we get
The expression implies some stress called the reduced or equivalent (rated) stress. It must be understood as the stress which is to be established in the specimen in tension (or compression) so that its tensed strength was equal to the specimen strength being in the conditions of the combined stress state.
|
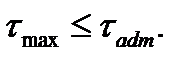(6.2)
to the principal stress direction and is equal to half the difference of these stresses.
(6.3)
in the uniaxial stress is connected with the normal allowable working stress 
by the relation 
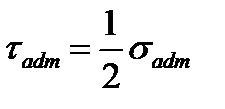followed from the previous formula, if 
is equal to zero in it.
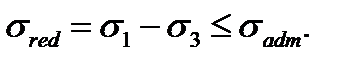(6.4)
