ЭВРИСТИЧЕСКИЕ МЕТОДЫ ПОИСКА РЕШЕНИЙ
Во многих случаях ввиду практической сложности решения в точной форме, наряду с другими методами можно использовать алгоритмы, которые называют эвристическими. Их преимуществом является значительное упрощение принятия решения в условиях неопределенности. Недостаток заключается в том, что невозможно узнать, как близко от оптимального найденное решение. Эвристических методов принятия решения много. Рассмотрим кратко некоторые из них. Конструктивные методы. Суть метода состоит в постепенном приближении к решению путем добавления к нему отдельных компонентов до того момента, пока не получится выполнимое решение. Метод декомпозиции. Задачу подразделяют на подзадачи, считая выход одной задачи в качестве входа другой. Манипулирование с моделью. Меняют структуру модели с целью получения решения. Для этого используют различные приемы, в частности уменьшают пространство состояний (линеаризация функций, группировка переменных и т.д.). Методы локального улучшения. Основываются на поиске решения среди элементов некоторой окрестности, не думая о наличии глобального (лучшего) решения. Эвристический поиск. Методом проб и ошибок выбирается цепочка выводов, ведущая к цели. При неуспехе осуществляется возврат для поиска других цепочек выводов. Табу поиска решения (ТП). Направляет локальную процедуру эвристического поиска за пределы локального оптимума. ТП следует из предположения, что плохой стратегический выбор может нести больше информации, чем хороший случайный выбор. Начинается поиск как простой локальный поиск, пока не выполнится определенный критерий. Затем окрестность поиска модифицируется. Каждый раз на очередное решение накладывается запрет (табу) с целью расширения вариантов (проверка новых идей). Генетический алгоритм. Это управляющая программная структура, которая выполняет последовательность преобразований и операций, предназначенных для моделирования процесса эволюции совокупности кодовых строк методами естественной эволюции. Для этого из совокупности строк по установленным признакам отбираются две строки – хромосомы. После некоторой операции смешивания (скрещивания) получают две новые строки – потомки. Их оценивают по определенным критериям и скрещивают с другими строками с целью получения новых или закрепления нужных свойств. Будучи разновидностью методов поиска с элементами случайности, генетические алгоритмы имеют целью нахождение приемлемого, а не оптимального решения задачи. Это связано с тем, что для сложной системы часто требуется найти хоть какое-нибудь удовлетворительное решение, а проблема достижения оптимума отходит на второй план. При этом методы, ориентированные на поиск именно оптимального решения, вследствие чрезвычайной сложности задачи становятся вообще неприменимыми. Основные отличия генетических алгоритмов следующие. Во-первых, эти алгоритмы работают с кодами, в которых представлен набор параметров, напрямую зависящих от аргументов целевой функции. В процессе манипуляции с кодами независимо от их интерпретации они рассматриваются просто как битовые строки. Во-вторых, для поиска генетический алгоритм использует несколько точек поискового пространства одновременно, а не переходит от точки к точке. Это позволяет преодолеть опасность попадания в локальный экстремум целевой функции, если она не является унимодальной (одноэкстремальной). В-третьих, генетический алгоритм в процессе работы не использует никакой дополнительной информации, кроме области допустимых значений параметров и целевой функции в произвольной точке. В-четвертых, генетические алгоритмы одновременно используют как вероятностные правила для порождения новых точек анализа, так и детерминированные правила перехода от одних точек к другим. Сам код и его структура описываются понятием генотип, а его смысловая интерпретация, с точки зрения решаемой задачи, - понятием фенотип. Код представляет точку пространства поиска. Совокупность точек является набором кодов (хромосомы или особи) или популяцией. Размер популяции представляет собой одну из характеристик генетического алгоритма. Смена популяций идентифицируется номером (поколением). Генерация новых особей (размножение) идет от родителей к потомкам с помощью оператора скрещивания – кроссинговера. Вероятность применения оператора скрещивания также является одним из параметров алгоритма. Выбор пар родителей производит оператор отбора. Моделирование процесса мутации новых особей осуществляется за счет оператора мутации. Ему также соответствует некоторая вероятность. Поскольку размер популяции фиксирован, то порождение потомков должно сопровождаться уничтожением других особей. Выбор особей для уничтожения осуществляет оператор редукции. Основным параметром работы операторов отбора и редукции является качество особи, которое определяется значением целевой функции в данной точке пространства поиска. Критериями останова генетического алгоритма являются следующие события: - сформировано заданное пользователем число поколений, - популяция достигла заданного пользователем качества, - скорость улучшения популяций упала ниже заданного порога (достигнут некоторый уровень сходимости или подобия особей). На рис. 4.1 дана блок-схема генетического алгоритма. В основе оператора отбора лежит принцип «выживает сильнейший». Например, вероятность участия в процессе размножения может быть вычислена как
где n - размер популяции, Аналогично может быть решен вопрос уничтожения особей (с учетом обратной зависимости вероятности уничтожения от качества особи). Рассмотрим простейший оператор скрещивания следующих строк: X1X2…Xn; Y1Y2…Yn. На первом этапе равновероятно выбирается натуральное число k от 1 до n-1. Это число называется точкой разбиения. В соответствии с ним обе исходные строки разбиваются на две подстроки: X1X2…XkXk+1…Xn; Y1Y2…YkYk+1…Yn. На втором этапе строки обмениваются своими подстроками, лежащими после точки разбиения, то есть элементами с k+1 по n-ный. Так получаются две новых строки, которые наследуют частично свойства обоих родителей: X1X2…XkYk+1…Yn; Y1Y2…YkXk+1…Xn. Иногда применяется особая стратегия элитизма, которая предполагает переход в следующее поколение элиты (лучших особей) без всяких изменений. Количество элитных особей можно вычислить, например, по формуле K=(1-P)N,
где Р – вероятность применения оператора скрещивания, N – размер популяции. Вероятность мутации в отличие от скрещивания выбирается достаточно малой. Процесс мутации заключается в замене одного из элементов строки на другое значение (перестановка, смена, инверсия и т. д.). Поскольку генетические операторы применяются к популяциям неоднократно, качество особей растет и в итоге в том или ином объеме достигается требуемая цель. Рассмотрим следующий очевидный пример. Пусть имеется набор чисел от 0 до 31 и функция, определенная на этом наборе f(x)=x. Требуется найти максимальное значение функции 31. В качестве фенотипа используем двоичное представление аргументов. Генотип – строка из 5 бит. Целевой функцией будет сама рассматриваемая функция, аргументом которой является число, чье двоичное представление использует алгоритм. Определим характеристики генетического алгоритма: размер популяции 4, вероятность мутации 0.001, мутация – инверсия одного из битов, выбираемого случайно по равномерному закону. Операторы скрещивания и отбора аналогичны вышеизложенным. Элитизм не используется. На основе равномерного распределения создадим исходную популяцию – табл. 4.1. Исходная популяция Таблица 4.1
Пусть оператор отбора выбрал для производства потомков две пары строк (1, 2) и (3, 4). Работа оператора скрещивания иллюстрирована табл. 4.2 (разбиение на подстроки – независимое).
Работа оператора скрещивания Таблица 4.2
Пусть оператор мутации сработал для младшего бита в строке 3 и данный код стал 10001. Таким образом, популяция за счет порожденных потомков расширилась до восьми особей – табл. 4.3.
Работа оператора мутации Таблица 4.3
Оператор редукции далее сократит популяцию до исходного числа особей, исключив из нее те, чье значение целевой функции минимально. Исключены будут строки 1, 3, 4 и 5. Получим табл. 4.4. Уже на этом шаге работы генетического алгоритма видны его положительные результаты. Если первоначально среднее значение целевой функции было 10.75, а ее минимальное значение составляло 2, то в первом же поколении среднее значение выросло до 19, а минимальное значение – до 14.
Работа оператора редукции Таблица 4.4
Рассмотрим более сложный пример. Пусть дано множество из 5-ти городов и матрица расстояний между ними (или стоимость переезда). Цель – объехать все города по кратчайшему пути (или с минимальными затратами). При этом в каждом городе останавливаться можно один раз и закончить путь надо в том же городе, из которого начался маршрут. Матрица стоимости проезда имеет вид: 0 4 6 2 9 4 0 3 2 9 6 3 0 5 9 2 2 5 0 8 9 9 9 8 0 Решение представим в виде перестановки чисел от 1 до 5, отображающей последовательность посещения городов. Значение целевой функции будет равно стоимости всей поездки (одним из оптимальных решений является маршрут 514235 стоимостью 25). Оператор отбора аналогичен тому, который использовался в предыдущем примере. В качестве оператора скрещивания выберем процедуру двухточечного скрещивания. Например, пусть есть две родительские перестановки: 12345 и 34521. Случайно и равновероятно выбираются две точки разрыва. Для примера возьмем ситуацию, когда первая точка разрыва находится между первым и вторым элементами перестановки, а вторая – между четвертым и пятым: 1½ 234½ 5, 3½ 452½ 1. На первом этапе перестановки обмениваются фрагментами, заключенными между точками разрыва (452, 234) с потерей остальных чисел (вместо них поставим звездочки): *½ 452½ *, *½ 234½ *. На втором этапе – звездочки заменяются числами из исходной родительской перестановки, начиная со второго числа фрагмента и пропуская уже имеющиеся в новой перестановке числа. В данном случае в исходной перестановке 1½ 234½ 5 начальным числом является 3. После его подстановки в *½ 452½ * на место первой звездочки получим 3½ 452½ *, где уже есть числа 4, 5, стоящие после 3 в исходной последовательности 1½ 234½ 5. Пропускаем их и переходим к началу исходной последовательности: число 1 можно использовать для обмена, так как его нет в новой перестановке 3½ 452½ *. Получаем вместо исходной последовательности 12345 ряд 34521. Также из 3½ 452½ 1 и *½ 234½ * получаем последовательно: 5½ 234½ * и 52341. Оператор мутации будет представлять собой случайную перестановку двух чисел в хромосоме, также выбранных случайно по равномерному закону. Вероятность мутации 0.01. Размер популяции выберем равным 4. Исходная популяция представлена в таблице 4.5 (f(x) учитывает поездку из последнего города в первый).
Исходная популяция Таблица 4.5
Пусть для скрещивания были выбраны следующие пары: 1, 3 и 2, 4. В результате были получены потомки, представленные в табл. 4.6.
Работа оператора скрещивания Таблица 4.6
Пусть для потомка 12354 сработал оператор мутации и обменялись местами числа 2 и 3. В данном случае строка 12354 изменилась и приняла значение 13254. Популяция первого поколения после отсечения худших особей в результате работы оператора редукции приняла вид, представленный в табл. 4.7. Работа оператора редукции Таблица 4.7
Пусть для получения второго поколения были выбраны следующие пары строк: 1, 4 и 2, 3. И в результате были получены потомки, показанные в табл. 4.8. Работа оператора скрещивания Таблица 4.8
Популяция второго поколения после отсечения худших особей приняла вид, показанный в табл.4.9. Работа оператора редукции Таблица 4.9
Таким образом, после двух итераций значение целевой функции для лучшего решения изменилось с 29 на 28, среднее значение изменилось с 30.5 на 28.75, а общее количество - с 122 на 115. Налицо улучшение популяции. Одной из основных областей применения генетических алгоритмов является обучение нейронных сетей. Для этого создается набор примеров, который представляет собой совокупность векторов, характеризующих значения всех входов и выходов нейронной сети. Цель обучения нейронной сети заключается в подборе значений всех ее характеристик таким образом, чтобы отличия выходов от эталонных не превышали заранее установленной величины. Таким образом, задача обучения нейронной сети сводится к задаче поиска приемлемого решения. Генетические алгоритмы эффективны при улучшении сетей, уже созданных и обученных с помощью какого-либо другого алгоритма. Для иллюстрации рассмотрим пример сети прямого распространения, показанной на рис. 4.2. Сеть состоит из 6 нейронов: трех входных, двух скрытых и одного выходного. В качестве функции активации всех скрытых и выходного нейронов используется сигмодальная функция: F(Sym) = 1/(1+e-PSum), Sum = где n – количество входов нейрона; xi – значение на i-м входе; wi – вес i-го входа; P- параметр функции активации, влияющей на ее крутизну (чем больше P, тем ближе сигмодальная функция приближается к пороговой). Таким образом, векторы примеров будут иметь вид (х1, х2, х3, y1), где xi
– входные значения, а y1 – эталонное выходное значение. Для вычисления значения целевой функции будем использовать формулу С = где k – количество примеров; Таким образом, целевая функция будет представлять собой максимальное для набора примеров относительное отклонение от эталонного значения, выраженное в процентах. Чем меньше значение целевой функции, тем сеть лучше. Работу алгоритма можно остановить, если для одной из особей значение целевой функции будет равно, например, 0.1. Критерием останова может быть также число поколений. Для обучения нейронной сети размер популяции выбирается достаточно большим, например 100. Хромосома в рассматриваемом случае будет представлять массив из 11 действительных чисел, по четыре на каждый скрытый нейрон и три для выходного нейрона, которые представляют собой веса соответствующих входов нейронов и параметры их функций активации:
Для элементов хромосомы – генов – введем ограничения, обусловленные природой нейросетей: -1 £ wij £ 1 и Pi > 0. В качестве операторов скрещивания, отбора и редукции выберем традиционные операторы, рассмотренные выше при решении задачи нахождения максимума одномерной функции. Дополнительно для оператора скрещивания можно установить вероятность применения 0.95 и использовать элитизм. В качестве оператора мутации будем использовать случайное изменение значений весов и параметра функции активации для каждого нейрона на случайную величину. Вероятность мутации 0.01. Причем одновременно будет изменяться параметр функции только для одного нейрона, и для каждого нейрона будет изменяться один из входных весов. Какие конкретно веса и параметры будут меняться, определяется по равномерному закону. Например, мутация может быть следующей: значение P2 увеличивается на 0.1; значение w13 уменьшается на 0.05; w21 – уменьшается на 0.01; w31 – увеличивается на 0.05. Исходная популяция будет формироваться на основе равномерного распределения для каждого элемента хромосомы. Целью работы генетического алгоритма будет поиск значений весов для всех скрытых и выходных нейронов, а также параметра P их функции активации. После останова работы такого алгоритма мы получим обученную нейросеть, удовлетворяющую заданным требованиям по w и P. Полное построение нейросети с изменением ее структуры решается обычно в два этапа, на каждом из которых используется свой генетический алгоритм. На первом этапе вычисляются базовые характеристики: числа скрытых слоев и нейронов в каждом слое. При этом оценка качества каждого решения ведется, например, в течение 100 поколений, после чего выбирается лучшая особь. На втором этапе проводится оптимизация матрицы весов и функции активации, как было рассмотрено выше. На обоих этапах используется один и тот же набор обучающих примеров, являющийся единственной информацией, использующейся в качестве исходных данных для построения и обучения нейронной сети. Основным способом повышения скорости работы генетических алгоритмов является распараллеливание. При этом используется особенность генетических алгоритмов, заключающаяся в многократном вычислении значений целевой функции для каждой особи, применении операторов скрещивания и мутаций для нескольких родительских пар и т. д. Все эти процессы могут быть реализованы на параллельных вычислительных системах. Достаточно продуктивным средством повышения эффективности генетического алгоритма является его адаптация в процессе поиска, когда меняются вероятности генетических операторов, стратегии выбора, количества популяций и другие параметры.
|


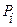 =
=  /
/ 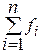 ,
, - номер особи,
- номер особи, 
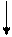

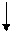

 xiwi ,
xiwi ,
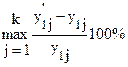 ,
,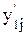 – значение выхода нейронной сети для j-го примера; y1j- эталонное значение выхода нейронной сети для j-го примера.
– значение выхода нейронной сети для j-го примера; y1j- эталонное значение выхода нейронной сети для j-го примера.


