ПРОБЛЕМА Распознавания образов
Распознавание образов является классической задачей ИИ, задачей аппаратно-программного интерфейса ИИС или самостоятельной задачей интеллектуальных информационных систем идентификации и наблюдения. В целом проблема распознавания образов (слуховых, зрительных и т.д.) состоит из двух частей: обучения и распознавания. Обучение осуществляется путем показа отдельных объектов с указанием их принадлежности тому или иному образу. В результате обучения распознающая система должна приобрести способность одинаково реагировать на все объекты одного образца и различно – на все объекты различных образцов. Одной из центральных задач распознавания является выбор исходного описания объекта. Здесь можно отметить геометрические и структурные подходы. Геометрический подход основывается на различии формы объектов. Чем компактнее сами объекты и чем дальше они расположены друг от друга, тем легче идет процесс обучения и распознавания. Структурный подход основан на анализе элементов объекта, поэтому его называют лингвистическим. При этом сначала выделяют фрагменты всех объектов и характеристики их взаимного расположения. Все это образует исходную БД - словарь, позволяющий строить различные логические конструкции-предположения. Из них отбираются наиболее существенные для данного конкретного случая. Далее строится описание единого образа объектов, который используется затем для идентификации других объектов, подпадающих или нет под данный образ. Наилучшим средством решения проблемы распознавания являются нейронные сети, поскольку они априори призваны имитировать творческие процессы мышления биологических систем. Примером задач распознавания является распознавание 26 символов латинского алфавита. В качестве датчика предполагается система, которая выполняет оцифровку каждого символа, находящегося в стандартном поле шаблона размером 5´ 7. Например, символ A может быть представлен рис. 5.1, а и б [11, с.199].
Проектируемая нейронная сеть должна точно распознавать 26 идеальных векторов, каждый из которых содержит 35 элементов, и с максимальной точностью воспроизводить зашумленные векторы. Соответственно на вход нейросети поступает вектор с 35 элементами; вектор выхода содержит 26 элементов, только один из которых равен 1, а остальные – 0. Таким образом, нейронная сеть имеет 35 входов и 26 нейронов в выходном слое. Для решения задачи достаточно выбрать двухслойную сеть с логарифмическими сигмодальными функциями активации в каждом слое. Структурная схема такой сети в обозначениях пакета МАТЛАБ показана на рис. 5.2.
Cкрытый слой имеет 10 нейронов (можно больше). Помехи приводят к тому, что сеть не будет формировать вектор выхода, состоящий только из единиц и нулей. Поэтому по завершении этапа обучения нейросеть следует оснастить блоком М-функции compet обработки выходных сигналов для присваивания значения 1 только одному элементу вектора выхода. Обучение необходимо проводить как с идеальными, так и с зашумленными входными векторами, чередуя их для закрепления свойств распознавания символов. Уровень допустимых помех (размытость оцифрованных элементов поля шаблона) определяется требуемой вероятностью правильного опознания. Шаблон для рассматриваемого символа A можно получить с помощью таких МАТЛАБ-операторов: [alphabet, targets] = prprob; i = 2; ti = alphabet(:, i); letter{i} = reshape(ti, 5, 7)’; letter{i} что дает: ans = 0 0 1 0 0 0 1 0 1 0 0 1 0 1 0 1 0 0 0 1 1 1 1 1 1 1 0 0 0 1 1 0 0 0 1 Для инициализации сети вызывается М-файл prprob, который формирует массив векторов входа alphabet размера 35´ 26 с шаблонами символов алфавита и массив целевых векторов targets: [alphabet, targets] = prprob; [R, Q] = size(alphabet); [S2, Q] = size(targets); Двухслойная нейронная сеть создается с помощью команды newff: S1 = 10; net = newff (minmax (alphabet), [S1 S2], {‘logsig’ ‘logsig’}, ‘traingdx’); net.LW{2, 1} = net.LW{2, 1}*0.01; net.b{2} = net.b{2}*0.01;
Структура сети вызывается оператором gensim(net) – рис.5.3.
Структура блока Neural Network показана на рис.5.4:
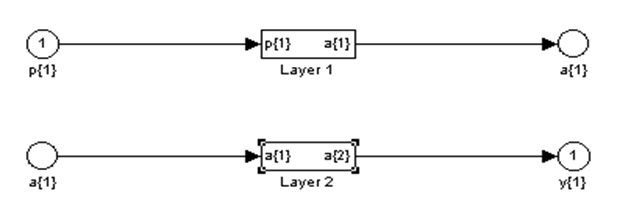
Структура блоков Lauer 1 и Lauer 2 представлена на рис. 5.5, 5.6. Первоначально сеть обучается в отсутствии шума с максимальным числом циклов обучения 5000 либо до достижения допустимой средней квадратичной погрешности, равной 0.1 (рис. 5.7): P = alphabet; T = targets; net.performFcn = ‘sse’; net.trainParam.goal = 0.1; net.trainParam.show = 20; net.trainParam.epochs = 5000; net.trainParam.mc = 0.95; [net, tr] = train(net, P, T); % Рис.5.7
Обучение нейронной сети, малочувствительной к помехам, проведем с применением двух идеальных и двух зашумленных копий векторов алфавита. Целевые векторы состоят из четырех копий. Зашумленные векторы имеют шум со средним значением 0.1 и 0.2. Это позволит сети правильно распознавать зашумленные символы и в то же время хорошо распознавать идеальные векторы. При обучении с шумом максимальное число циклов обучения сократим до 300, а допустимую погрешность увеличим до 0.6 (рис.5.8): netn = net; netn.trainParam.goal = 0.6; netn.trainParam.epochs = 300; T = [targets targets targets targets]; for pass = 1: 10 P = [alphabet, alphabet, … (alphabet + randn(R, Q)*0.1), … (alphabet + randn(R, Q)*0.2)]; [netn, tr] = train(netn, P, T); end % Рис.5.8 Поскольку сеть обучалась в присутствии шума, имеет смысл повторить ее обучение без шумов, чтобы гарантировать, что идеальные векторы входа классифицируются правильно:

netn.trainParam.goal = 0.1; % Предельная среднеквадратичная погрешность netn.trainParam.epochs = 500; % Максимальное количество циклов обучения net.trainParam.show = 5; % Частота вывода результатов на экран [netn, tr] = train(netn, P, T);
Эффективность нейронной сети будем оценивать следующим образом. Рассмотрим две структуры нейронной сети: сеть 1, обученную на идеальных последовательностях, и сеть 2, обученную на зашумленных последовательностях. Проверка функционирования производится на 100 векторах входа при различных уровнях шума. Тестирование реализуем следующим образом. Шум со средним значением 0 и стандартным отклонением от 0 до 0.5 с шагом 0.05 добавляется к векторам входа. Для каждого уровня шума формируется 100 последовательностей для каждого символа и вычисляется выход сети. Выходной сигнал обрабатывается М-функцией compet с той целью, чтобы выбрать только один из 26 элементов вектора выхода. После этого оценивается количество ошибочных классификаций и вычисляется процент ошибки. Ниже приведен сценарий appcr1, который выполняет эти операции: noise_range = 0:.05:.5; max_test = 100; network1 = [ ]; network2 = [ ]; T = targets;
% выполнить тест for noiselevel = noise_range errors1 = 0; errors2 = 0;
for i=1: max_test P = alphabet + randn(35, 26)*noiselevel;
% Тест для сети 1 A = sim(net, P); AA = compet(A); errors1 = errors1 + sum(sum(abs(AA-T)))/2;
% Тест для сети 2 An = sim(netn, P); AAn = compet(An); errors2 = errors2 + sum(sum(abs(AAn-T)))/2; echo off end
% Средние значения ошибок (100 последовательностей из 26 векторов целей) network1 = [network1 errors1/26/100]; network2 = [network2 errors2/26/100]; end
График погрешностей сети от уровня входного шума формируется так: plot(noise_range, network1*100, ‘- -‘, noise_range, network2*100);
Погрешности сети 2, обученной на зашумленных векторах, при шуме со среднеквадратичным значением 0.2 оказываются на 3.5% ниже, чем для сети, обученной на идеальных входных последовательностях. Дальнейшее повышение точности требует увеличения количества нейронов в скрытом слое.
|