Применение нечетких множеств в ЭС рассмотрим на примере сортировщика изделий на поточной линии. Работа сортировщика сводится к оценке качества изделия на основе поступающей информации и определения угла поворота манипулятора для пересылки изделия в нужном направлении – на сборку, в брак или на доработку.
В качестве измеряемых входных параметров при определении качества изделия используются:  - кривизна после резки и шлифования,
- кривизна после резки и шлифования,  - температура после обжига и охлаждения.
- температура после обжига и охлаждения.  Î [
Î [  ,
, 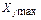 ],
],  =
=  , где [
, где [  ,
, 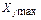 ] означает диапазон возможных значений
] означает диапазон возможных значений  . Параметры
. Параметры  ,
,  рассматриваются как нечеткие множества, формирующие лингвистические переменные, описываемые тройками
рассматриваются как нечеткие множества, формирующие лингвистические переменные, описываемые тройками  ={<
={<  ,
,  ,
,  > },
> },  Î
Î  (
( ),
),  =
=  ,
,  =
=  , где
, где  (
( ) – расширенное терм-множество (значение) лингвистической переменной “ПАРАМЕТР”,
) – расширенное терм-множество (значение) лингвистической переменной “ПАРАМЕТР”,  - нечеткое множество, описываемое функцией принадлежности
- нечеткое множество, описываемое функцией принадлежности  , принимающей значения в интервале [0, 1] для всех
, принимающей значения в интервале [0, 1] для всех  из универсумов
из универсумов  = {0, 1, …, 10} (записывается как
= {0, 1, …, 10} (записывается как  :
:  ®[0, 1]). Значения переменной “ПАРАМЕТР” приведены в табл. 10.3.
®[0, 1]). Значения переменной “ПАРАМЕТР” приведены в табл. 10.3.
Таблица 10.3. Значения переменной " ПАРАМЕТР"
| Значения переменной “ПАРАМЕТР”
|  Î Î 
|
| Несущественное
|
|
| Почти малое
|
|
| Малое
|
|
| Чуть больше, чем малое
|
|
| Почти среднее
|
|
| Среднее
|
|
| Чуть более, чем среднее
|
|
| Почти большое
|
|
| Большое
|
|
| Чуть более, чем большое
|
|
| Предельное
|
|
Так как  - промышленный параметр, а
- промышленный параметр, а  - нормированное множество, то для отображения
- нормированное множество, то для отображения  ®
®  предлагается очевидная формула:
предлагается очевидная формула:
 =
=  [(
[( (
( )-1)
)-1)  ], (10.1)
], (10.1)
где  - входящий,
- входящий,  - мощность,
- мощность,  ³ 1.
³ 1.
Ранее было
 =
=  (
( )/
)/  . (10.2)
. (10.2)
Для вычисления синглтонов  (
( )/
)/  предлагается экспертное выражение
предлагается экспертное выражение
 (
( ) =1-
) =1-  ê
ê  -
-
-  [(
[( (
( )-1)
)-1)  ], (10.3)
], (10.3)
где

- значение

из таблицы 10.3. Пример:

=1;

,

такие, что для каждого по (10.1)

=0 (

=0 в табл.10.3 соответствует значение переменной ПАРАМЕТР
=несущественное). Тогда из (10.3), табл.10.3, (10.3) и (10.2) имеем:

=

=
несущественное = 1/0+0.9/1+0.8/2+0.7/3+
+0.6/4+0.5/5+0.4/6+0.3/7+0.2/8+0.1/9+0/10.
Выходной параметр также представлен в виде нечеткого множества качества изделия  , формирующего лингвистическую переменную ”КАЧЕСТВО1”, описываемого тройками вида
, формирующего лингвистическую переменную ”КАЧЕСТВО1”, описываемого тройками вида
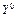 ={<
={<  ,
,  ,
,  > },
> },  Î
Î  (
( ),
),  =
=  ,
,
где  (
( ) – расширенное терм-множество лингвистической переменной ”КАЧЕСТВО1”;
) – расширенное терм-множество лингвистической переменной ”КАЧЕСТВО1”;  - нечеткое множество, описываемое функцией принадлежности вида
- нечеткое множество, описываемое функцией принадлежности вида  :
:  ®[0, 1];
®[0, 1];  - универсум:
- универсум:  = {0, 1, …, 10}. Значения лингвистической переменной ”КАЧЕСТВО1” даны в таблице 10.4.
= {0, 1, …, 10}. Значения лингвистической переменной ”КАЧЕСТВО1” даны в таблице 10.4.
Таблица 10.4. Значения параметра " КАЧЕСТВО1"
| Значение переменной ”КАЧЕСТВО1”
|  Î Î 
|
| Предельно низкое
|
|
| Почти низкое
|
|
| Низкое
|
|
| Чуть лучше, чем низкое
|
|
| Почти среднее
|
|
| Среднее
|
|
| Чуть лучше, чем среднее
|
|
| Почти высокое
|
|
| Высокое
|
|
| Чуть лучше, чем высокое
|
|
| Наивысшее
|
|
Нечеткое множество  определяется по известной формуле интегрирования
определяется по известной формуле интегрирования
 =
=  (
( )/
)/  . (10.4)
. (10.4)
Для получения текущего значения качества изделия используем одно из правил нечеткого условного вывода, получаемого аналитическими методами преобразований нечетких множеств:
 (
( (
( )
)  (
( ))=([
))=([ 
 ]´
]´ 

 ´
´  )Ç (Ø [
)Ç (Ø [ 
 ]´
]´ 

 ´ Ø
´ Ø  ).
).
На языке функций  ,
,  имеем:
имеем:  (
( (
( )
)  (
( )) =
)) =  (
( )
) 

 (
( ))Ù [(1-
))Ù [(1-  (
( ))
))  (1-
(1-  (
( ))] ] /(
))] ] /( ,
,  ). Последнее дает в качестве функции принадлежности отношения
). Последнее дает в качестве функции принадлежности отношения  (
( (
( )
)  (
( )) выражение
)) выражение

 1-
1-  (
( ), если
), если  (
( )<
)<  (
( ),
),
 (
( ,
,  ) = 1, если
) = 1, если  (
( )=
)=  (
( ), (10.5)
), (10.5)
 (
( ), если
), если  (
( )>
)>  (
( ).
).
Если с точки зрения технологии параметры  ,
,  неравнозначны, например при определении качества изделий большее значение имеет кривизна, чем температура, то в последнем выражении вместо
неравнозначны, например при определении качества изделий большее значение имеет кривизна, чем температура, то в последнем выражении вместо  и функций принадлежности
и функций принадлежности  (
( ),
),  (
( ), соответствующих результирующей функции (по виду
), соответствующих результирующей функции (по виду 
 )
)  (
( )=
)=  (
( )Ù
)Ù  (
( ), следуя принципу “выделения” и используя операцию “растяжения” (
), следуя принципу “выделения” и используя операцию “растяжения” ( ) нечетких множеств, необходимо представить входное нечеткое множество как
) нечетких множеств, необходимо представить входное нечеткое множество как  =
=  Ç
Ç  (
( ) и, соответственно,
) и, соответственно,  (
( )=
)=  (
( )Ù [
)Ù [  (
( )]0.5, где [
)]0.5, где [  (
( )]0.5 означает “более или менее
)]0.5 означает “более или менее  ”. Пример: для
”. Пример: для  =
=  = = несущественное получаем
= = несущественное получаем  (
( )=1/0+0.95/1+0.89/2+0.84/3+0.77/4+ +0.7/5+0.63/6+0.55/7+0.45/8+0.32/9+0/10 и
)=1/0+0.95/1+0.89/2+0.84/3+0.77/4+ +0.7/5+0.63/6+0.55/7+0.45/8+0.32/9+0/10 и  = 1/0+0.9/1+0.8/2+0.7/3+0.6/4+ +0.5/5+0.4/6+0.3/7+0.2/8+0.1/9+0/10.
= 1/0+0.9/1+0.8/2+0.7/3+0.6/4+ +0.5/5+0.4/6+0.3/7+0.2/8+0.1/9+0/10.
Для уяснения связи  ,
,  с
с  используем экспертное правило: “Если
используем экспертное правило: “Если  несущественное и
несущественное и  более или менее несущественное, то
более или менее несущественное, то  наивысшее иначе
наивысшее иначе  предельно низкое.” Из табл. 10.4 значению переменной наивысшее соответствует
предельно низкое.” Из табл. 10.4 значению переменной наивысшее соответствует  =10. Используем формулы для
=10. Используем формулы для  ,
,  (
( ), аналогичные для
), аналогичные для  ,
,  (
( ) – (10.1), (10.3) при
) – (10.1), (10.3) при  =1:
=1:
 =
=  [(
[( (
( )-1)
)-1)  ], (10.6)
], (10.6)
 (
( )=1-
)=1-  ê
ê  -
-  [(
[( (
( )-1)
)-1)  ]ê, (10.7)
]ê, (10.7)
где (10.6) при известной величине

дает

, определяющее лингвистическую переменную “КАЧЕСТВО1”, а (10.7) по всем табличным значениям

- функции принадлежности элементов нечеткого множества

, соответствующего найденному значению лингвистической переменной.
Зная  =10, из (10.6) находим
=10, из (10.6) находим  =
=  , а из (10.7) по аналогии с
, а из (10.7) по аналогии с  имеем
имеем  = наивысшее = 0/0+0.1/1+0.2/2+0.3/3+0.4/4+0.5/5+0.6/6+0.7/7+ +0.8/8+0.9/9+1/10. Полученные частные значения
= наивысшее = 0/0+0.1/1+0.2/2+0.3/3+0.4/4+0.5/5+0.6/6+0.7/7+ +0.8/8+0.9/9+1/10. Полученные частные значения  ,
,  позволяют строить матрицу нечетких бинарных отношений
позволяют строить матрицу нечетких бинарных отношений  (
( (
( )
)  (
( )) по (10.5), где
)) по (10.5), где  =
=  ,
,  (
( )=
)=  (
( ) – табл. 10.5.
) – табл. 10.5.
Таблица 10.5. Матрици отношений  (
( (
( )
)  (
( ))
))
 

|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 0.1
| 0.2
| 0.3
| 0.4
| 0.5
| 0.6
| 0.7
| 0.8
| 0.9
|
|
|
|
| 0.1
| 0.2
| 0.3
| 0.4
| 0.5
| 0.6
| 0.7
| 0.8
|
|
|
|
|
| 0.1
| 0.2
| 0.3
| 0.4
| 0.5
| 0.6
| 0.7
|
| 0.1
|
|
|
|
| 0.1
| 0.2
| 0.3
| 0.4
| 0.5
| 0.6
|
| 0.2
| 0.1
|
|
|
|
| 0.1
| 0.2
| 0.3
| 0.4
| 0.5
|
| 0.3
| 0.2
| 0.1
|
|
|
|
| 0.1
| 0.2
| 0.3
| 0.4
|
| 0.4
| 0.3
| 0.2
| 0.1
|
|
|
|
| 0.1
| 0.2
| 0.3
|
| 0.5
| 0.4
| 0.3
| 0.2
| 0.1
|
|
|
|
| 0.1
| 0.2
|
| 0.6
| 0.5
| 0.4
| 0.3
| 0.2
| 0.1
|
|
|
|
| 0.1
|
| 0.7
| 0.6
| 0.5
| 0.4
| 0.3
| 0.2
| 0.1
|
|
|
|
|
| 0.8
| 0.7
| 0.6
| 0.5
| 0.4
| 0.3
| 0.2
| 0.1
|
|
|
|
| 0.9
| 0.8
| 0.7
| 0.6
| 0.5
| 0.4
| 0.3
| 0.2
| 0.1
|
|
Пример расчета:
00.  =
=  =0,
=0,  =
=  =0; из ранее определенных нечетких множеств
=0; из ранее определенных нечетких множеств  и
и  находим по их первым элементам
находим по их первым элементам  (
( )=1,
)=1,  (
( )=0. Тогда из (10.5) получаем
)=0. Тогда из (10.5) получаем  (
( ,
,  )=
)=  (
( )=0;
)=0;
10.  =
=  =1,
=1,  =
=  =0; для второго элемента из
=0; для второго элемента из  имеем
имеем  (
( ) =
) =
= 0.9, для первого элемента из  сохраняется
сохраняется  (
( ) =0;
) =0;  (
( ,
,  ) = =
) = =  (
( ) =0;
) =0;
…………………………………………………………………………………..
100.  =
= 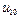 =10,
=10,  =
=  =0;
=0;  (
(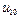 )=0,
)=0,  (
( )=0;
)=0;  (
( ,
,  )=1;
)=1;
01.  =
=  =0,
=0,  =
=  =1;
=1;  (
( )=1,
)=1,  (
( )=0.1;
)=0.1;
 (
( ,
,  )=
)=  (
( )=0.1;
)=0.1;
……………………………………………………………………………………
91.  =
=  =9,
=9,  =
=  =1;
=1;  (
( ) =0.1,
) =0.1,  (
( ) = 0.1;
) = 0.1;  (
( ,
,  ) = =
) = =  (
( ) =1;
) =1;
101.  =
= 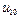 =10,
=10,  =
=  =1;
=1;  (
(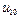 )=0,
)=0,  (
( )=0.1;
)=0.1;  (
(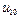 ,
,  ) =1-
) =1-
-  (
( ) = 0.9 и т.д.
) = 0.9 и т.д.
При любых текущих  =
=  ,
,  =
=  по формулам (10.3), (10.2) находим текущие нечеткие множества
по формулам (10.3), (10.2) находим текущие нечеткие множества  ,
,  . Для нахождения
. Для нахождения  =
=  воспользуемся формулой “композиционного вывода”
воспользуемся формулой “композиционного вывода”
 =
=  (
( (
( ))=
))=  (
( (
( ))o
))o  (
( (
( ),
),  (
( ))=
))=
=  o
o  (
( (
( )
)  (
( ))=
))=  (
( (
( )Ù
)Ù  (
( ,
,  ))/
))/  . (10.8)
. (10.8)
В качестве входного параметра для определения угла поворота манипулятора-сортировщика вводим нечеткое множество  , формирующее лингвистическую переменную ”КАЧЕСТВО2” в виде тройки
, формирующее лингвистическую переменную ”КАЧЕСТВО2” в виде тройки
 ={<
={<  ,
,  ,
,  > },
> },  Î
Î  (
( ),
),  =
=  .
.
Значения переменной ”КАЧЕСТВО2” показаны в табл. 10.6. Для
Таблица 10.6. Значения переменной " КАЧЕСТВО2"
| Значение переменной ”КАЧЕСТВО2”
|  Î Î 
|
| Неустранимый дефект
|
|
| Возможна повторная обработка
|
|
| На следующую операцию
|
|
отображения  ®
®  зададим следующее. Пусть
зададим следующее. Пусть  =
=  È
È  È
È  . При этом
. При этом  Ç
Ç  Ç
Ç  =Æ, например,
=Æ, например,  ={0, 1, …, 4},
={0, 1, …, 4},  = {5, 6, 7},
= {5, 6, 7},  ={8, 9, 10}.
={8, 9, 10}.
Отметим, что $  Î
Î  ½
½  (
( )=
)= 
 (
( ) – “сильнейший” (с наибольшим значением
) – “сильнейший” (с наибольшим значением  (
( )). Осуществим переход, связывающий множества
)). Осуществим переход, связывающий множества  ,
,  ,
,  с тремя положениями манипулятора-сортировщика:
с тремя положениями манипулятора-сортировщика:
 0, если
0, если  Î
Î  ,
,
 = 1, если
= 1, если  Î
Î  , (10.9)
, (10.9)
2, если  Î
Î  .
.
Нечеткое множество
 =
=  (
( )/
)/  , (10.10)
, (10.10)
где
 (
( )=1-
)=1-  ô
ô  -
-  ô,
ô,  =
=  . (10.11)
. (10.11)
Угол поворота манипулятора-сортировщика выражается в виде нечеткого множества  , которое формирует лингвистическую переменную “УГОЛ” в виде тройки
, которое формирует лингвистическую переменную “УГОЛ” в виде тройки
 ={<
={<  ,
,  ,
,  > },
> },  Î
Î  (
( ),
),  =
=  .
.
Значения переменной “УГОЛ” приведены в табл.10.7. Переменная 
Таблица 10.7. Значения переменной " УГОЛ"
| Значения переменной “УГОЛ”
|  Î Î 
|
| Малый
|
|
| Средний
|
|
| Большой
|
|
находится обычным путем:
 =
=  (
( )/
)/  . (10.12)
. (10.12)
Зададим углы поворота манипулятора  Î [900, 2700], т. е.
Î [900, 2700], т. е.  =900,
=900, 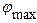 =2700. В соотношении (10.12) функция принадлежности
=2700. В соотношении (10.12) функция принадлежности  (
( ) рассчитывается по формуле
) рассчитывается по формуле
 (
( )=1-
)=1-  ê
ê  -
-  [(
[( (
( )-
)-
-1)  ] ê,
] ê,  =
=  . (10.13)
. (10.13)
По аналогии с (10.5) для построения нечеткого бинарного отношения, характеризующего логическую связь между качеством изделия и углом  , воспользуемся экспертным заключением:
, воспользуемся экспертным заключением:
“Если  неустранимый дефект, то
неустранимый дефект, то  малый, иначе
малый, иначе  большой ”.
большой ”.
Как и ранее, используя соответствующие формулы (10.10)-(10.13), табл.10.6 для  = 0 и табл. 10.7 для
= 0 и табл. 10.7 для  = 0, находим:
= 0, находим:  = неустранимый дефект =1/0+0.5/1+0/2,
= неустранимый дефект =1/0+0.5/1+0/2,  =малый = 1/0+0.5/1+0/2.
=малый = 1/0+0.5/1+0/2.
Для получения нечеткого множества, соответствующего текущему углу поворота манипулятора как логического следствия, в качестве нечеткого бинарного отношения воспользуемся выражением
 (
( (
( )
)  (
( ))=(
))=( ´
´ 

 ´
´  )Ç (Ø
)Ç (Ø  ´
´ 

 ´ Ø
´ Ø  ),
),
где 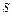 обозначает
обозначает 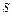 -логику. Или
-логику. Или  (
( (
( )
)  (
( )) =
)) =  (
( )
) 

 (
( ))Ù ((1-(
))Ù ((1-( ))
))  (1-
(1-  (
( )) ] /(
)) ] /( ,
,  ). По аналогии с (10.5)
). По аналогии с (10.5)
 1, если
1, если  (
( )=
)=  (
( ),
),
 (
( ,
,  ) = (10.14) 0, если
) = (10.14) 0, если  (
( )¹
)¹  (
( ).
).
Согласно этой формуле и (10.10), (10.12) строим матрицу отношений  (
( (
( )
)  (
( )) - табл. 10.8. На основе табл. 10.8 рассчитываем
)) - табл. 10.8. На основе табл. 10.8 рассчитываем
Таблица 10.8. Матрица отношений  (
( (
( )
)  (
( ))
))
нечеткое множество 

Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
|

Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...
|
ОПРЕДЕЛЕНИЕ ЦЕНТРА ТЯЖЕСТИ ПЛОСКОЙ ФИГУРЫ Сила, с которой тело притягивается к Земле, называется силой тяжести...
СПИД: морально-этические проблемы Среди тысяч заболеваний совершенно особое, даже исключительное, место занимает ВИЧ-инфекция...
Понятие массовых мероприятий, их виды Под массовыми мероприятиями следует понимать совокупность действий или явлений социальной жизни с участием большого количества граждан...
|
ФАКТОРЫ, ВЛИЯЮЩИЕ НА ИЗНОС ДЕТАЛЕЙ, И МЕТОДЫ СНИЖЕНИИ СКОРОСТИ ИЗНАШИВАНИЯ Кроме названных причин разрушений и износов, знание которых можно использовать в системе технического обслуживания и ремонта машин для повышения их долговечности, немаловажное значение имеют знания о причинах разрушения деталей в результате старения...
Различие эмпиризма и рационализма Родоначальником эмпиризма стал английский философ Ф. Бэкон. Основной тезис эмпиризма гласит: в разуме нет ничего такого...
Индекс гингивита (PMA) (Schour, Massler, 1948) Для оценки тяжести гингивита (а в последующем и регистрации динамики процесса) используют папиллярно-маргинально-альвеолярный индекс (РМА)...
|
 - значение
- значение  из таблицы 10.3. Пример:
из таблицы 10.3. Пример:  =1;
=1;  ,
,  такие, что для каждого по (10.1)
такие, что для каждого по (10.1)  =0 (
=0 ( =0 в табл.10.3 соответствует значение переменной ПАРАМЕТР =несущественное). Тогда из (10.3), табл.10.3, (10.3) и (10.2) имеем:
=0 в табл.10.3 соответствует значение переменной ПАРАМЕТР =несущественное). Тогда из (10.3), табл.10.3, (10.3) и (10.2) имеем:  =
=  = несущественное = 1/0+0.9/1+0.8/2+0.7/3+
= несущественное = 1/0+0.9/1+0.8/2+0.7/3+
 дает
дает  , определяющее лингвистическую переменную “КАЧЕСТВО1”, а (10.7) по всем табличным значениям
, определяющее лингвистическую переменную “КАЧЕСТВО1”, а (10.7) по всем табличным значениям  - функции принадлежности элементов нечеткого множества
- функции принадлежности элементов нечеткого множества  , соответствующего найденному значению лингвистической переменной.
, соответствующего найденному значению лингвистической переменной.

 Î [
Î [  ,
, 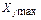 ],
],  =
=  , где [
, где [  ={<
={<  ,
,  ,
,  > },
> },  (
( ),
),  =
=  , где
, где  , принимающей значения в интервале [0, 1] для всех
, принимающей значения в интервале [0, 1] для всех  [(
[( (
( ], (10.1)
], (10.1) (
( (
( )/
)/  ê
ê  , формирующего лингвистическую переменную ”КАЧЕСТВО1”, описываемого тройками вида
, формирующего лингвистическую переменную ”КАЧЕСТВО1”, описываемого тройками вида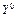 ={<
={<  ,
,  (
( ),
),  =
=  :
:  (
( (
( (
( )
)  (
( ))=([
))=([ 

 имеем:
имеем:  (
(
 1-
1-  (
( (
( (
( (
( ) нечетких множеств, необходимо представить входное нечеткое множество как
) нечетких множеств, необходимо представить входное нечеткое множество как  =
=  ], (10.6)
], (10.6) ê
ê  , а из (10.7) по аналогии с
, а из (10.7) по аналогии с  ,
, 
 =0,
=0,  =0; из ранее определенных нечетких множеств
=0; из ранее определенных нечетких множеств  )=0. Тогда из (10.5) получаем
)=0. Тогда из (10.5) получаем  (
( =1,
=1, 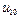 =10,
=10,  =1;
=1;  =9,
=9,  ,
,  по формулам (10.3), (10.2) находим текущие нечеткие множества
по формулам (10.3), (10.2) находим текущие нечеткие множества  ,
,  . Для нахождения
. Для нахождения  воспользуемся формулой “композиционного вывода”
воспользуемся формулой “композиционного вывода” =
=  (
( o
o  (
( , формирующее лингвистическую переменную ”КАЧЕСТВО2” в виде тройки
, формирующее лингвистическую переменную ”КАЧЕСТВО2” в виде тройки ={<
={<  ,
,  ,
,  ),
),  .
. Î
Î  È
È  È
È  . При этом
. При этом  Î
Î 
 0, если
0, если  = 1, если
= 1, если  (
( (
( ô
ô  , которое формирует лингвистическую переменную “УГОЛ” в виде тройки
, которое формирует лингвистическую переменную “УГОЛ” в виде тройки ={<
={<  ,
,  ,
,  ),
),  Î
Î  (
( Î [900, 2700], т. е.
Î [900, 2700], т. е.  =900,
=900, 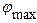 =2700. В соотношении (10.12) функция принадлежности
=2700. В соотношении (10.12) функция принадлежности  (
( ) рассчитывается по формуле
) рассчитывается по формуле ê
ê  ] ê,
] ê,  (
( )
)  ))=(
))=(
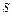 обозначает
обозначает  (
( ))
))  1, если
1, если  (
( (
(




