Построение и расчет агрегатных индексовПринципы и методы исчисления индексов рассмотрим на следующем примере. Пример 1 Имеются следующие данные о количестве выработанной продукции и ценах.
Индивидуальные индексы цен вычислим по формуле:
где p1 – цена единицы изделия в отчетном периоде, p0 – цена единицы изделия в базисном периоде.
Чтобы определить, как изменились цены в среднем по всем изделиям, определим общий индекс цен (Jp). Для исчисления общего индекса цен следует, прежде всего, перейти от совокупности элементов, непосредственно не поддающихся суммированию, которыми являются цены на отдельные виды изделий, к другой совокупности, сумма элементов которой дает экономически осмысленную величину. Этот переход осуществляется с помощью соизмерителей (весов). Для исчисления общего индекса цен в качестве весов может выступать количество изделий (q). Произведение цен на количество изделий ( Чтобы выявить изменение только цены, следует при расчете индекса цен исключить влияние на его величину изменения количества произведенной продукции. Для этого мы должны в качестве весов взять объем продукции какого-то одного периода. Какого? Базисного или отчетного? При решении вопроса о выборе весов следует руководствоваться исключительно экономическими соображениями, т.е. задачей, которая стоит перед конкретным индексом. Изменение цен, как правило, интересно знать на продукцию отчетного периода, поэтому в качестве весов следует взять продукцию отчетного периода. Тогда
В нашем примере общий индекс цен будет равен:
Это значит, что цены по всем изделиям в отчетном периоде по сравнению с базисным снизились в среднем на 7, 4%. Такой расчет позволяет определить не только изменение цен в процентах, но и абсолютный прирост (уменьшение) стоимости всей продукции за счет изменения цен. Она исчисляется как разница между числителем и знаменателем общего индекса цен.
В нашем примере Это значит, что за счет снижения цен в отчетном периоде по сравнению с базисным в среднем на 7, 4%, стоимость произведенной продукции уменьшилась на 27 тыс.д.е.. Если бы в качестве весов мы взяли продукцию базисного периода (q0), то задачи, поставленные перед данным индексом мы не смогли бы решить, а индекс цен имел бы иной смысл. Для всех индексов качественного показателя (цен, себестоимости, заработной платы, урожайности, производительности труда и т.п.) следует помнить следующее правило: расчет абсолютных сумм прироста (уменьшения) в отчетном периоде по сравнению с базисным за счет изменения качественного показателя следует производить на основе индексов, исчисленных на продукцию отчетного периода. Индивидуальные индексы физического объема продукции исчислим по формуле В нашем примере:
При исчислении общего индекса количественного показателя, каким является физический объем продукции, в качестве весов берется качественный показатель. В нашем примере весами выступают цены. При этом следует иметь в виду, что в индексах количественного показателя веса берутся на уровне базисного периода.
Объем произведенной продукции по всем изделиям увеличился в отчетном периоде по сравнению с базисным на 14, 4%. Разница между числителем и знаменателем
За счет изменения физического объема производства стоимость продукции увеличилась на 46 тыс.д.е. По данным нашего примера можно определить и индекс стоимости продукции. В индексе стоимости продукции в качестве индексируемой величины выступает стоимость продукции, равная произведению цены на количество продукции
В нашем примере:
Стоимость продукции отчетного периода больше стоимости продукции базисного периода на 5, 9%. Абсолютное выражение изменения стоимости продукции можно определить как разницу между числителем и знаменателем индекса стоимости продукции:
Данная система индексов позволяет разложить изменение общей величины по факторам. Поскольку стоимость продукции есть результат действия двух факторов (цены и объема производства), то изменение каждого из них влечет за собой изменение и стоимости продукции. Изменение стоимости за счет изменения цены определим как разницу между числителем и знаменателем индекса цен:
а за счет изменения объема продукции – как разницу между числителем и знаменателем индекса физического объема продукции:
При этом В нашем примере абсолютный прирост стоимости продукции составит
Стоимость продукции в отчетном периоде увеличилась по сравнению с базисным на 19 тыс.д.е. Это изменение обусловлено двумя факторами: изменением цен и изменением физического объема продукции.
Как отмечалось выше, величина стоимости продукции обусловлена воздействием двух факторов – цен и физического объема продукции. Индекс стоимости продукции так же связан с индексами цен и физического объема продукции. Причем между индексами существует та же взаимосвязь, что и между явлениями. Поскольку стоимость продукции равна произведению цен на объем произведенной продукции, то и В нашем примере:
Используя данное соотношение между взаимосвязанными индексами, можно определить любой из трех индексов, если 2 из них известны, т.е.
При исчислении индексов за ряд периодов можно рассчитывать цепные и базисные индексы. Причем, если для всех индексов берутся веса на уровне какого-то одного периода, то такой индексный ряд называется индексным рядом с постоянными весами. Если веса берутся на уровне разных периодов, - то с переменными весами. Правило для индексного ряда с постоянными весами – произведение цепных индексов равно соответствующему базисному индексу.
|
,
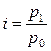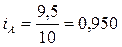или 95, 0% - цена по изделию А снизилась в отчетном периоде по сравнению с базисным на 5%.
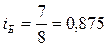или 87, 5% - цена по изделию Б снизилась в отчетном периоде по сравнению с базисным на 12, 5%.
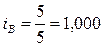или 100% - цена по изделию В в отчетном периоде не изменилась.
) есть стоимость произведенной продукции по каждому изделию. Сумма стоимости по каждому изделию даст общую стоимость всей произведенной продукции.
.
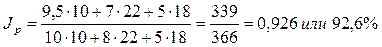
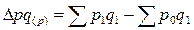, где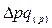
- абсолютный прирост (уменьшение) стоимости продукции в отчетном периоде по сравнению с базисным за счет изменения цен;
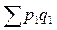- фактическая стоимость продукции отчетного периода;
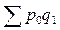- стоимость продукции отчетного периода при базисных ценах.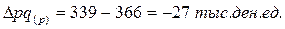
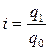
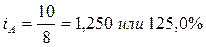- объем произведенной продукции по изделию А увеличился в отчетном периоде по сравнению с базисным на 25%.
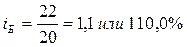- объем произведенной продукции по изделию Б увеличился в отчетном периоде по сравнению с базисным на 10%.
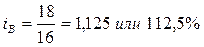- объем произведенной продукции по изделию В увеличился в отчетном периоде по сравнению с базисным на 12, 5%.
.
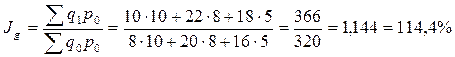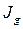покажет абсолютный прирост (уменьшение) стоимости продукции по всем изделиям в отчетном периоде за счет изменения физического объема.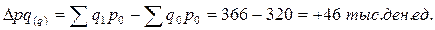
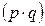.Следовательно: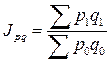
.
,
.
.
.
.
.
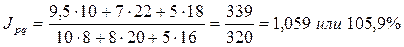
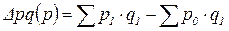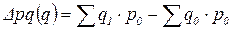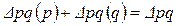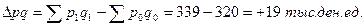
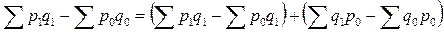
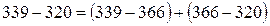
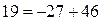
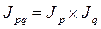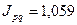
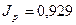
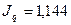
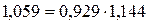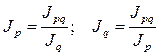