Пример 2. Из 2500 рабочих трёх цехов завода подвергнуто пропорциональному типическому отбору 200 человек, которые по проценту выполнения норм выработки распределились
Из 2500 рабочих трёх цехов завода подвергнуто пропорциональному типическому отбору 200 человек, которые по проценту выполнения норм выработки распределились следующим образом:
Принимая, что в каждой группе произведена случайная повторная выборка, определить: 1. Возможные пределы среднего процента выполнения норм выработки всеми рабочими завода (с вероятностью 0, 954). 2. Возможные пределы доли рабочих, выполняющих нормы выработки не менее чем на 100% (с вероятностью 0, 997). 3. Необходимую численность выборки при определении среднего процента выполнения норм выработки, чтобы с вероятностью 0, 954, предельная ошибка выборки не превышала 1%. 4. Необходимую численность выборки при определении доли рабочих, выполняющих нормы выработки не менее чем на 100%, чтобы предельная ошибка выборки не превышала 3% (с вероятностью 0, 954). Решение: 1) Средняя ошибка выборочной средней при типической выборке (повторный отбор) исчисляется по формуле:
где
Для нахождения выборочной средней и средней внутригрупповой дисперсии составим расчётную таблицу: Таблица 5 Расчетная таблица
Определяем выборочную среднюю:
Дисперсии типических групп (внутригрупповые дисперсии) определим по формуле:
Средняя ошибка выборки будет равна:
Предельная ошибка выборки составит:
Следовательно, с вероятностью 0, 954 можно утверждать, что средний процент выполнения норм выработки всеми рабочими завода находится в пределах 2) Выборочная доля
Средняя ошибка выборочной доли при типическом повторном отборе определяется по формуле:
Средняя ошибка доли будет равна:
Тогда предельная ошибка: Следовательно, с вероятностью 0, 997, можно утверждать, что доля рабочих завода, выполняющих нормы выработки не менее, чем на 100%, находится в пределах 3) Объём выборки, обеспечивающий предельную ошибку выборки не более чем 1%, будет равен (с вероятностью 0, 954)
4) Объём выборки при исчислении доли, обеспечивающий предельную ошибку выборки не более чем на 3% (с вероятностью 0, 954)
Пример 3 Из 30 бригад (по 10 человек каждая) отобрано 3 бригады, рабочие которых распределились по возрасту следующим образом:
Определить: 1) с вероятностью 0, 683 средний возраст рабочих всех 30 бригад; 2) объём выборки, обеспечивающий с вероятностью 0, 997 предельную ошибку выборки, не превышающую 1 года.
Средний возраст рабочих по каждой бригаде определим по формуле средней арифметической простой, как сумму возрастов всех рабочих бригады, делённую на число рабочих. Так, средний возраст рабочих первой серии (бр. №5) будет равен
Аналогичным образом определяем средний возраст рабочих следующих серий: второй = третьей = Средний возраст рабочих выборочной совокупности составит Для серийной выборки
где
Поскольку численность всех бригад одинаковая, можно использовать не взвешенную среднюю
Тогда
С вероятностью 0, 683 мы можем утверждать, что средний возраст всех рабочих будет не меньше 34, 69 года и не больше 35, 71 года. 2) Объём выборки, обеспечивающий с вероятностью 0, 997 предельную ошибку выборки, не превышающую 1 года должен быть не менее 7 бригад .
|


 - средняя внутригрупповая дисперсия, равная средней взвешенной из дисперсий отдельных типических групп.
- средняя внутригрупповая дисперсия, равная средней взвешенной из дисперсий отдельных типических групп.

 (
(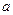 =
=105)
=
=105)
 (
( =10)
=10)

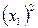


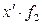











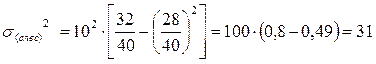



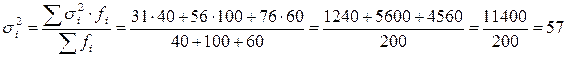

 .
. , т.е. от 106, 94% до 109, 06%.
, т.е. от 106, 94% до 109, 06%.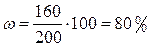
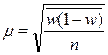
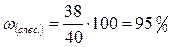 ;
; 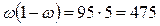
 ;
; 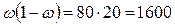
 ;
; 

 .
.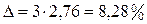 .
. , т. е. от 71, 72% до 88, 28%.
, т. е. от 71, 72% до 88, 28%.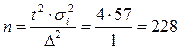 рабочих.
рабочих. рабочих.
рабочих.
 года
года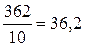 года,
года,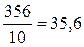 года.
года. года.
года. ,
, - межгрупповая дисперсия, определяемая по формуле
- межгрупповая дисперсия, определяемая по формуле .
.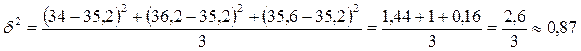

 года
года .
. бригад.
бригад.


