Средний арифметический и средний гармонический индексы
Приведенные выше формулы расчета индексов называются агрегатными. Расчет индексов по агрегатным формулам возможен, если есть полные данные о физическом объеме продукции и о ценах как на уровне отчетного так и базисного периодов. В реальной действительности полные данные имеются не всегда. В таких случаях приходится исчислять индексы как среднюю взвешенную величину из индивидуальных индексов. Вопрос о выборе формы средней и системы весов при расчете индекса как среднего из индивидуальных решается на основе общего правила: агрегатный индекс – основная форма всякого индекса. Следствие этого правила – средний из индивидуальных индексов будет тогда правильным, когда он тождественен агрегатному индексу. Это означает, что средние из индивидуальных индексов не самостоятельные индексы, а преобразованная форма агрегатного индекса. При исчислении средних индексов могут быть использованы только две формы средних: средняя арифметическая и средняя гармоническая. Пример 2 Имеются следующие данные о продаже товаров:
Требуется определить общий индекс физического объема товарооборота. Агрегатная формула индекса физического объема товарооборота:
В нашем примере есть сведении о Из данной формулы выразим
где
В данном случае используем средний арифметический индекс.
Таким образом, количество проданных товаров увеличилось в отчетном периоде по сравнению с базисным на 7, 5%. Пример 3. Имеются следующие данные о реализации товаров:
Вычислить индивидуальные и общий индексы цен. Индивидуальные индексы:
Агрегатная формула общего индекса цен:
Объем товарооборота Из формулы индивидуального индекса цен Тогда
Это формула среднего гармонического индекса.
4. Индексный анализ динамики средних уровней качественных показателей. Средние уровни многих экономических явлений исчисляются на основе групповых средних. Например средняя себестоимость изделия А по двум предприятиям определяется исходя из средней себестоимости изделия А на каждом предприятии взвешенной по количеству изделий, произведенных на данном предприятии, т.е.
Индекс динамики средней себестоимости изделия А имеет следующую формулу:
На величину этого индекса оказывают влияние два фактора – изменение себестоимости на каждом предприятии и изменение объема продукции (удельного веса, структуры) отдельных предприятий. Поскольку в данном индексе используются веса разных периодов, то этот индекс называют индексом переменного состава. Индекс переменного состава характеризует изменение средней величины качественного показателя по всей совокупности: Для выявления влияния на изменение средней себестоимости изменения самой себестоимости рассчитывают индекс постоянного состава. который характеризует изменение величины качественного показателя в среднем по отдельным объектам совокупности: Чтобы исключить влияние структурных сдвигов на изменение средней себестоимости, среднюю себестоимость в базисном периоде корректируют на структуру фактического выпуска продукции. В общем виде формула индекса себестоимости фиксированного состава записывается так:
Для выявления влияния на изменение средней величины изменения структуры продукции исчисляют индекс влияния структурных сдвигов.
При этом взаимосвязь между индексами выражается следующей формулой:
Расчет индексов постоянного, переменного состава и влияния структурных сдвигов покажем на следующем примере. Пример 4 Имеются следующие данные о деятельности трех строительных организаций:
Рассчитайте индексы заработной платы переменного и постоянного составов, а также индекс влияния структурных сдвигов. Объясните результаты расчетов.
Решение: 1. Индекс переменного состава характеризует изменение средней величины качественного показателя – заработной платы – по всей совокупности и рассчитывается по формуле:
Средняя заработная плата по всем строительным организациям в отчетном периоде по сравнению с базисным увеличилась на 5, 4%. На величину этого индекса оказали влияние два фактора: изменение самой заработной платы и изменение в структуре рабочих. 2. Индекс постоянного состава изучает изменение качественного показателя за счет динамики самого показателя, исключая влияние структурных сдвигов: как видно, в формуле данного индекса коэффициенты при весах q неизменны (фиксируются на уровне отчетного периода):
Рассчитаем индекс заработной платы постоянного состава:
Таким образом, средняя заработная плата по всем строительным организациям повысилась на 5, 2% за счет изменения самой заработной платы. 3. Индекс влияния структурных сдвигов характеризует изменение средней величины качественного показателя за счет изменения структуры совокупности и не учитывает влияние динамики самой качественной величины (размер заработной платы фиксируется на уровне базисного периода):
Рассчитаем, чему равен данный индекс в нашем случае:
Таким образом, изменение структуры среднегодовой численности строительно-монтажных рабочих повлекло увеличение средней заработной платы на 0, 2%. Между индексами переменного и постоянного состава и индексом влияния структурных сдвигов существует взаимосвязь: произведение индекса постоянного состава и индекса влияния структурных сдвигов дает индекс переменного состава.
С помощью взаимосвязи экономических индексов проверим правильность произведенных ранее расчетов:
Ответ: средняя заработная плата по трем строительным организациям в отчетном периоде по сравнению с базисным увеличилась на 5, 4%. Данное увеличение на 5, 2% было вызвано динамикой самой заработной платы по всем строительным организациям и на 0, 2% – изменением структры численности строительно-монтажных рабочих данных организаций. ТЕМА: СТАТИСТИЧЕСКИЙ АНАЛИЗ ВЗАИМОСВЯЗИ
|
.
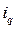
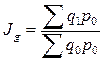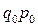. Кроме того, мы имеем индивидуальные индексы количества проданных товаров по каждой товарной группе. Как известно 
.
: 
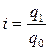и подставим это значение 
,
- индивидуальный индекс физического объема товарооборота;
- товарооборот базисного периода.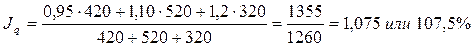
по каждой товарной группе имеем по условию задачи.
выражаем 
: 
и это значение 
.
.
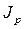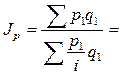
, т.е. в среднем цены снизились на 5, 4%.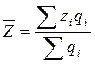
: 
.
.
.
.
.
.
.
.
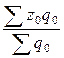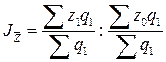
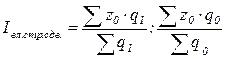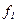
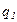
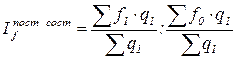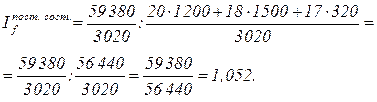
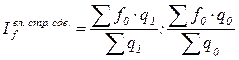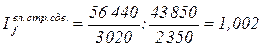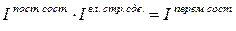