Распределение ресурсов
Задачи распределения ресурсов в отличие от задач учета потребностей ресурсов относятся к оптимизационному типу и могут рассматриваться как для односетевых, так и для многосетевых комплексов работ. По результатам решения задачи распределения ресурсов составляют календарный план выполнения комплекса работ, т. е. для каждой работы указываются даты ее начала и окончания с учетом обусловленной технологией последовательности их выполнения таким образом, чтобы удовлетворялось оптимальное значение целевой функции и не нарушались ограничения, которые определяются при постановке задачи распределения ресурсов. Известно чрезвычайно большое число разнообразных постановок данных задач, которые можно разбить на три основные группы в зависимости от принимаемого критерия оптимальности и вида ограничений: - задачи распределения ресурсов, при котором обеспечивается минимизация времени осуществления комплекса работ при выполнении заданных ограничений на используемые ресурсы; - задачи распределения ресурсов, при котором удовлетворяется наилучшее значение некоторого показателя качества использования ресурсов при заданных сроках выполнения всего комплекса, чаще всего в данной постановке производится минимизация максимальных значений потребляемых ресурсов; - задачи распределения ресурсов в смешанных постановках, где, например, для некоторых сетей в многосетевой разработке минимизируется время выполнения комплекса работ при заданных уровнях используемых ресурсов, а для других — минимизируются уровни потребления ресурсов при заданных сроках выполнения комплекса. Методы решения задач распределения ресурсов можно условно подразделить на: 1) методы математического программирования; 2) эвристические; 3) комбинированные. Методы первого направления реализуются средствами целочисленного линейного, нелинейного, динамического и статистического программирования. Ко второму направлению относятся методы, в основе которых лежат эвристические правила (метод последовательного фронтального распределения, метод последовательного растяжения, метод последовательной корректировки плана и т. п.). Комбинированные методы решения задач распределения ресурсов основываются на сочетании методов математического программирования и эвристических методов и могут быть условно разделены на четыре группы: 1) методы, использующие результат решения задачи эвристическими методами в качестве исходных данных для дальнейшего решения с помощью методов математического программирования; 2) методы, осуществляющие предварительное эвристическое разбиение основной задачи на частные задачи, решаемые методами математического программирования; 3) методы, использующие эвристические правила при формировании условий задачи, решаемой методами математического программирования; 4) усеченные методы математического программирования. Методы распределения ресурсов можно разделить на методы с переменной и постоянной интенсивностью потребления ресурсов, используемых на работах. Методы распределения ресурсов с переменной интенсивностью потребления ресурсов предполагают возможность изменения интенсивности потребления ресурса в течение выполнения любой работы, что приводит в конечном итоге к сокращению продолжительности выполнения работы и к увеличению коэффициента использования ресурса. В результате решения данных задач получается зависимость оптимального значения потребного ресурса от продолжительности каждой работы сетевой модели. Для небольших сетевых моделей задачу распределения ресурсов с переменной интенсивностью можно решить с помощью интуитивного перераспределения ресурсов. В случае использования графиков больших размерностей необходимо применение методов математического программирования. Методы распределения ресурсов с постоянной интенсивностью потребления ресурсов, используемых на работах, можно разделить на две большие группы: - методы с фиксированной интенсивностью потребления ресурсов; - методы с фиксированным диапазоном возможных значений интенсивностей потребления ресурсов. При использовании методов, относящихся к первой группе, заранее задается интенсивность потребления ресурсов и осуществляется поиск оптимальных сроков начала и окончания работ. Недостатком данных алгоритмов является то, что качество решения, определяемое в первую очередь коэффициентом использования ресурсов, во многом зависит от интенсивностей потребления ресурсов, которые назначаются на основании опыта и инструкции. При использовании методов второй группы осуществляется поиск оптимальных интенсивностей потребления ресурсов внутри заданных диапазонов, а также сроков начала и окончания работы. Размерности данных задач, решаемых классическими методами математического программирования для реальных сетевых моделей, являются неприемлемыми для современной вычислительной техники. В связи с трудностями постановки и решения задач распределения ресурсов эти вопросы выходят за рамки дисциплине «Календарное планирование в управлении качеством» и могут быть изучены по специальной литературе в области прикладной математики. Общая модель планирования проекта с распределением ресурсов Математические модели распределения ресурсов обеспечивают составление календарного плана на стадии исходного планирования. Они реализуются в двух основных постановках в зависимости от принимаемого критерия оптимальности и вида ограничений: - модель расчета календарного плана многосетевой модели, который обеспечивает минимизацию максимального отклонения сроков завершения каждого комплекса от директивного или минимизацию сроков завершения каждого комплекса при выполнении заданных ограничений на использование ресурсов и учитывает приоритеты комплексов (1-й тип задачи календарного планирования); - модель расчета календарного плана, который удовлетворяет минимизации максимального отклонения потребностей в ресурсах от уровня их наличия при выполнении заданных ограничений на сроки выполнения каждого из планируемых комплексов работ (2-й тип задачи календарного планирования). Каждая из моделей планирования применяется в зависимости от конкретных условий планирования. Следует отметить, что при решении практических задач, как правило, возникает необходимость применения так называемой смешанной постановки. При этом под смешанной постановкой понимается одновременное использование двух основных постановок. Для одной части комплексов решается задача расчета календарного плана, который обеспечивает минимизацию максимального отклонения сроков завершения каждого комплекса от директивного срока или минимизацию сроков завершения каждого комплекса при выполнении заданных ограничений на использование ресурсов и учете приоритетов комплексов. Для другой части комплекса решается задача расчета календарного плана, который обеспечивает минимизацию максимального отклонения потребностей в ресурсах от уровня их наличия при выполнении заданных ограничений на сроки выполнения каждого из планируемых комплексов. Первой стадией планирования является предварительное планирование. Целью предварительного планирования является исследование условий реализации комплекса работ проекта. На этой стадии определяется ряд узловых событии, представляющих собой результаты выполнения отдельных законченных частей проекта. Основной целью такого учета является выявление практических требований к потребным ресурсам. В том случае когда осуществляется предварительное планирование многотемных (многосетевых) комплексов работ, важным моментом является предварительная увязка результатов решения задачи объемного планирования, обеспечивающей формирование плана с установленными технико-экономическими показателями, с задачей календарного планирования, т. е. решение ряда вопросов, связанных с формированием тематического плана, обеспечивающего выполнение основных объемных показателей. Эта проблема является одной из важнейших на этапе предварительного планирования, Ее содержание поясним на модели формирования тематического плана, минимизирующего дисбаланс между структурой располагаемых и потребных ресурсов. Формирование тематического плана сводится к выбору такого набора технологически независимых комплексов работ, которые обеспечивают оптимальный вариант тематического плана, позволяющий улучшить использование располагаемых ресурсов. При многотемном планировании рассматриваемые комплексы работ могут различаться по степени важности, что приводит к необходимости учета различных уровней приоритетов тем. Введем обозначения: Е — целевая функция; М — планируемый уровень объема работ по всем комплексам на планируемый период; j — текущий индекс темы (комплекса работ); i — текущий индекс вида ресурсов; n — количество заявочных тем; т — количество планируемых ресурсов; Задача формирования тематического плана может быть решена в двух постановках. 1. Выбрать перечень комплексов работ, который бы обеспечил минимальное отклонение суммарных потребных объемных показателей работ по темам от запланированного уровня при условии, что потребные объемы ресурсов не превышают располагаемых объемов; данная задача формализуется как оптимизационная с альтернативными переменными:
2. Выбрать перечень комплексов работ, который бы обеспечил минимальное отклонение потребных объемов ресурсов от их располагаемых объемов при условии, что суммарные потребные объемные показатели работ по темам не меньше запланированного уровня. Данная задача формализуется в виде:
Решение данных задач обеспечивает формирование тематического плана, структура ресурсов которого будет соответствовать располагаемым ресурсам, что, в конечном счете, создает лучшие условия решения основной задачи предварительного планирования — оценки достижимости целей комплексов работ. Материалы предварительного планирования служат основой для утверждения директивных сроков выполнения комплексов работ, размеров ассигнований, привлечения к участию в работе исполнителей. После этого приступают к решению задачи исходного планирования. Исходное планирование комплекса работ является второй стадией планирования проекта. На стадии исходного планирования осуществляется расчет календарного плана комплекса работ. В процессе расчета исходного плана производится: построение сетевой модели комплекса работ; привязка сетевой модели к нормативной базе; расчет календарного плана выполнения комплекса работ. Процесс разработки сетевой модели основывается на изучении технологических процессов, которые в дальнейшем формализовано описывают в виде графа. Если сетевая модель отображает сравнительно небольшие и несложные программы, то построение сетевой модели осуществляется на основе правил построения сетевых графиков. При построении сетевых моделей для больших и сложных программ прибегают к помощи таблицы структурного анализа. В том случае, когда производится построение сетевых моделей, входящих в многосетевой комплекс, предварительно проводится анализ программ (процессов) с целью выявления типовых сетевых моделей, т. е. таких графиков, топология которых описывает последовательность работ для нескольких программ. Выделение типовых сетевых моделей обеспечивает значительное сокращение объема подготовительных работ, повышает качество исходных данных, практически исключает ошибки в построении сетевых моделей. Привязка сетевой модели к нормативной базе заключается в определении для каждой работы сетевой модели значений основных параметров из числа следующих: объем, продолжительность, интенсивность потребления ресурсов. Чаще всего в качестве параметров при описании работы используются продолжительность и интенсивность потребления ресурсов. При выборе значений параметров работ следует иметь в виду, что значение интенсивности потребления ресурсов находится в пределах от минимально до максимально допустимого значения интенсивности потребления ресурсов на работе. Пределы изменения значений интенсивности потребления ресурсов определяются физическим содержанием работы и используемых ресурсов. Так, если в качестве ресурсов фигурируют люди, то минимально допустимое значение интенсивности потребления ресурса не может быть меньше 1, так как планирование работы, на которой используется меньше одного исполнителя, недопустимо. С другой стороны, если в вычислительном центре имеется пять компьютеров, то максимально допустимое значение интенсивности потребления ресурсов не может быть более пяти, так как фронт работы для большего числа операторов не будет обеспечен. Особо следует подчеркнуть, что от выбора значений интенсивностей потребления ресурсов и продолжительностей работ зависит результат решения задачи расчета календарного плана. «Удачный» выбор значений этих параметров будет способствовать увеличению коэффициента использования ресурсов, а, следовательно, и повышению качества решения. К сожалению, в настоящее время эффективных методов решения данной задачи не существует, и исходными данными при расчете календарного плана являются значения интенсивностей потребления ресурсов и продолжительностей работ, поэтому выбор этих значений основывается на опыте или интуиции специалиста. При расчете календарного плана необходимо для каждой работы каждой сетевой модели (если планирование многосетевое) указать точную дату начала и окончания каждой работы с тем, чтобы в данных временных границах работа была обеспечена соответствующим ресурсом в необходимом количестве. Кроме этого, календарный план должен удовлетворять ряду требований организационного характера, таких как директивные сроки начала и окончания всего проекта и отдельных его этапов и работ, приоритет одних проектов перед другими и пр. Основная задача расчета календарного плана состоит в обеспечении баланса по ресурсам и времени. На рисунке 4.1 представлен план, не сбалансированный по времени и ресурсам, на рисунке 4.2 — план, не сбалансированный по ресурсам, на рисунке 4.3 — полностью сбалансированный план.
|

 — коэффициент веса важности j -й темы;
— коэффициент веса важности j -й темы;  — норма затрат ресурса вида i на тему вида j; Сj — объем работ по теме j; Ri — располагаемый объем i -го ресурса; xj = 0, 1 — булевы переменные, если xj = 1 — тема включается в тематический план, если xj = 0 — тема не включается в тематический план.
— норма затрат ресурса вида i на тему вида j; Сj — объем работ по теме j; Ri — располагаемый объем i -го ресурса; xj = 0, 1 — булевы переменные, если xj = 1 — тема включается в тематический план, если xj = 0 — тема не включается в тематический план.
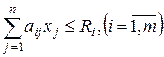
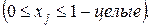 (4.1)
(4.1)