АППАРАТ ЛИНЕЙНОЙ ПЕРСПЕКТИВЫ
Вычислите стандартизованные показатели рождаемости у лиц соответствующих возрастных групп на территориях А и Б и сделайте соответствующие выводы. За стандарт принять полусумму составов населения по возрасту на территориях А и Б.
СПИСОК ЛИТЕРАТУРЫ: 1. Лисицын Ю.П. Общественное здоровье и здравоохранение. М.: ГЭОТАР-МЕД. 2002. – 508с. 2. Медик В.А., Токмачев М.С., Фишман Б.Б. Статистика в медицине и биологии: Руководство в 2-х томах /под ред. Ю.М. Комарова – М.: Медицина, 2000. – 412с. 3. Мерков А.М., Поляков Л.Е. Санитарная статистика. Л.: «Медицина», Ленинградское отделение, 1974. – 384с. 4. Общественное здоровье и здравоохранение. Под ред. проф. В.А. Миняева, проф. Н.И. Вишнякова. Учебник для студентов. М.: «МЕДпресс-информ»., 2002. – 518с. 5. Юрьев В.К., Куценко Г.И. Общественное здоровье и здравоохранение. С.-Пб.: «Петрополис»., 2000. – 585с.
М.А. Айгунян Методическое пособие По теме «Перспектива» Для студентов направления «Архитектура» Москва Российский университет дружбы народов ВВЕДЕНИЕ
Наглядность изображения – одна из главных задач архитектурного чертежа. Изображения фасадов с построенными на них тенями не всегда позволяют понять и представить себе композиционное решение. С этой целью строятся перспективные изображения зданий, комплекса зданий. Оценить решение интерьера также невозможно без построения его перспективы. Поэтому умение грамотно построить перспективное изображение один из необходимых навыков для архитекторов и дизайнеров. В зависимости от того, на какой поверхности строится перспективное изображение, перспектива подразделяется на следующие виды: – линейная перспектива – перспективное изображение, построенное на плоскости; – панорамная или цилиндрическая перспектива – перспективное изображение, построенное на внутренней поверхности цилиндра вращения; – купольная или сферическая перспектива – перспективное изображение, построенное на внутренней поверхности сферы. В настоящем разделе рассматривается только линейная перспектива.
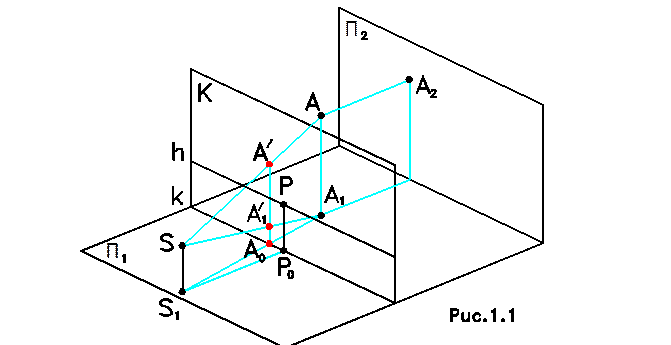
АППАРАТ ЛИНЕЙНОЙ ПЕРСПЕКТИВЫ Метод центрального проецирования является основным средством построения перспективных изображений. На рис.1.1 представлены плоскости проекций П1 и П2, а также дополнительная плоскость K, называемая картинной плоскостью или просто картиной, расположенная перпендикулярно горизонтальной плоскости проекций П1. В данном примере для упрощения построений картинная плоскость располагается параллельно фронтальной плоскости проекций, что не является обязательным. Линия пересечения картины с горизонтальной плоскостью проекций называется основанием картины. Точка A расположена в пространстве между плоскостями П2 и K. Это пространство называется предметным. Наблюдатель находится в пространстве перед плоскостью K. Это пространство называется промежуточным пространством. Пространство за наблюдателем называется мнимым пространством. Точка S1 на горизонтальной плоскости проекций, в которой стоит наблюдатель, называется точкой стояния. Точка S, находящаяся в промежуточном пространстве и на уровне которой расположены глаза наблюдателя, называется точкой зрения. Луч SP, проведенный из точки зрения перпендикулярно картинной плоскости, называется главным лучом. Точка его пересечения с картинной плоскостью P называется главной точкой картины. Линия h, проходящая через главную точку P параллельно основанию картины, называется линией горизонта. Точки A1 и A2 являются горизонтальной и фронтальной проекциями точки A на плоскости проекций П1 и П2. При пересечении с основанием картины луча, проведенного из точки S1 в точку A1, образуется точка A0. Пересечение луча, исходящего из точки S в точку A, с вертикальной линией из точки A0 образуется точка A/. Точка A/ называется перспективной проекцией точки A на плоскость K. (Точки S, S1, A0, A1, A, A/ лежат в одной вертикальной плоскости.) Однако, одна проекция A/ не дает обратимого чертежа точки A, т.к. для любой точки, принадлежащей лучу SA, перспективная проекция совпадает с точкой A/. Для того, чтобы чертеж обладал обратимостью, строится вторичная перспективная проекция точки A, полученная в пересечении луча SA1 с картинной плоскостью в точке A1/. Точка A1/ называется вторичной перспективной проекцией точки A. Комплекс точек A/ и A1/ однозначно определяет положение точки A.
Для построения перспективы отрезка AB (рис.1.2) необходимо для точки B провести построения как для точки A. Перспектива отрезка прямой для линейной перспективы также является отрезком прямой. Поэтому, соединив точки A/ и B/, а также точки A1/ и B1/ прямой линией, можно получить перспективную проекцию A/B/ и вторичную проекцию A1/B1/ отрезка AB.
На рис.1.3 изображен комплексный чертеж отрезка AB, а также картинная плоскость K, которая по отношению к комплексному чертежу является фронтальной плоскостью уровня. Фронтальная проекция плоскости K совпадает с фронтальной плоскостью проекций П2. На этом чертеже показано, как, имея комплексный чертеж, можно построить перспективное изображение. Однако на практике перспективное изображение строится другим более простым способом. Возвращаясь к изображению на рис.1.2, перспективную проекцию отрезка AB можно построить через полную перспективу прямой, на которой лежит отрезок AB. Для этого необходимо продолжить прямую по обе стороны от точек A и B. Прямая при ее продолжении за точку A пересечет картинную плоскость в точке N. Очевидно, что перспектива точки N, лежащей в картинной плоскости, совпадет с этой точкой N/≡ N, а ее вторичная перспективная проекция совпадет с основанием точки N/ (N1/≡ N0). На рис.1.4 для получения точек N/ и N1/ достаточно продолжить горизонтальную проекцию A1B1 до пересечения с горизонтальной проекцией картинной плоскости K, а на фронтальной проекции картинной плоскости продолжить фронтальную проекцию A2B2 до пересечения с соответствующей линией связи. Если продолжить отрезок за точку B, то точки прямой будут удаляться от картинной плоскости (рис.1.2). При этом луч, исходящий из точки S, в пределе займет положение, параллельное отрезку AB (соответственно проекции луча займут положение, параллельное соответствующим проекциям, на рис.1.2, 1.4 и далее одинаковыми штрихами обозначены параллельные прямые). В точке F/ будет находиться, так называемый, конец прямой, а отрезок N/F/ будет называться полной перспективой прямой, на которой лежит отрезок AB. В точке F1/ будет находиться конец вторичной перспективной проекции прямой. Отрезок N1/F1/ будет называться полной вторичной перспективной проекцией прямой, на которой лежит отрезок AB. Точка F/ называется точкой схода прямой, точка F1/ называется точкой схода вторичной перспективной проекции. Точка F0 называется основанием точки схода. Точка схода вторичной перспективной проекции F1/ находится на линии горизонта h. Аналогичные построения выполнены на рис.1.4 при совмещении картинной плоскости с комплексным чертежом.
Таким образом, для построения перспективы отрезка необходимо иметь комплексный чертеж, на котором строится начало прямой N и точка схода F/. Далее отдельно стоится картина (рис.1.5), на которой вдоль ее основания откладываются точки N1/≡ N0 и F0. Все горизонтальные расстояния берутся с горизонтальной проекции комплексного чертежа (обычно они откладываются на основании картины от основания главной точки P0). От точек N0 и F0 по вертикали откладываются расстояния, равные высотам точек N/ и F/, которые берутся с фронтальной проекции комплексного чертежа (т.к. точки N/ и F/ находятся в картинной плоскости, то их высоты будут на картине в натуральную величину). Соединяя точки N/ и F/, а также N1/ и F1/, можно получить полную перспективу прямой и ее вторичной проекции. Если на основании картины от точки P0 отложить расстояния до точек A0 и B0 (взятые с горизонтальной проекции комплексного чертежа) и провести через них вертикальные прямые, то они отсекут на полной перспективе и ее вторичной проекции соответствующие перспективную проекцию отрезка A/B/ и его вторичную перспективную проекцию A1/B1/. Очевидно, что точка схода для параллельных прямых будет находиться в одном месте, т.е. параллельные прямые имеют общую точку схода (рис.1.6).
|