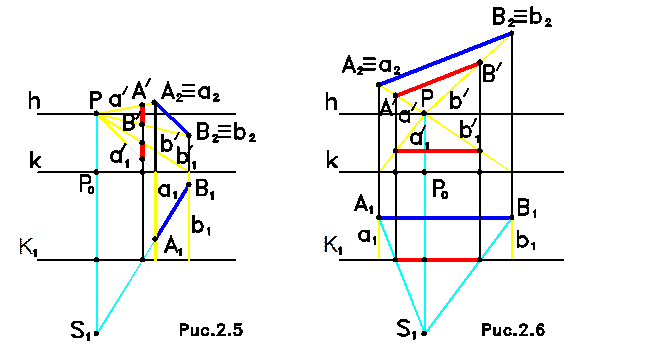ПЕРСПЕКТИВА ПРЯМЫХ ЧАСТНОГО ПОЛОЖЕНИЯ

При построении перспективы реальных архитектурных форм чаще всего приходится строить перспективные проекции прямых частного положения или имеющих какие-либо особые свойства. Поэтому учет особенностей при построении перспективы таких прямых дает дополнительные возможности для упрощения построений.

1. Перспектива горизонтальных прямых (рис.2.1). Точка схода горизонтальных прямых находится на линии горизонта. Действительно, прямая, исходящая из точки зрения и параллельная горизонтальной прямой, также будет горизонтальной, и поэтому точка схода F^/ будет находиться на линии горизонта, т.е. точки F₁^/ и F^/ совпадут.

2. Перспектива прямых, перпендикулярных картинной плоскости (рис.2.2). Точка схода прямых, перпендикулярных картине, совпадает с главной точкой картины, т.к. луч, исходящий из точки зрения и параллельный таким прямым, пересекает картинную плоскость в точке P. На рис.2.2 построена перспектива двух отрезков AB и CD.

3. Перспектива горизонтальных прямых, расположенных под углом 45⁰ к картинной плоскости (рис.2.3). Точками схода горизонтальных прямых, расположенных под углом 45⁰ к картинной плоскости, являются дистанционные точки. Дистанционными точками называются точки D¹ и D², расположенные на линии горизонта на расстоянии от главной точки P, равном расстоянию от точки зрения до картинной плоскости SP (т.е. PD¹ = PD² = SP). Прямые, исходящие из точки S и параллельные прямым AB и BC, также расположены под углом 45⁰ к картине и пересекают ее в точках D¹ и D².

4. Перспектива прямых, расположенных под углом 45⁰ к картинной плоскости (рис.2.4). Окружность с центром в точке P и радиусом PD¹ = PD² является геометрическим местом точек схода всех прямых, расположенных под углом 45⁰ к картине. Такие прямые могут быть построены как образующие конуса вращения с углом при вершине 45⁰ и осью, расположенной перпендикулярно картине. На рис.2.4 построена точка схода произвольной прямой, расположенной под углом 45⁰ к картине.

5. Перспектива прямых, горизонтальная проекция которых проходит через точку стояния (рис.2.5). Перспективная проекция прямых, горизонтальная проекция которых проходит через точку стояния, является вертикальной прямой. На рис.2.5 для построения перспективы отрезка построена полная перспектива двух прямых a и b, перпендикулярных картине и имеющих точку схода P. Вертикальная прямая, проходящая через точки A₀ = B₀, пересечется с полной перспективой прямых a и b в точках A^/ и B^/, а с их вторичной проекцией в точках A₁^/ и B₁^/. Соединение точек A^/ и B^/, а также точек A₁^/ и B₁^/ позволит получить перспективу отрезка AB.

6. Перспектива прямых, параллельных картинной плоскости (рис.2.6).Перспективная проекция прямой, параллельной картинной плоскости, параллельна самой прямой. Т.к. такая прямая не имеет ни начала, ни точки схода, то ее перспективная проекция также, как в предыдущем случае строится через перспективу прямых a и b, перпендикулярных картинной плоскости и проходящих через точки A и B. Вертикальные прямые из точек A₀ и B₀ пересекутся с перспективной проекцией a^/ и b^/, а также с вторичной перспективной проекцией a₁^/ и b₁^/ в точках A^/, B^/ и A₁^/, B₁^/ соответственно.

Плоские фигуры, параллельные картине, в перспективе являются подобными фигурами.