Деление отрезка
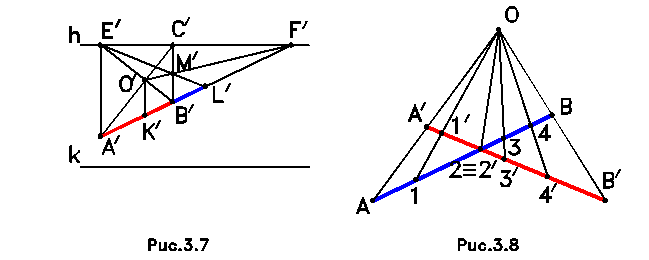
1. Деление горизонтального отрезка пополам (рис.3.7). Для того, чтобы разделить горизонтальный отрезок AB в перспективе пополам, необходимо достроить прямоугольник ABCE, у которого сторона CE лежит на линии горизонта, а стороны AE и BC вертикальные. Вертикальная прямая, проведенная через точку пересечения диагоналей O, разделит отрезок AB на две равные части. Прямая, проведенная через точки E и M до пересечения с продолжением отрезка AB в точке L, позволит построить отрезок BL, равный заданному отрезку AB.
2. Деление отрезка на пропорциональные части (рис.3.8). Отрезок A/B/ разделен на пропорциональные части в перспективе в том же отношении, что и отрезок AB, если существуют три пары точек A и A/, 2 и 2 /, B и B/, через которые можно провести прямые, пересекающиеся в одной точке O.
На основании этого утверждения можно разделить горизонтальный отрезок A/B/ на пропорциональные части (рис.3.9). Для этого через ближайший конец отрезка A/ проводится горизонтальный отрезок, разделенный в заданном отношении, последняя его точка (5) соединяется с конечной точкой B/ прямой, которая доводится до линии горизонта. Прямые, проведенные из точки схода O в точки деления отрезка, являются горизонтальными и параллельными (в перспективе) и разделят отрезок A/B/ в том же отношении, что и отрезок 1-5. Т.е. для горизонтального отрезка AB достаточно двух пар точек (A/ и 1, B/ и 5), т.к. заведомо предполагалось расположить точку O на линии горизонта. В случае, если прямая занимает общее положение, необходимо разделить в пропорциональном отношении ее вторичную проекцию, а вертикальные прямые, проведенные из точек деления, разделят сам отрезок в том же отношении (рис.3.10).
|