Примеры задач для самостоятельного решения. 1.Дана функция спроса на некоторый товар: QD = 8 - 0,5Р1.Дана функция спроса на некоторый товар: QD = 8 - 0, 5Р. При какой цене коэффициент прямой эластичности спроса равен –0, 5? Решение: воспользуемся формулой коэффициента эластичности спроса по цене: QD = 8- 0, 5Р, в результате получим, что Далее: -0, 5 = Ответ: цена равна 5, 3.
2.Какая цена даст наибольшую выручку, если функция спроса такова: QD = 900 - 3Р? Решение: используем формулу линейной функции спроса: Ответ: максимальная цена равна 150.
3.Эластичность спроса на медицинские услуги по цене равна 0, 2. Эластичность спроса по доходу составляет 3. За год стоимость медицинских услуг возросла на 15%, а доход увеличился на 15%. Как изменится спрос на медицинские услуги? Решение: общее изменение спроса составит: 0, 2 * 15% + 3 * 10% = 33%. Ответ: спрос изменится на 33%.
4.Определите, на сколько процентов должна измениться цена на товар, чтобы это привело к увеличению его предложения с 4 млн. до 6 млн. штук, если Es = 0, 7? Решение: воспользуемся формулой коэффициента эластичности предложения: Es = DQ/DP * P1/Q1; 0, 7 = (6 – 4)/DP * Р1/4. DP представим как: Р2–Р1, а Р2 распишем как исходное значение плюс его прирост или: (Р1+DP1)–Р1. Отсюда: 2/DP * Р1/4=0, 7; 1/2DP =0, 7; 2DP =1/0, 7; DP = 1/(2*0, 7); DP = 0, 7, или 70%. Ответ: цена должна измениться на 70%.
5.В результате повышения цены с 5 долл. до 6 долл. величина спроса на товар сократилась с 9 млн. штук до 7 млн. штук в год. Определите коэффициент дуговой эластичности спроса по цене. Решение: Ответ: ЕD = - 1, 4.
|
, где 
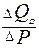представим как производную функции
равно: -0, 5.
; 4 = 0, 75Р; Р = 5, 3.
. Максимальная цена имеет место в точке, где ЕD = 1. В этой точке Р = а/2b. Отсюда, Р = 900/(2*3) = 150.
