Критерии оценки работы систем массового обслуживания
Существует множество критериев оценки систем массового обслуживания. В этом разделе рассмотрены те четыре показателя, которые обычно используются в качестве критериев при математическом исследовании систем массового обслуживания. Однако не следует делать вывод, что эти показатели являются наиболее важными на практике. На самом деле для некоторых реальных систем они не могут быть четко определены, то есть они не существуют.
Пусть: Di ‑ задержка в очереди требования i; Wi = Di + Si ‑ время ожидания в системе требования i; Q (t) - число требований в очереди в момент времени t, L (t) ‑ число требований в системе в момент времени t (Q (t) плюс число требований, которые находятся на обслуживании в момент времени t). Тогда показатели
и
(если они существуют) называются установившейся средней задержкой и установившимся средним временем ожидания. Соответственно показатели
и
(если они существуют) называются установившимся средним по времени числом требований в очереди и установившимся средним по времени числом требований в системе. Здесь и выражение «с вероятностью 1» дано для соблюдения математической правильности и не имеет особого практического значения. Допустим, что К наиболее общим и нужным результатам для оценки систем массового обслуживания относятся уравнения сохранения Q = ld и L = lw (4.5) выполняющиеся для любой системы массового обслуживания, где существуют показатели d и w. Еще одно важное уравнение связывает время ожидания требования в системе с установившейся задержкой требования в очереди и средним временем обслуживания: W = d + E (S) (4.6) Следует обратить внимание, что упомянутые выше критерии оценки работы системы могут быть аналитически вычислены для систем массового обслуживания M / M / s (s ≥ 1), M / G /1 при любом распределении G и для некоторых других систем. В общем же случае, чтобы аналитическое решение стало возможным, распределение времени между поступлениями требований, распределение времени обслуживания или обеих этих величин должно быть экспоненциальным или разновидностью экспоненциального распределения Эрланга k -ro порядка. Например, можно аналитически показать, что установившееся среднее число требований в системе М/М/1 вычисляется по формуле L = r/ (r ‑ 1) (4.7) которое отображено на графике рис. 4.2 как функция r. Заметим, что L — явно нелинейная функция r, и для r > 0, 8 график L экспоненциально возрастает. Хотя формула, определяющая L, выведена специально для систем массового обслуживания М / М /1, нелинейное поведение, показанное на рис. 4.3, свойственно системам массового обслуживания вообще.
Рис. 4.3. График L = r/ (r ‑ 1) для системы массового обслуживания M / M /1 Еще один интересный и наглядный пример аналитического решения ‑ вычисление установившейся средней задержки в очереди для системы массового обслуживания M / G /1 по формуле
где Var(S) обозначает дисперсию распределения времени обслуживания. Таким образом, если E (S) имеет большее значение, тогда перегрузка (в данном случае измеряемая как d) будет большей, чего и следовало ожидать. По формуле можно обнаружить и менее очевидный факт: перегрузка также увеличивается, когда изменчивость распределения времени обслуживания возрастает, даже если среднее время обслуживания остается прежним. Интуитивно это можно объяснить так: дисперсия случайной величины времени обслуживания может принять большое значение (поскольку она должна быть положительной), то есть единственное устройство обслуживания будет занято длительное время, что приведет к увеличению очереди. 4.3.6. Компоненты дискретно-событийной имитационной Хотя моделирование применяется к самым разнообразным реальным системам, все дискретно-событийные имитационные модели включают ряд общих компонентов. Логическая организация этих компонентов позволяет обеспечивать программирование, отладку и последующее изменение программы имитационной модели. В частности, дискретно-событийная имитационная модель, которая использует механизм продвижения времени от события к событию и написана на универсальном языке программирования (С, FORTRAN и пр.), содержит следующие компоненты: § состояние системы — совокупность переменных состояния, необходимых для описания системы в определенный момент времени; § часы модельного времени — переменная, указывающая текущее значение модельного времени; § список событий — список, содержащий время возникновения каждого последующего типа событий; § статистические счетчики - переменные, предназначенные для хранения статистической информации о характеристике системы; § программа инициализации — подпрограмма, устанавливающая в исходное состояние имитационную модель в момент времени, равный 0; § синхронизирующая программа - подпрограмма, которая отыскивает следующее событие в списке событий и затем переводит часы модельного времени на время возникновения этого события; § программа обработки событий — подпрограмма, обновляющая состояние системы, когда происходит событие определенного типа (для каждого типа событий существует отдельная программа обработки событий); § библиотечные программы — набор подпрограмм, применяемых для генерации случайных наблюдений из распределений вероятностей, которые были определены как часть имитационной модели; § генератор отчетов — подпрограмма, которая считывает оценки (со статистических счетчиков) критериев оценки работы и выдает отчет по окончании моделирования; § основная программа — подпрограмма, которая вызывает синхронизирующую программу, для того чтобы определить следующее событие, а затем передает управление соответствующей событийной программе с целью обеспечения заданного обновления состояния системы. Основная программа может также контролировать необходимость прекращения моделирования и вызывать генератор отчетов по его окончании.
Рис. 4.4. Блок-схема системы ДСИМ с механизмом продвижения от события к событию Блок-схема программной системы дискретно-событийного имитационного моделирования показана на рис. 4.4. Моделирование начинается в момент времени, равный 0. При этом основная программа вызывает программу инициализации, которая устанавливает часы модельного времени в 0, затем задает исходное состояние системы, устанавливает в исходное состояние статистические счетчики и инициализирует список событий. После возвратая управления основной программе она вызывает синхронизирующую программу, чтобы определить тип ближайшего события. Если следующим должно произойти событие типа i, часы имитационного времени переводятся на время возникновения события типа i, и управление возвращается основной программе. Основная программа активизирует программу обработки событий i, при этом происходят три типа действий: первое ‑ обновляется состояние системы в соответствии с произошедшим событием типа i; второе ‑ собирается информация о критериях оценки работы системы путем обновления статистических счетчиков; третье - генерируется время возникновения будущих событий, и информация о нем добавляется в список событий. Часто при определении времени будущих событий возникает необходимость генерации случайных наблюдений с некоторым распределением вероятностей, поскольку такое наблюдение является реализацией (выборкой, как говорят статистики) некоторой случайной величины. После полного завершения обработки в программе обработки событий i или в основной программе выполняется проверка с целью определить (относительно некоторого условия останова), следует ли прервать моделирование. И если моделирование должно быть завершено, из основной программы вызывается генератор отчета, для того чтобы считать оценки (со статических счетчиков) необходимых критериев работы и создать отчет. Если время прекращения моделирования еще не настало, управление снова передается основной программе, и цикл «основная программа ‑ синхронизирующая программа ‑ основная программа ‑ программа обработки событий ‑ проверка условия прекращения имитации» повторяется до тех пор, пока условие останова не будет выполнено. Организация и функционирование дискретно-событийной моделирующей программы, в которой применяется механизм продвижения времени от события к событию, довольно типичны, если эта программа написана на универсальном языке (например, FORTRAN или С). Такой подход к имитационному моделированию называется планированием событий, поскольку время будущих событий явно указано в модели и запланировано в модельном будущем.
|

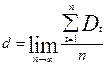 с вероятностью 1 (4.1)
с вероятностью 1 (4.1)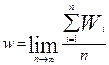 с вероятностью 1 (4.2)
с вероятностью 1 (4.2)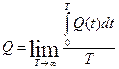 с вероятностью 1 (4.3)
с вероятностью 1 (4.3) с вероятностью 1 (4.4)
с вероятностью 1 (4.4) при n®∞ (с вероятностью 1) для некоторой системы массового обслуживания. Если выполняется очень большое (бесконечное) число экспериментов, эти средние задержки
при n®∞ (с вероятностью 1) для некоторой системы массового обслуживания. Если выполняется очень большое (бесконечное) число экспериментов, эти средние задержки  фактически в каждом эксперименте стремятся к конечной величине d. Заметьте, что r < 1 ‑ обязательное условие существования d, w, Q и L в системе массового обслуживания GI/G / s.
фактически в каждом эксперименте стремятся к конечной величине d. Заметьте, что r < 1 ‑ обязательное условие существования d, w, Q и L в системе массового обслуживания GI/G / s.
 (4.8)
(4.8)



