ПРЕОБРАЗОВАНИЯ ИЗМЕРИТЕЛЬНЫХ СИГНАЛОВ В СИ
Основным принципом получения и передачи измерительной информации является измерительные преобразования. Измерительные преобразования осуществляются различными физическими звеньями электрической цепи, которые называются измерительными преобразователями. В этом смысле СИ являются последовательностью (каскадом) измерительных преобразователей. В самом простом случае для реализации измерений необходимо осуществить две операции: воспроизведение и сравнение. Однако в реальной жизни обойтись этими двумя операциями не удаётся. Их намного больше. Вот некоторые из них: 1) первичные восприятия измеряемой величины и формирование измерительного сигнала; 2) функциональные (операторные) преобразования; 3) квантование; 4) дискретизация; 5) восстановление; 6. модуляция (демодуляция); 7) фильтрация; 8) запоминание; 9) регистрация. Связь между входными и выходными сигналами X(t) и Y(t) может быть в общем случае описана уравнением преобразования (связи)
где F – некоторая функция преобразования. Функции преобразования и преобразователи разделяются на два больших класса: · линейные; · нелинейные. Линейная функция преобразования удовлетворяет двум условиям суперпозиции: аддитивности и однородности:
где a1, a2=const. В результате взаимодействия с чувствительным элементом измеряемая величина преобразуется в промежуточный сигнал, который подвержен дополнительным преобразованиям (промежуточным преобразованим): усиление, выделение сигнала на мостовой схеме, суммирование и т.д. Функциональные преобразования реализуют: · изменением физической природы сигнала; · изменением размеров информативных параметров сигналов; · изменением неинформативных параметров сигналов; · масштабированием, т.е. созданием выходного сигнала, однорого с входным (при этом выходной сигнал имеет информативный параметр кратный по размерам информативному параметру информативному параметру входного сигнала). Нелинейные функциональные преобразования сигнала описываются нелинейной зависимостью выходного сигнала преобразователя от входного. Примеры нелинейных преоразований: 1) 2) 3) Кроме того, имеют место операторные преобразования типа: 1) 2) 3) Нелинейные преобразования сигнала используются в связи с необходимостью линеаризации общей характеристики СИ, автоматизации косвенных измерений, сжатия данных по оси значений и т.п. Преобразование сигналов реализуется звеньями измерительной цепи неизбежно сопровождается изменением выходных сигналов по отношению к входным во времени. Эти изменения объясняются внутренними динамическими процессами преобразования энергии. Поэтому в общем случае процесс преобразования сигналов описывается интегрально-дифференциальными уравнениями (ИДУ). Линейные системы описываются линейными дифференциальными уравнениями с постоянными коэффициентами.
Или в операторной форме:
где Уравнение (6.2) можно представить в виде
где (р) и В (р) – операторные многочлены. Для нахождения уравнения связи (функции преобразования) в виде
необходимо решить уравнение (6.1). Однако часто решение уравнения (6.1) затруднено, поэтому на практике прибегают к косвенному методу, а именно: любой сигнал x(t) представляют в виде аппроксимации, например ступенчатой, рис. 6.1.
Рис. 6.1. Ступенчатая аппроксимация сигнала x(t)
Если интервал Δ t уменьшается, то
В этом случае каждый из прямоугольников может быть представлен дельта функцией и можно использовать интеграл Дюамеля-Карсона. При этом переходной процесс можно записать с помощью импульсной переходной функцией
С использованием передаточной функции связь между Y(t) и X(t) может быть записана в виде
где Y(p) и X(p)- изображения по Лапласу Y(t) и X(t); К(р)- передаточная функция системы, причём она связанна с импульсной переходной функцией выражением
Для определения Y (t) в частотной области используются преобразования Фурье:
где Частная передаточная функция связанна с импульсной переходной функцией выражением
Аналого-цифровые преобразования (АЦП) сигнала позволяют аналоговый сигнал представить в виде числа. Принцип АЦП сводится к следующему. Пусть x0, x1, x2, …, xN, …, xP – упорядоченный равноинтервальный ряд величин возрастающих значений, в котором
Положим, что значение ∆ xk известно в единицах измеряемой величины x. Тогда значение любой величины из указанного ряда, например xN, равно порядковому номеру N, умноженному на ∆ xk, xN =N∆ xk. Если в результате сравнения неизвестной величины x и известных величин из указанного ряда оказалось, что xN < x < xN+1, то можно принять x В общем случае бесконечное множество размеров величины x в диапазоне от 0 до xP отражается ограниченным множеством P числовых значений, т.е. при АЦП происходит замена непрерывной измеряемой величины x, квантованной по уровню величиной xN. При этом величина ∆ xk называется шагом квантования. При АЦП практически всегда имеет место погрешность (погрешность квантования) так как бесконечное множество размеров x отражается ограниченным множеством значений P. Число N выражают либо в виде комбинаций цифр отсчета, либо в виде комбинаций условных сигналов. Комбинацию цифр в виде числа N называю кодом. Представление числа N в виде кода – кодированием. В широком смысле слова понятие«кодирование» означает операцию перевода по определённым правилам кодовых символов одного алфавита, отображающего формальный объект, в кодовые символы другого алфавита. В технике получило распространение цифровое кодирование. В общем случае числовое кодирование в измерении – это операция отображения количества единиц данной величины числом в данной системе счисления. Система счисления (СС) – это совокупность символов в виде цифровых знаков и правил, которые применяются для однозначного представления чисел и выражений количественной информации в числовой форме. Числовой код – это представление числа (результата измерений) в форме удобной для числовой обработки дискретными устройствами, передачи результатов измерений по каналам связи и т.п. СС разделяются на два класса: позиционные и непозиционные СС. Непозиционная система – это система, в которой значение знака не зависит от его положения по отношению к другим знакам. Позиционная система – это системам, в которой любое число N может быть представлена формулой
где В – основание СС; n – номер разряда числа; ai – знаки (цифры) системы. В зависимости от СС коды делятся на две группы: 1) числоимпульсные коды, в которых используется единичная СС; 2) цифровые коды, базирующееся на двоичной, десятичной и двоично-десятичной СС.
|

 - логарифмическое преобразование.
- логарифмическое преобразование. - степенное преобразование.
- степенное преобразование. , k, n=const – прочие не линейные преобразования.
, k, n=const – прочие не линейные преобразования. ,
, ,
,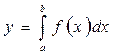 .
. .
.
 ,
,
 дифференциальный оператор по времени.
дифференциальный оператор по времени. ,
,


 .
.



 ,
,
 изображение Фурье соответственно y(t) и x(t).
изображение Фурье соответственно y(t) и x(t).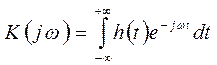 .
.
 xN = N∆ xk. Таким образом, имеется возможность характеризовать размер величины x именованным числом xN, которое принимается за значение величины x.
xN = N∆ xk. Таким образом, имеется возможность характеризовать размер величины x именованным числом xN, которое принимается за значение величины x. ,
,



