Принцип двойственности
Теорема: Пусть функция h (x 1,..., xn) реализована формулой h (x 1,..., xn) = = g (G 1,..., Gm) = g (f 1(x 1,..., xn),..., fm (x 1,..., xn)), где какие-то переменные могут быть фиктивными. Тогда h *(x 1,..., xn) = g *(f 1*(x 1,..., xn),..., fm *(x 1, …, xn)), это означает, что если функция задана некоторой формулой, то чтобы получить двойственную функцию, надо в этой формуле все знаки функций заменить на двойственные, 0 на 1, 1 на 0. Доказательство. h *(x 1,..., xn) = Если функция h (x 1,..., xn) реализуется формулой N [ f 1,..., fn ], то формулу, полученную из N заменой fi, входящих в нее, на fi * и реализующую функцию h *(x 1,..., xn), будем называть двойственной и обозначать N *(x 1,..., xn). Пример 4. Построить формулу, реализующую f *, если f = ((x Найдем (x Å y)* и (x
Из таблиц видно, что (x (x По принципу двойственности: f * = Тогда f = (f *)* = [ z (x Å y)]* = z Ú (x ~ y). Пример 5. Найти формулу для f* и показать, что она эквивалентна формуле N = (x Ú (z Å t)) f * = ((x Ú y Ú z)Å t ( = ( = =
|

 (
( 1,...,
1,...,  (f 1(
(f 1( (
( 1(
1( (
( ),..., ((
),..., (( ) = g *(f 1*(x 1,..., xn),..., fm *(x 1,..., xn)), что и требовалось доказать.
) = g *(f 1*(x 1,..., xn),..., fm *(x 1,..., xn)), что и требовалось доказать. y) Ú z) (y
y) Ú z) (y 
 y)* = x ~ y =
y)* = x ~ y =  = x
= x  y
y  ,
, y x
y x 
 y.
y.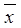 yz
yz 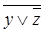 (x
(x  yz
yz  z (x
z (x  y Ú (
y Ú (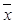 y Ú
y Ú 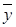 (x Å z Å 1)) = z (
(x Å z Å 1)) = z ( y Ú
y Ú  )) = z
)) = z 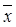 y Ú (z
y Ú (z  x Å z
x Å z  ) = z (
) = z (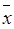 y Ú x
y Ú x  ) = z (x Å y).
) = z (x Å y). , если f = (xyz ~(t Ú x
, если f = (xyz ~(t Ú x 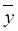 ))Ú
))Ú 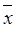 Ú y))(
Ú y))( t (
t ( Ú y)Ú (x Ú y Ú z)
Ú y)Ú (x Ú y Ú z)  )(
)( Ú t) =
Ú t) =

 t Ú (x Ú y Ú z)(
t Ú (x Ú y Ú z)( Ú x
Ú x 
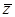 t Ú
t Ú  (x Ú (z Å t)).
(x Ú (z Å t)).


