Полные системы1. P 2 – полная система. 2. Система M ={ x 1& x 2, x 1Ú x 2, Пример 1. Неполные системы: {
Лемма (достаточное условие полноты)
Пусть система Доказательство. Пусть h(x1,..., xn) Î P2, т.к. U полна в Р2, то h(x1,..., xn) = =N[f1,..., fs,...] = N[L1[g1,..., gk],..., Ls[g1,..., gk],...] = U[g1,..., gk]. Здесь мы воспользовались тем, что для любого i 3. Система { x 1Ú x 2, Возьмем в качестве полной в Р 2 системы U ={ x 1Ú x 2, С помощью этой леммы докажем полноту еще ряда систем. 4. Система { x 1& x 2, 5. Система { x 1| x 2} полна в Р 2. Для доказательства возьмем в качестве полной в Р 2 системы U = { x 1& x 2,
6. Система { x 1 7. Система { x 1& x 2, x 1Å x 2, 0, 1}, U = { x 1& x 2, Следствие. Полином Жегалкина. f (x 1,..., xn) Î P 2, представим ее в виде формулы через конъюнкцию и сумму по модулю два, используя числа 0 и 1. Это можно сделать, так как { x 1& x 2, x 1Å x 2, 0, 1} полна в Р 2. В силу свойства x & (y Å z) = xy Å xz можно раскрыть все скобки, привести подобные члены, и получится полином от n переменных, состоящий из членов вида х Общий вид полинома Жегалкина:
где
|
} – полная система, т.к. любая функция алгебры логики может быть записана в виде формулы через эти функции.
}, {0, 1}.
U = { f 1, f 2,..., fs,...} полна в Р 2. Пусть B = { g 1, g 2,..., gk,...} – некоторая система из Р 2, причем любая функция fi Î U может быть выражена формулой над B, тогда система B полна в Р 2.
n fi может быть выражена формулой над B, поэтому fi=Li[gi,..., gk].
.
через х 1| x 2 :
= (x 1| x 2)|(x 1| x 2).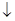
x 2} полна в Р 2. U = { x 1Ú x 2, 
}, 
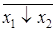= (x 1 
х 
... х 
, соединенных знаком Å. Такой полином называется полиномом Жегалкина.
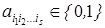, s = 0, 1,..., n, причем при s = 0 получаем свободный член а 0.
