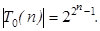Т0 - класс функций, сохраняющих константу 0Т 0 = { f (x 1,..., xn | f (0,..., 0) = 0, n = 1, 2,...}. Покажем, что Т 0 является собственным подмножеством Р 2, т.е. Т 0 ¹ Æ и Т 0 Ì Р (не совпадает с Р 2). Для этого достаточно привести примеры функций, входящих в Т 0, и примеры функций из Р2, не входящих в Т 0: x 1& x 2, x 1Ú x 2, x Î Т 0 и x 1| x 2, x 1 Число функций, зависящих от n переменных и принадлежащих Т 0, будет равно 2) T 1 – класс функций, сохраняющих константу 1. T 1 = { f (x 1,...) | f (1, 1,...) = 1}; x 1& x 2, x 1Ú x 2, x Î T 1, х 1Å х 2, x 1 Покажем, что [ T 1] Í T 1, обратное включение следует из определения формулы и замыкания. Так как тождественная функция входит в Т 1, можно рассмотреть Ф = f (f 1,..., fn) Î [ T 1], где f, f 1,..., fn Î T 1. Найдем Ф (1,..., 1) = f (f 1(1,..., 1),..., fn (1,..., 1)) = f (1,..., 1) = 1, следовательно, Ф = f (f 1,..., fn) Î T 1, отсюда следует [ T 1] = T 1.
|
x 2, 
Ï Т 0. Покажем далее, что [ Т 0] = Т 0. Вложение Т 0 Í [ Т 0] очевидно, так как по определению формулы любая функция из Т 0 является формулой над Т 0 и, следовательно, принадлежит [ Т 0]. Покажем, что [ Т 0]Í Т 0. Для этого надо показать, что Ф = f (f 1,..., fm) Î [ Т 0], если все функции f, f 1, f 2, f 3,..., f m Î Т 0. Надо заметить, что в формуле в качестве функции f 1 могут быть взяты переменные, которые мы договорились считать тождественными функциями. Тождественная функция принадлежит классу Т 0, поэтому достаточно показать, что Ф = f (f 1,..., fm) Î Т 0. Для этого рассмотрим следующую функцию: Ф (0,..., 0) = f (f 1(0,..., 0), f 2(0,..., 0),...) = f (0,..., 0) = 0.
