|
| Т 0
| Т 1
| L
| M
| S
|
|
| +
| -
| +
| +
| -
|
|
| -
| +
| +
| +
| -
|
| x 1 x 2
| +
| +
| -
| +
| -
|
| x 1Å x 2
| +
| -
| +
| -
| -
|
Согласно критериальной таблице, полной является и система {1, x 1 x 2, x 1Å x 2}. Константа 0 введена в эту систему для удобства, тогда мы можем записать полином Жегалкина в виде, где а  равны 0, если члены х
равны 0, если члены х  х
х  ... х
... х  , в полиноме отсутствуют.
, в полиноме отсутствуют.
4. Выясним, полна ли система  . Составим критериальную таблицу, очевидно
. Составим критериальную таблицу, очевидно  . Чтобы показать, что
. Чтобы показать, что  , достаточно найти одну функцию
, достаточно найти одну функцию  и
и  . Возьмем
. Возьмем  , удовлетворяющую требуемым условиям. Если f
, удовлетворяющую требуемым условиям. Если f  S\T0, то f(0,..., 0) = 1, f(1,..., 1)=0, следовательно, f
S\T0, то f(0,..., 0) = 1, f(1,..., 1)=0, следовательно, f  M, f
M, f  T1. Рассмотрим функцию h = x1x2
T1. Рассмотрим функцию h = x1x2  x2x3
x2x3  x1x3=1, набор ее значений (11101000), h
x1x3=1, набор ее значений (11101000), h  S\T0, но h
S\T0, но h  L. Следовательно, критериальная таблица имеет вид:
L. Следовательно, критериальная таблица имеет вид:
|
| Т 0
| Т 1
| L
| M
| S
|
L 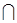 T 1 T 1
| -
| +
| +
| -
| -
|
| S \ T 0
| -
| -
| -
| +
| -
|
и А – полная система функций.
Определение. Система функций { f 1,..., fs,...} называется базисом в Р 2, если она полна в Р 2, но любая ее подсистема не будет полной. Например, система функций { x 1& x 2, 0, 1, x 1  x 2
x 2  x 3} – базис.
x 3} – базис.

 равны 0, если члены х
равны 0, если члены х  х
х  ... х
... х  , в полиноме отсутствуют.
, в полиноме отсутствуют. . Составим критериальную таблицу, очевидно
. Составим критериальную таблицу, очевидно  . Чтобы показать, что
. Чтобы показать, что  , достаточно найти одну функцию
, достаточно найти одну функцию  и
и  . Возьмем
. Возьмем  , удовлетворяющую требуемым условиям. Если f
, удовлетворяющую требуемым условиям. Если f  S\T0, то f(0,..., 0) = 1, f(1,..., 1)=0, следовательно, f
S\T0, то f(0,..., 0) = 1, f(1,..., 1)=0, следовательно, f  M, f
M, f  x2x3
x2x3 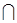 T 1
T 1



