В классе КНФ
Построение минимальных КНФ для частично определенной функции аналогично построению минимальных КНФ для всюду определенной функции. Алгоритм минимизации частично определенных функций в классе нормальных форм аналогичен алгоритму минимизации в классе нормальных форм для всюду определенных функций. Пример 1. В классе нормальных форм минимизировать частично определенную функцию f (x, y, z, t) = (1---010010-01--1) Решение. Минимизируем функцию f в классе ДНФ. 1. Строим сокращенную ДНФ для доопределения единицами f 1 функции f по таблице 3.9. Таблица 3.9
2. Строим матрицу покрытий коституент единицы в СДНФ для доопределения нулями f 0 функции f с помощью построенной сокращенной ДНФ для f 1 (таблица 3.10). Таблица 3.10
3. По таблице строим решеточный многочлен E = (2Ú 4)(5Ú 6)(3Ú 4)(1Ú 3)1 = 145 Ú 125 Ú 146 Ú 1236. 4. Строим все тупиковые ДНФ:
5. Из построенных тупиковых ДНФ выбираем минимальные:
Функции g 1 и g 3 есть минимальные доопределения функции f в классе ДНФ. Минимизируем теперь функцию f в классе КНФ. Для этого проведем минимизацию функции ` f в классе ДНФ Пусть h 0 и h 1 есть доопределение нулями и единицами соответственно функции ` f. Сокращенная ДНФ для
Матрица покрытия конституент единицы в СДНФ для h 0 с помощью простых импликант в сокращенной ДНФ для h 1 приведена в таблице 3.11. Таблица 3.11
3. Решеточное выражение E =5 (2 Ú 3 Ú 5) 2 (1Ú 4)(1Ú 6) = 25(1Ú 46) = 125 Ú 2446. 4. Строим две тупиковые ДНФ:
Минимальная. 5. Функция Найденные МДНФ g 1, g 3 и МКНФ Техническая реализация минимальных форм для функции часто проще, а потому дешевле реализации ее СДНФ (СКНФ). Следовательно, этап минимизации при конструировании логических схем является одним из важнейших.
|







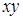





















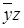
 и
и 
 есть минимальное доопределение функции f в классе КНФ.
есть минимальное доопределение функции f в классе КНФ. являются минимальными доопределениями функции f в классе нормальных форм.
являются минимальными доопределениями функции f в классе нормальных форм.


